|
Análisis
estructural: con este procedimiento se estiman las variaciones
de la Fuerza Cortante y el Momento Flector, originadas por la
geometría general del elemento, las cargas actuantes y los tipos
y localización de los apoyos. En las figuras siguientes se
muestran ejemplos de resultados de análisis estructural de
varias vigas, donde varían las cargas actuantes y los tipos de
apoyos.
Esta comparación analítica será ilustrativa de los
fenómenos que gobiernan la flexión, por lo que se deben
leer con atención.
Caso
1: Viga simplemente apoyada (Isostática)
con carga puntual en el centro de la luz.
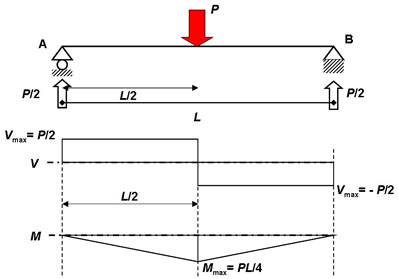
Las reacciones son idénticas, debido a la posición
simétrica de la carga respecto de los apoyos (que además
actúan de igual manera, es decir, absorbiendo cargas
verticales), recibiendo cada
una de ellas la mitad de la carga puntual.
Nótese como los diagramas son lineales en ambos casos (FC y MF), esto es
debido al tipo de carga (puntual).
El diagrama de FC
es una función lineal constante, con expresión:
V(x) = P/2
= 0,5P
hasta la mitad de la luz; de ahí en adelante y debido a la
posición y magnitud de la carga P, se produce
una discontinuidad de la función de FC, que
seguirá siendo constante pero con con signo negativo,
según la expresión:
V(x) = - P/2 = -0,5P
El diagrama de MF,
es una
función lineal discontinua por tramos, con discontinuidad en x = L/2, donde hay
un cambio de signo de la pendiente (de 0,5 a -0,5). La pendiente de la
recta
será positiva en la mitad izquierda de la viga y negativa en la
derecha, con las expresiones:
M(x) = Px/2 = 0,5Px (mitad izquierda)
M(x) = - Px/2 = - 0,5Px (mitad derecha)
En el punto de cambio de signo de la pendiente se produce un
máximo valor de la variable MF, que
será el mayor en toda la longitud de la viga AB, y tiene el valor:
|
Caso
2: Viga con empotramiento y rodillo (Hiperestática de Grado 1)
con carga puntual en el centro de
la luz.
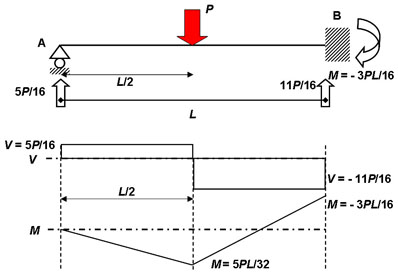
Es notable cómo al
cambiar uno de los apoyos (en este caso el empotramiento en B), las reacciones verticales no son
iguales entre sí. El empotramiento, por tener mas capacidad de
absorción de carga, toma un 68,75% de la carga total (carga
puntual en centro de luz), mientras el rodillo sólo toma un
31,25% de la carga total (menos de la mitad de lo que toma el
empotramiento).
Los diagramas son lineales, tanto para FC como para MF, pero se
diferencian del Caso 1,
en que las cantidades son diferentes. Analizando la variación de
la Fuerza Cortante, es evidente que la función constante en la
primera mitad de la viga (mitad izquierda) tiene la expresión:
V(x) = 5P/16 = 0,3125P
Esta función
constante tiene menor valor que la producida en el mismo tramo de la
viga en el Caso
1.
Al entrar en juego la carga
puntual P,
la función de la cortante tiene la expresión:
V(x) = -11P/16 = -0,6875P
El valor absoluto de la FC es mayor en
la mitad derecha de la viga, y además será también
mayor (en valor absoluto) que la función de FC en su
homólogo del Caso 1.
Con respecto al diagrama de MF, se puede
observar que el empotramiento introduce un momento negativo en el
extremo B, que será
mayor (en valor absoluto) que el momento en el centro de la luz. Sin
embargo, la diferencia entre los dos valores (absolutos) de MF no es muy
grande. Al comparar con el mayor valor absoluto de MF en la viga
del Caso 1,
es evidente que el mayor valor absoluto del Caso 2,
es una fracción de este:
[ MF1] = PL/4 = 0,25 PL
[MF2] = 3PL/16 = 0,1875PL
Donde:
[ MF1] es el máximo valor
absoluto del momento en el Caso1, y
[ MF2 ] es el máximo
valor absoluto del momento en el Caso2
De manera que:
Esto significa que el
momento flector máximo absoluto en el Caso 2
es un 25% menor que el momento flector máximo absoluto en
el Caso 1.
La conclusión inmediata de esta comparación es que:
La
inclusión de apoyos con mayores restricciones, disminuye en
momento flector máximo de una viga.
|
|
Caso 3:
Viga biempotrada (Hiperestática
de Grado 2) con
carga puntual en el centro de la luz.
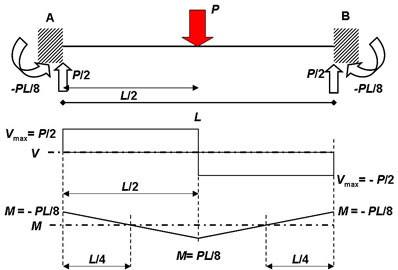
Al tener en ambos extremos
el mismo tipo de apoyo, la simetría
vuelve a la distribución de las reacciones y a los diagramas de FC y MF.
Nótese cómo las reacciones verticales son
idénticas a las del Caso 1.
Así mismo, en los empotramiento en A y B,
existen sendos momentos reaccionantes de igual magnitud.
El diagrama de FC
será idéntico al del Caso 1.
Por otro lado, el diagrama de MF es algo
distinto, pues aunque mantiene la misma forma, es decir,
idénticas pendientes para cada tramo, con punto de
discontinuidad en x
= L/2, el
diagrama se ha desplazado sobre el eje de M = 0 (hacia
arriba), una distancia igual a la magnitud del momento en los extremos,
es decir, PL/8.
Si comparamos estos valores con aquellos del Caso 2,
es notable que los valores máximos (absolutos) del momento son
menores. Aplicando relaciones similares a las del Caso2,
tenemos:
[MF2] = 3PL/16 = 0,1875PL
[MF3] = PL/8 = 0,125PL
Donde:
[MF2] es el máximo valor
absoluto del momento en el Caso2, y
[MF3] es
el máximo valor absoluto del momento en el Caso3
De manera que:
[MF3] = 0,6667[MF2]
Esto significa que el
momento flector máximo absoluto en el Caso 3
es una tercera parte menor que el momento flector máximo
absoluto en el Caso 2.
La conclusión inmediata de esta comparación es nuevamente:
La
inclusión de apoyos con mayores restricciones, disminuye en
momento flector máximo de una viga.
|
TABLA 1:COMPARATIVA DE LOS MÁXIMOS
VALORES ABSOLUTOS DE MF PARA LOS CASOS 1, 2 Y 3
Casos
|
[MFN]
|
[MFN]/[MF1] |
Caso 1
|
0,25PL
|
1
|
| Caso 2 |
0,1875PL |
0,75
|
| Caso 3 |
0,125PL |
0,5
|
En la TABLA 1 se presentan los valores
máximos absolutos de Momento Flector para cada uno de los casos,
y en la columna de la extrema derecha, la relación normalizada
de los momentos flectores con respecto al máximo valor absoluto
del Caso 1.
Queda claro entonces, que los tipos de apoyo juegan un papel importante
en la variación del momento flector a lo largo de una viga.
Así mismo, la
inclusión de apoyos tipo empotramiento reducen considerablemente
los máximos valores absolutos de momento flector en una viga.
Podemos ver entonces cómo el máximo valor absoluto de MF en el Caso 2
es un 75% de aquel del Caso 1:
[MF2]/[MF1] = 0,75
y el del Caso
3 un 50%:
[MF3]/[MF1] = 0,5
|
|
Caso 4:
Viga simplemente
apoyada con carga uniformemente distribuida.
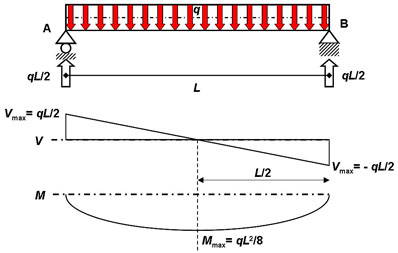
En este caso, al igual que en el Caso 1
las reacciones, así como los diagramas de FC y MF presentan
simetrías, es decir, las reacciones verticales son
idénticas en A y en B (ya que los apoyos reaccionan de
igual manera, es decir, absorbiendo cargas
verticales), en el diagrama de FC se verifica
una simetría central respecto de un punto en el centro de la luz
de la viga, y en el de MF una
simetría respecto de un eje vertical por el centro de la luz de
la viga.
Las funciones de FC
y MF son,
respectivamente, lineal (de primer grado) y cuadrática (de
segundo grado). Dichas funciones tienen la forma:
V(x) = qL/2 - qx (Fuerza
Cortante)
M(x)
= qLx/2 - qx2/2
(Momento Flector)
Es importante hacer notar que la FC tiene dos
máximos absolutos: en A
y en B, mientras que el MF sólo
tiene un máximo en el centro de la luz.
|
Caso 5:
Viga con
empotramiento y rodillo con carga uniformemente distribuida.
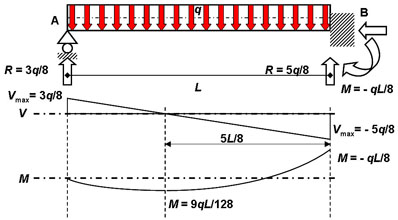
Las reacciones verticales no
serán idénticas puesto que el
empotramiento tiene la capacidad de tomar más carga que el
rodillo, se
verifica entonces como el apoyo en B
reacciona tomando 62,5% de la carga total sobre la viga, mientras el
apoyo en A toma un 37,5%. Al
comparar con las reacciones del Caso 4,
es notable como la reacción en B
es mayor que la de su homóloga y la reacción en A es menor. Además se debe
tener en cuenta que por el empotramiento en B se genera una reacción en
forma de momento.
Vemos nuevamente (similar al Caso 2)
cómo la introducción de un empotramieno (en el extremo B de la viga) induce
asimetría en los diagramas de FC y MF.
Los máximos valores absolutos de FC y MF se encuentran
en el extremo B
(empotramiento),
|
Caso 6:
Viga biempotrada
con carga uniformemente distribuida.
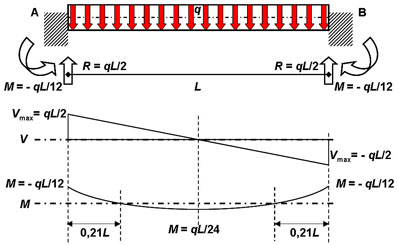
Al tener en ambos extremos
el mismo tipo de apoyo, la simetría
vuelve a la distribución de las reacciones y a los diagramas de FC y MF.
Nótese cómo las reacciones verticales son
idénticas a las del Caso 4.
Así mismo, en los empotramiento en A y B,
existen sendos momentos reaccionantes de igual magnitud.
El diagrama de FC
será idéntico al del Caso 4.
Por otro lado, el diagrama de MF es algo
distinto, pues aunque mantiene la misma forma, el
diagrama se ha desplazado sobre el eje de M = 0 (hacia
arriba), una distancia igual a la magnitud del momento en los extremos,
es decir, QL/12.
Si comparamos estos valores con aquellos de los Casos 4 y 5,
es notable que los valores máximos (absolutos) del momento (en
esta viga: Caso
6) son
menores. Aplicando relaciones similares a las del Caso 5,
tenemos:
[MF5] = qL/8 = 0,125qL
[MF6] = qL/12 = 0,0833qL
Donde:
[MF5] es el máximo valor
absoluto del momento en el Caso 5,
y
[MF6] es
el máximo valor absoluto del momento en el Caso 6
De manera que:
[MF6] = 0,6667[MF5]
Esto significa que el
momento flector máximo absoluto en el Caso 6
es una tercera parte menor que el momento flector máximo
absoluto en el Caso 5.
La conclusión inmediata de esta comparación es nuevamente:
La
inclusión de apoyos con mayores restricciones, disminuye en
momento flector máximo de una viga.
|
|
|

