Matrices: Una generalización del concepto de tablero.

Una vez que hemos desarrollado el concepto de tablero, pasemos a trabajar con las matrices, lo cual es una generalización de todo lo anterior. Es decir, la información relevante en nuestro problema eran los números y sus ubicaciones dentro de unos tableros. Podemos simplificar mucho más las cosas, si dejamos de lado, los colores, iconos, nombres de materiales, casas,...,etc, para concentrarnos en los cálculos. Lo que nos interesa es la matemática que hay detrás de los tableros y sus relaciones . Por eso  vamos a adoptar unos símbolos mucho más sencillos y económicos , que tengan las mismas propiedades de los tableros. Este nuevo modelo será definitivo en cuanto al desarrollo de este tema.

El  tablero de la sala  los representamos por una matriz de tres filas por tres columnas.

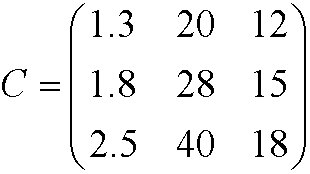
o tal vez vale la pena usar matrices coloreadas.

☺Es más divertido usar colores....

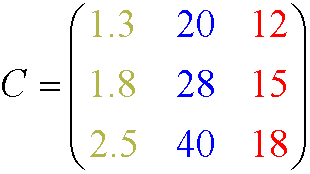
p¡¡¡¡ Cuidado!!!

Antes de avanzar, debemos dar algunas definiciones....

1) Una matriz de orden nxm con coeficientes reales  es un arreglo rectangular de números reales de la forma

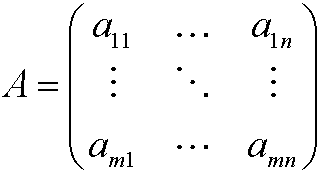
los números a _{i j}  son los elementos o entradas de la matriz. El primer subindice indica la fila a la cual pertenece y el segundo la posición dentro de la fila o la columna donde está. La matriz anterior tiene m filas y n columnas.

2) Una matriz fila es aquella compuesta de una sola fila. Por ejemplo

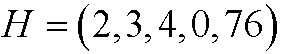
3) Una matriz columna es aquella compuesta de una sola columna. Ejemplo.

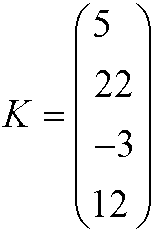
4) Una matriz cuadrada es aquella que tiene el mismo número de filas y columnas. Ejemplo

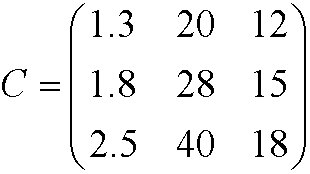
5) La diagonal de una matriz cuadrada está formada por los elementos que están sobre la diagonal del cuadrado . Es decir su posición dentro de una fila es igual al número de la fila. La diagonal de la matriz anterior son los elementos 1.3, 28 y 18.