Determinantes.

Supongamos que tenemos una matriz cuadrada A de tamaño 3x3 ( esto es, 3 filas por tres columnas ). Entonces podemos simplificar un poco las cosas, olvidarnos del valor de cada coeficiente y pensar solamente en la posición que ocupan dentro de la matriz. Los elementos de la primera fila son amarillos, los de la segunda fila azules y los de la tercera fila rojo. Así pues tendremos una matriz tricolor

supongamos que, por alguna razón expuesta más adelante,  queremos realizar todos los posibles productos de tres elementos de la matriz, con la siguiente condición

1. No se pueden repetir elementos
2. Cada elemento pertenece a una fila diferente.
3. Cada elemento pertenece a una columna diferente.

¿ Cuántas posibilidades tendremos?

Observa los seis productos de abajo.

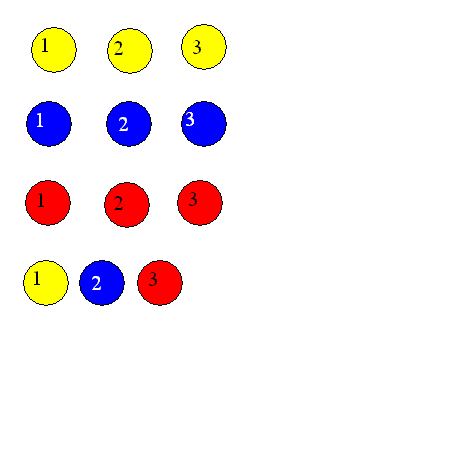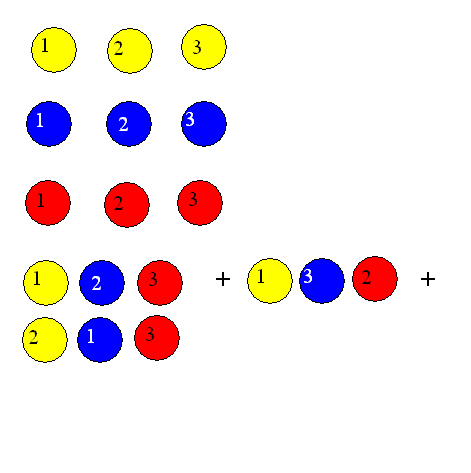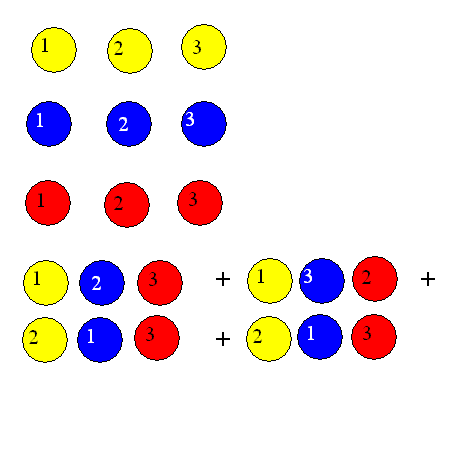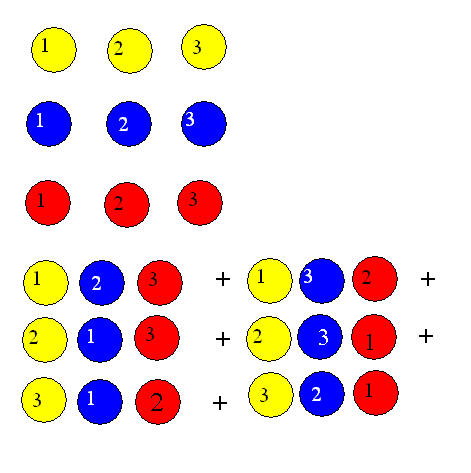
 Cada uno de estos productos posee un signo especial que depende de la permutación de los números 1, 2 y 3. Unos productos serán positivos y otros negativos. Estudiaremos cada una de ellas en detalle y determinaremos su signo. El signo viene dado por el número de transposiciones necesarias para obtener la secuencia original 1 2 3. Cada transposición no es más que un intercambio de alguna pareja, entre los números 1, 2 y 3.

La permutación de abajo es igual a una transposición.

¿Cuál es el signo de una transposición?

Una transposición tiene signo menos.

Dicho de otra forma : Toda transposición es un permutación impar.

La permutación de abajo es la composición de dos transposiciones.

El producto de dos transposiciones tiene signo mas.

Dicho de otra manera: El producto de dos transposiciones es una permutación par.

La permutación identidad deja la secuencia 1,2, 3 igual  ¿ Cuál es el signo de la permutación identidad ?

La permutación identidad tiene signo mas.

Entonces el determinante de la matriz 3x3 que teníamos al inicio, es igual a la suma de todos los productos considerados arriba con el signo dado por la permutación correspondiente. Luego

Podemos hacernos varias preguntas:

1. ¿ Qué pasa si en la matriz se multiplican todos los elementos de una fila , por ejemplo la fila amarilla, por una constante ? ¿ Cómo queda el determinante ?

2. ¿ qué pasa si en una fila, cada elemento es la suma de dos términos ? ¿ cómo se expresa el determinante ?

3. ¿ Es el determinante una función lineal de las filas?

4. ¿ Qué pasa si una fila tiene todos sus elementos iguales a cero?

5. ¿Que pasa si dos filas son iguales? Por ejemplo, lo que ves ahora rojo se hace azul. ¿ cuanto vale el determinante?

6. ¿ que pasa si tomamos la matriz transpuesta de A ? ¿ Cambiará el valor del determinante ?