Imaginémonos que somos seres de otra galaxia y  vivimos dentro de un mundo unidimensional, inmersos dentro de una línea continua.

 -¿ Qué diferencia hay entre una línea recta y una línea curva ?- Pregunta el profesor.

- Por supuesto que son muchas- responde una estudiante de nombre Luisa. Por ejemplo, cuando recorremos la línea recta siempre lo hacemos en la misma dirección. En una línea curva, por el contrario, cambiamos varias veces de dirección al recorrerla.

- Muy bien - dice el profesor- Pero debo decirte Luisa, que tu observación viene de una persona del mundo tridimensional. En un mundo de una dimensión, solo hay dos direcciones: hacia adelante o hacia atrás.

- La línea curva puede ser más larga que la recta - interviene Pedro.

-Correcto Pedro, pero recordemos que la longitud es un concepto métrico y no topológico. Yo puedo rehacer la curva de nuevo, más pequeña de manera que tenga la misma longitud que la recta y todo arreglado. ¿Qué sucede entonces?

- La verdad es que no conozco mucho de mundos unidimensionales- responde Pedro.

- Veamos otras posibilidades de  M.G.U. (mundos galácticos Unidimensionales). Ahora hay cuatro mundos distintos en apariencia: los mundos A, B, C Y D ¿ Qué diferencia hay entre ellos?

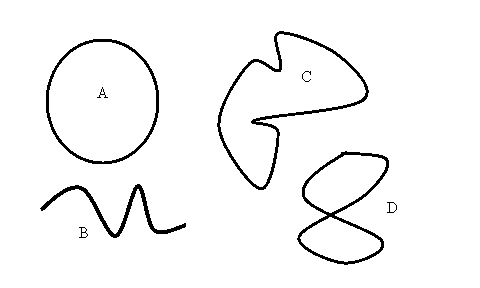
-El mudo A es cerrado- Interviene Luisa- es decir, si viajamos desde un punto cualquiera hacia adelante, en algún momento volveremos al punto inicial, sin necesidad de devolvernos.

- El mundo B no es cerrado- Agrega Hermes - Si iniciamos un viaje en un punto cualquiera, para retornar al punto de salida, debemos cambiar de dirección: es decir devolvernos hacia atrás.

- El mundo C es casi la misma cosa que el mundo A - dice Pedro. Se podría decir que A y B son mundos equivalentes.

-El mundo D tiene algo muy especial - agrega otro estudiante de nombre Arquímedes- Si iniciamos un viaje de circunvalación en un punto cualquiera alrededor del mundo D, pasaremos dos veces por el mismo punto de corte. Por lo tanto el mundo D es diferente de los tres anteriores.

-Todas las observaciones son correctas- dice el profesor. Veamos ahora como la topología puede ayudarnos a establecer estas diferencias. Usaremos un concepto que será fundamenta: el de Homeomorfismo.

Una propiedad de un espacio métrico M se dice que es una propiedad topológica cuando es invariante bajo homeomorfismos. Esto es, todo espacio N homeomorfo a M, goza de la misma propiedad.

Es claro que la relación de homeomorfismo entre los espacios métricos es una relación de equivalencia. La demostración de este hecho se deja como un ejercicio.

Ejemplo1. En la recta real, todos los intervalos abiertos son homeomorfos. Para ver esto, sea I = ( a, b) y  probaremos que es homeomorfo al intervalo (0, 1). La aplicación

f : (0, 1) ———→ ( a, b),   f( x) = ( b -a) x + a es biyectiva, lineal y por lo tanto continua. Además su inversa también es continua. Luego (a, b) es homeomorfo a ( 0, 1).

Ejemplo 2. En un espacio métrico normado ( M, ||  || ), todas las bolas abiertas son homeomorfas. Para demostrar este hecho, consideremos las aplicaciones t _a : M ———→ M ,  t _a ( x) = x + a ,llamada translación y  h _m : M ———→ M , h _m ( x) =  m. x , llamada la homotecia, las cuales son homeomorfismos. Si B ( a, r ) y B ( b, s) son dos bolas abiertas, entonces la aplicación

φ =  t _b o  h _s/r  o t _-a   es un homeomorfismo y envía B (a, r) en B (b, s).

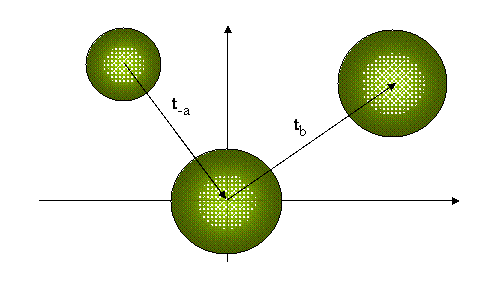
El efecto de aplicar φ, es el siguiente: en primer lugar, trasladamos la primera bola hasta el origen, luego le aplicamos la homotecia para tener una bola del mismo tamaño de la segunda. Finalmente, trasladamos esta bola hasta la posición de la segunda.

Ejemplo2. La condición de espacio discreto es una propiedad topológica.  En efecto, si M es discreto y f es un homeomorfismo entre M y otro espacio métrico N, entonces N debe ser discreto. Sea a un punto de N, como f es biyectiva existe un único punto x en M tal que f (x) = a.

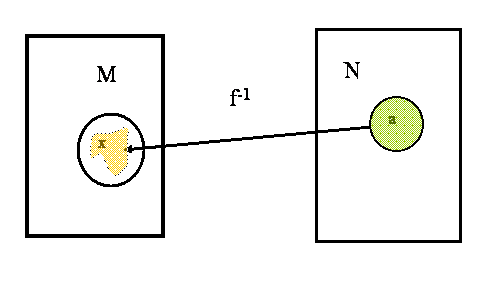
Como M es discreto el punto x es un punto aislado y podemos tomar una bola B con centro en x que no contenga ningún punto de M. Por la continuidad de f ^-1, debe existir un  δ > 0, y una bola B´ (de color verde) centrada en a  y de radio δ , tal que la imagen bajo f ^-1 de bola B´ ( de color amarillo) , cae dentro de la bola B. Luego en B´ no hay puntos de N distintos de a. ¿Porqué? Esto demuestra que el punto a es aislado y por lo tanto el espacio N es discreto.

Ejemplo 3. Inmersiones topológicas . Una  aplicación inyectiva f : M ——→ N la cual es un homeomorfismo sobre su imagen se llama un inmersión topológica. Por ejemplo las curvas del plano, dadas en forma paramétrica  r: I ———→ R² ,  r( t) = ( t , f( t)) con f continua.

Ejemplo 4. Una línea curva puede ser homemorfa a una línea recta. Consideremos la inmersión  f : R ———→ C Í R² , f (t) = ( t, sen t ) , la cual envía a toda la recta real en la curva sinusoidal del plano. Es claro que f es biyectiva y continua, siendo su inversa la función proyección P (x, y) = x, la cual es continua. En la animación vemos como se va generando esta curva a medida que el parámetro t va recorriendo la recta real.

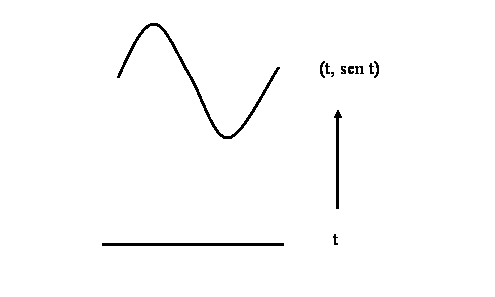
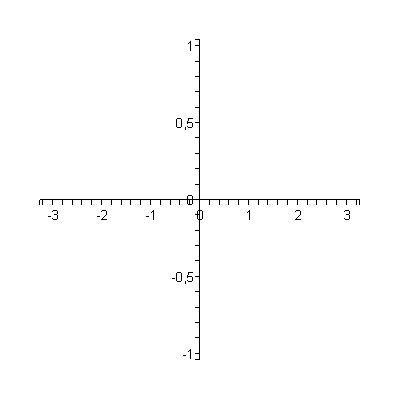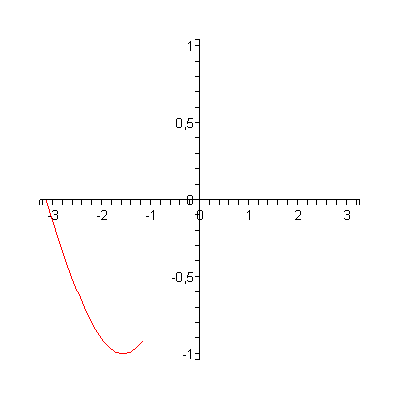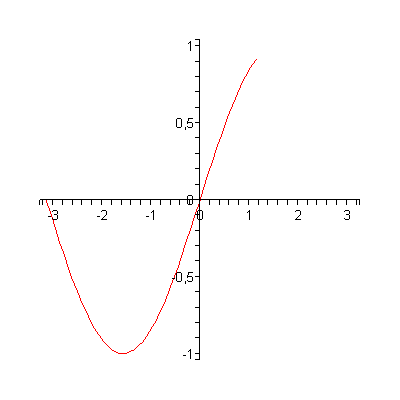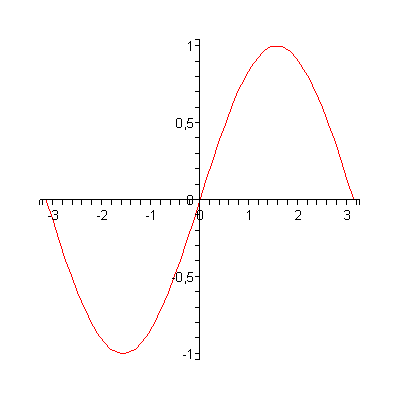
Ejemplo 5. Una biyección continua entre un segmento de recta y la circunferencia, la cual no es un homeomorfismo. Consideremos la parametrización de la circunferencia

S = { (x, y ) Π R² /  x ² +  y ²   =  1 }

dada por la función  f : [ 0, 2π ) ———→  S, f( t) = ( sen t, cos t ) .

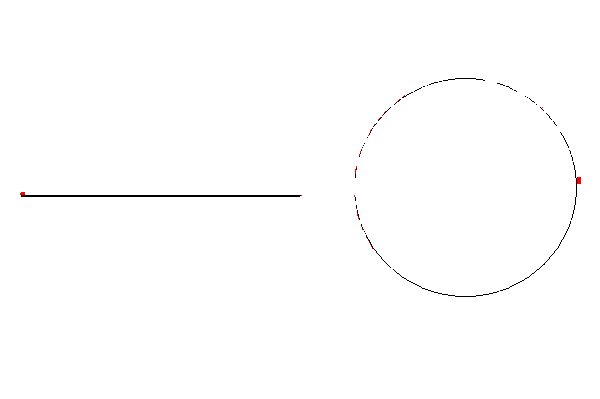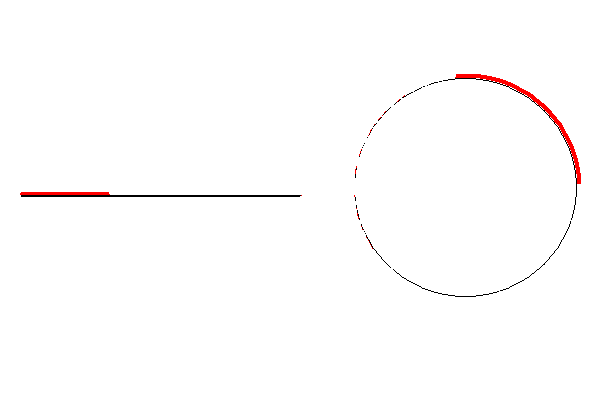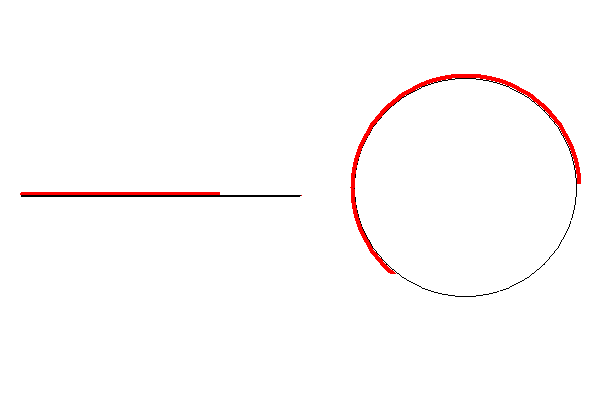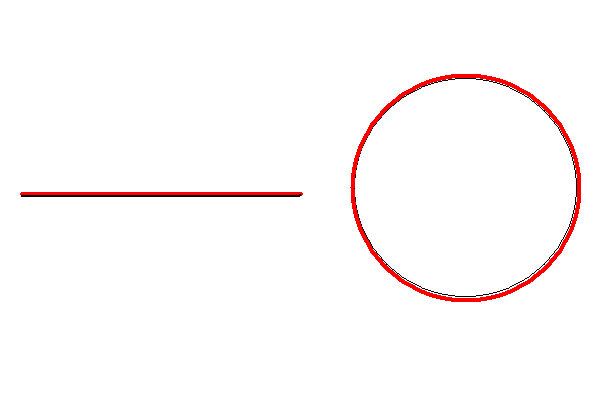
Es claro que f es una biyección y además continua. Pero su inversa no es continua.

Si tomamos una bola con centro en el punto P ( 0, 1) de radio 1/2 entonces las imágenes bajo f ^-1, de puntos dentro de esta bola están bastante separadas: una parte está cercana a  0, y la otra a 2 π.

Por lo tanto  f ^-1, no puede ser continua y así f no es un homeomorfismo. Por supuesto que esta no es una demostración de que S y el segmento no son homeomorfos. Más adelante, cuando estudiemos el concepto de conexidad, probaremos que ellos no pueden ser homeomorfos.

Página Principal               Siguiente Ü