Capítulo 5

Estudiaremos en este capítulo uno de los conceptos básicos de la topología como lo es el de compacidad. La motivación proviene de uno de los espacios métricos más estudiados por los matemáticos: los números reales.  Los conjuntos cerrados y acotados de la recta real poseen una serie de propiedades interesantes que se traducen en resultados de mucha utilidad en el análisis clásico. Algunos de estos resultados son los siguientes

1) Teorema de Bolzano - Weierstrass- Toda sucesión infinita de números reales dentro de un conjunto cerrado y acotado, posee una subsucesión convergente.

2)Teorema de máximos y mínimos de Weierstrass -  Toda función continua definida sobre un intervalo cerrado y acotado, alcanza un máximo y un mínimo.

3) Teorema fundamental del álgebra- Todo polinomio con coeficientes reales posee una raíz compleja.

4) Teorema de aproximación de funciones de Stone- Weierstrass- Toda función continua f , definida sobre un intervalo [ a, b] se puede aproximar uniformemente mediante una sucesión de funciones polinomiales. Es decir, existe una sucesión de polinomios { P _n  } tal que

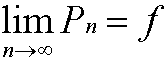
Comenzaremos nuestra exposición, dando la definición fundamental de este capítulo.

La definición de compacidad, se puede extender a subconjuntos de M de la siguiente forma:  Un subconjunto A de M se dice compacto, cuando considerado como espacio métrico en sí mismo, con la métrica inducida por d, la métrica de M, es compacto.

Ejemplo1. Todo conjunto cerrado y acotado de números reales es compacto.

En efecto, sea A un conjunto cerrado y acotado y { x _n } una sucesión de elementos de A. Entonces, como A es acotado, la sucesión es acotada y por lo tanto posee una subsucesión  { x _φ(n) }convergente a un número real x ₀. Es claro que  x ₀ es un punto de acumulación de A y siendo A cerrado, se tiene que x ₀ pertenece a A. Luego la sucesión dada posee una subsucesión convergente en A y por lo tanto A es compacto.

Ejemplo 2. Todo conjunto finito de puntos, con la métrica discreta,  es un espacio métrico compacto.

Ejemplo 3. El conjunto de los números reales R, con la métrica usual ( euclideana) no es compacto.

Basta ver que la sucesión de  los números naturales, no posee subsucesión convergente en R.

Veremos ahora algunas definiciones de compacidad, que no dependen de sucesiones.

Los conjuntos compactos se pueden ver en forma intuitiva como la unión de conjuntos muy pequeños.

Definición . Sea ( M, d) un espacio métrico. Un subconjunto no vacío A de M se llama Precompacto, si para cada  ε > 0 , existen subconjuntos no vacíos A₁ , ...., A _n   tales que la unión de todos ellos es A,  y además, el diámetro de cada uno de ellos es menor  o iguala a ε.

ES un ejercicio muy sencillo, demostrar que todo conjunto compacto es precompacto.

La siguiente proposición la dejamos como un ejercicio para el lector.

Proposición  Un subconjunto A de un espacio métrico M es precompacto, sí y sólo si para cada  ε > 0, existe un conjunto finito de puntos de A, denotado por  S_ε = { a₁ , ....., a _n } tal que

A Ô  D (  a₁ ,  ε) ∪ ....∪ D (  a _n ,  ε),

donde D ( a _i ,  ε) denota el disco cerrado de centro en   a _i  , y radio ε .

El siguiente teorema o definición alternativa de compacto se puede consultar en la bibliografía.

El Teorema de Heine- Borel

Definición . Sea X un espacio métrico. Un cubrimiento abierto de X es una familia ℬ,  de conjuntos abiertos tal que X está contenido en la unión de todos ellos.

Ejemplo: Sea X = R² , el espacio real Euclideano bidimensional  y ε un número real cualquiera. Entonces el conjunto

ℬ = { B ( x, ε) / x punto de  R²  }

es un cubrimiento abierto.

Antes de estudiar el Teorema H-B, necesitamos el siguiente resultado

Proposición ( Propiedad de Lebesgue) Sea U un cubrimiento abierto de un espacio compacto X. Entonces existe ε > 0 , con la siguiente propiedad:  Para cada x en X, existe un abierto U _x , tal que B ( x, ε ) Ô   U _x  .

Para la demostración, supongamos por el absurdo, que para cada  ε > 0, existe un x en X, denotado por x(ε ) tal que B ( x, ε )  no está contenida en ningún abierto de U. Entonces podemos formar una sucesión { x _n }en X, tal que  B( x _n , 1/ n) no está contenida en ningún abierto de U. Como X es compacto, la sucesión posee una subsucesión convergente a  x₀  ∈X. Como U es un cubrimiento de X, existe un abierto en U en U, tal que  B ( x ₀  , r ) Ì  U. Si tomamos un N natural que  1 / N < r / 2, y d ( x _N, x ₀) < r / 2, entonces probaremos que B ( x _N , 1 / N ) Ì U , lo cual es una contradicción.

En efecto, si x ∈ B ( x _N , 1 / N ), entonces

d ( x, x ₀   )  ≤ d ( x, x _N ) + d ( x _N, x ₀) < 1 / N + r / 2 <  r.

Luego x  ∈ B ( x ₀  , r ) Ì  U.

Con esto termina la demostración.

Demostración:

Página Principal