Algebra Lineal en MAPLE
Luis A. Núñez
Centro de Astrofísica Teórica,
Departamento de Física, Facultad de Ciencias,
Universidad de Los Andes, Mérida 5101, Venezuela y,
Centro Nacional de Cálculo Científico, Universidad de Los Andes (CECALCULA),
Corporación Parque Tecnológico de Mérida, Mérida 5101, Venezuel
a
e-mail: nunez@ula.ve
actualizado: Mayo 2004
Antes de comenzar a calcular cualquier cosa con vectores y matrices es recomendable (casi indispensable) incorporar la biblioteca de comandos de álgebra lineal, en la mayor parte de los textos y los paquetes aprece reportado el uso de la biblioteca with(linalg) a partir de MAPLE 6 se consideró obsoleto y fue sustituda por la biblioteca LinearAlgebra sto es
| > | restart:with(LinearAlgebra); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Los nombres de los comandos son sugerentes y utilizaremos algunos de ellos, siempre se puede encontrar una descripción (en inglés) de un comando específico mediante ?comando o se puede explorar la sintaxis y el significado de los comandos en la ayuda de MAPLE
Mathematics -> Linear Algebra -> Linear Algebra Package -> Standart -> comando
| > | ?Matrix |
veamos algunos elementos de la sintaxis.
Hay varias de identificar una matriz en MAPLE, la primera y la más antigua es
| > | A := Matrix([[a[11], a[12], a[13]], [a[21], a[22], a[23]], [a[31], a[32], a[33]]]); |

y
| > | B := Matrix([[b[11], b[12], b[13]], [b[21], b[22], b[23]], [b[31], b[32], b[33]]]); |
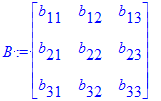
a partir de aquí podemos identificar la matriz y realizar un conjnto de operaciones, las cuales resultan bien intuitivas.
si dos matrices
A
y
B
de orden
(
![]() ×
×
![]() )
con elementos,
)
con elementos,
![]() y
y
![]() ,
respectivamente, su suma
A
+
B
será la matriz
C
también de orden
(
,
respectivamente, su suma
A
+
B
será la matriz
C
también de orden
(
![]() ×
×
![]() )
con elementos
)
con elementos
![]() los cuales se obtienen al sumar elementos con los mismos índices, vale decir
los cuales se obtienen al sumar elementos con los mismos índices, vale decir
![]()
De la misma manera se pueden construir: resta de matrices, multiplicaciones de escalares por matrices, y suma de escalares y matrices, veamos:
| > | `B + A`= B + A; `9A - 18B` = A.9 - B.18; `A + 7.7` = A + 7.7; `A . 2.7` = A . 2.7; |
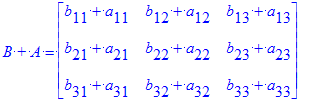
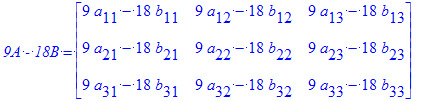
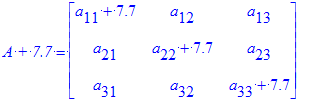

como ejercicio, pruebe que la suma de matrices es conmutativa y asociativa
A
+
B
=
B
+
A
(
A
+
B
) +
C
=
A
+ (
B
+
C
)
Por su parte la multiplicación de dos matrices
A
de orden
(
![]() ×
×
![]() )
con elementos
)
con elementos
![]() y
B
de orden
(
y
B
de orden
(
![]() ×
×
![]() )
con elemetos
)
con elemetos
![]() ,
entonces la matriz producto
,
entonces la matriz producto
A
B
será una matriz
C
de orden
(
![]() ×
×
![]() )
representada por elementos
)
representada por elementos
![]() tales que los elementos
tales que los elementos
![]() + ... +
+ ... +
![a[ip]*b[pj] = Sum(a[ik]*b[kj],k = 1 .. p)](images/AlgebraLinealLN38.gif) i
= 1,...,
m
;
j
= 1,...,
p
i
= 1,...,
m
;
j
= 1,...,
p
o utilizando la convención de Einstein en la cual índices repetidos indical suma
![]() =
=
![]()
Así la multiplicación de matrices y la potencia de matrices será
| > | `A B`:=A . B; `B A`:=B . A; |
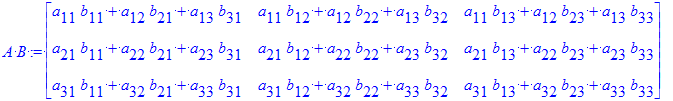
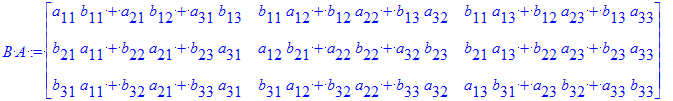
Existen otras sintaxis menos intuirtivas las cuales invocan a subrutinas internas de la biblioteca de LinearAlgebra y son mucho más eficientes. Estas sintaxis se recomiendan para problemas que contemplen cómputos significativos
| > | MatrixAdd( B, A ); MatrixAdd( A, B, 9, -18 ); MatrixMatrixMultiply(A,B); ScalarMultiply( A, 2.7 ); |
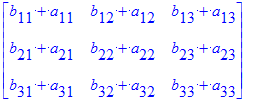
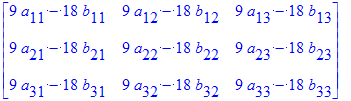
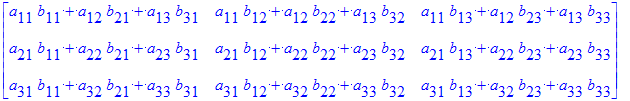

un caso más ilustrativo que muestra otra importante propiedad (la traspuesta) de las matrices y que se intuye por el nombre del comando es
| > | R := Matrix([[cos(theta),-sin(theta)],[sin(theta),cos(theta)]]); |
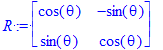
| > | MatrixMatrixMultiply(R, Transpose(R)); |
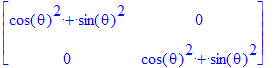
| > | Map(simplify,%); |
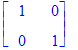
también se puede hacer operaciones dentro de la matrices y avanzar en su sintaxis
| > | m := Matrix(2,3,(i,j)->i+j); n := Matrix(2,2,fill=Pi); |
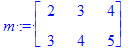
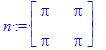
Las matrices pueden tener valores numéricos
| > | P := Matrix( [[1,2,3],[3,1,2],[2,3,1]] ); Q := Matrix( [[5,14,3],[3,2,1],[1,12,3]] ); |
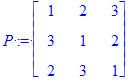
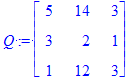
por lo tanto el conmutador [ P,Q ] = PQ - PQ podemos expresarlo como
| > | `[P,Q]`=(P . Q) - (Q . P); |
![`[P,Q]` = Matrix(%id = 787308)](images/AlgebraLinealLN54.gif)
con lo cual es claro que, en general, la multiplicación de matrices no es conmutativa, es decir [ A,B ] = AB - BA , en general no se anula. sin embargo hay ocasiones en que si
| > | M1 := Matrix(2, 2, [[6, 8],[4, 6]]); M2 := Matrix(2, 2, [[15, 20], [10, 15]]); `[M1,M2]`= M1 . M2 - M2 . M1; |
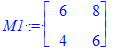
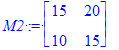
![`[M1,M2]` = Matrix(%id = 1016060)](images/AlgebraLinealLN57.gif)
Otro punto importante es que el producto de dos matrices que sea cero no implica que algunas de las matrices lo es
| > | AA := Matrix(3, 3, [[1, -1, 1], [-3, 2, -1], [-2, 1, 0]]); BB := Matrix(3, 3, [[1, 2, 3], [2, 4, 6], [1, 2, 3]]); |
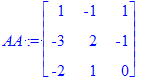
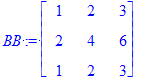
| > | AA . BB; |
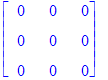
pero
| > | BB . AA; |
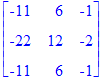
Compruebe que la multiplicaci'on de matrices es asociativa
A ( B C ) = ( A B ) C
( A B ) C = A ( B C )
y distributiva respecto a la suma de matrices
A ( B + C ) = A B + A C
(B + C ) A = B A + C A
( A + B ) ( M + N ) = A ( M + N ) + B ( M + N )
Finalmente las potencias de matrices
| > | `B^2`=B ^ 2; `B B`=B . B; |
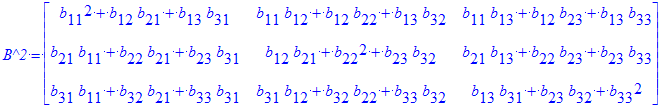
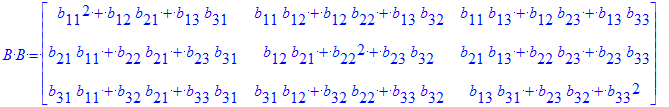
Valen potencias negarivas
| > | P ^ (-2); |

O tambi'en
| > | MatrixPower(B,2); MatrixPower(P,-2); |
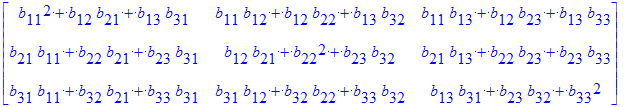

Urgando entre los nombres de los comandos de bibliotecas que aparecen al invocarla algunos sugieren (y son) el c'alculo de propiedades de matrices:
La diagonal
| > | Diagonal(P); |
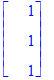
La Traza
| > | TrazaP:=Trace(P); |
![]()
El Determinante
| > | `det(P)`=Determinant( P ); |
![]()
con lo cual es claro que
| > | `det(P)`:=Determinant(P);`det(Q)`:=Determinant(Q);`P Q`=P . Q;`det(PQ)`:=Determinant(P . Q); |
![]()
![]()
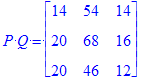
![]()
N'otese que para el caso de las matrices AA y BB el determinante de BB se anula, por lo tanto det( AB ) = det( A ) det( B ) = det( BA ) = 0
| > | Determinant( BB ); |
![]()
| > | Determinant( AA . BB ); Determinant( BB . AA ); |
![]()
![]()
y Matricea que tengan una fila, una columna nula o dos filas iguales, tendr'an nulo su determinante
| > | A01 := Matrix(3, 3, [[a0[11], a0[12], a0[13]], [ 0, 0, 0], [a0[31], a0[32], a0[33]]]); A02 := Matrix(3, 3, [[a0[11], 0, a0[13]], [ a0[21], 0, a0[23]], [a0[31], 0, a0[33]]]); A03 := Matrix(3, 3, [[a0[11], a0[11], a0[11]], [a0[11], a0[11], a0[11]], [a0[31], a0[32], a0[33]]]); `det(A01)`=Determinant(A01); `det(A02)`=Determinant(A02); `det(A03)`=Determinant(A03); |
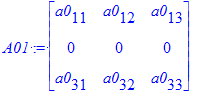
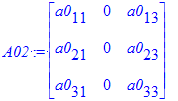
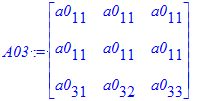
![]()
![]()
![]()
La matriz adjunta de P
| > | Adjoint(P); |
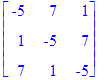
con lo cual
| > | P . Adjoint(P); |

la matriz inversa
| > | MatrixInverse(P); |

y claramente
| > | P . MatrixInverse(P); |
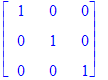
La Traspuesta conjungada o Matriz Herm'itica
| > | A1 := <<I,5,w>|<2,6*I,x>|<3 + 5*I,7,y>|<4,8 -I,z>>; HermitianTranspose(A1); |
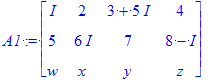
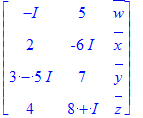
N'otese
1) Otra sintaxis para introducir matrices.
2) La barras arriba de las cantidades simb'olicas (distintas de n'umero) representan el complejo conjugado
3) El I representa el n'umero imaginario ra'iz de -1
Igualmente existe, predefinido, un zool'ogico de matrices
Identidad
| > | IdentityMatrix(4); # matriz 4 x 4 IdentityMatrix(5,4); # matriz 5 x 4 |


La matriz de Hilbert
| > | H:=HilbertMatrix(4); |
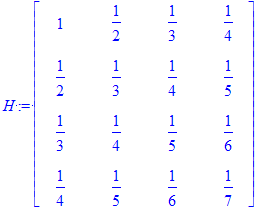
Es f'acil darse cuenta que los elementos de la matriz son
![h[i,j] = 1/(i+j-1)](images/AlgebraLinealLN92.gif) Pero la matriz de Hilbert puede ser menos intuitiva
Pero la matriz de Hilbert puede ser menos intuitiva
| > | H1:=HilbertMatrix(3, 5, x); |
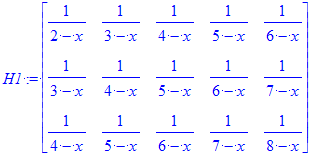
Trate de intuir el elemento de matriz
![]()
La matriz de Vandermonde
| > | VandermondeMatrix(<a,b,c,d>); |
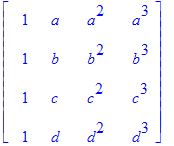
Se pueden construir tipos particulares de matrices, como las llamadas matrices en banda
| > | LL := [ [w,w,w],[x,x,x,x],[y,y,y] ]; BandMatrix(LL); |
Pero tambi'en matrices en banda de regular tamaño, por ejemplo 100x100
| > | N := BandMatrix( [-1,2,-3], 1, 100 ); |

| > | N[47,47]; N[47,48]; N[47,49]; |
![]()
![]()
![]()
Antes de continuar con la construcción de otros objetos, quisiera hacer una prueba que constituye el mayor de los avances de este paquete de subrutinas de la biblioteca de LinearAlgebra colóquese sobre la matriz de su interés. Haga clic con el botón derecho del ratón y luego presione el botón izquierdo y vea las operaciones que surgen.....
Si lo hace sobre la matriz en banda anterior y algo como esto le debe aparecer
![[Maple Bitmap]](images/AlgebraLinealLN100.gif)
Explore la figura que representa la matriz, presione el botón derecho del ratón y haga zoom
Explore adem'as las siguientes matrices 50 x 50 triangulares
| > | RandomMatrix(50,50,generator=1..9,outputoptions=[shape=triangular[lower]]); |

| > | RandomMatrix(50,50,generator=1..9,outputoptions=[shape=triangular[upper]]); |

También se pueden importar matrices de datos desde archivos Uno de los estándares de matrices m'as conocidos est'a en http://math.nist.gov/MatrixMarket/
| > | Mimport:=ImportMatrix("c:/Luisn/Latex/cursos/visualizacion/bcsstk04.mtx", source=MatrixMarket); |

Los vectores pueden ser definidos como
| > | v := <x,y,z,1>; v1 := Vector([s[1],s[2],s[3],s[4]]); v2 := Vector( [5.05, 6.125, 2.980] ); |
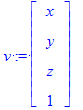
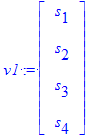
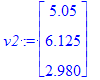
Note que las componentes de los vectores est'an almacenadas en una estrutura de datos tipo arreglo
| > | v[1];v[2];v[3];v[4];v2[1];v2[2];v2[3]; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
y las formas diferenciales
| > | u := <1|0|0|2>; u1 := Vector[row]([t[1],t[2],t[3],t[4]]); u2 := Vector[row]([9.05, 7.125, 4.980] ); |
![]()
![]()
![]()
La formas diferenciales o vectores fila, también se puede rellenar una matriz
| > | M := <<5,0,0,0>|<0,1,0,0>|<0,0,2,0>|<0,0,0,1>>; |
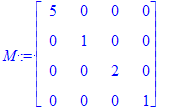
así la multiplicación de matrices y vectores o formas y matrices puede expresarse de las dos formas acostumbradas
| > | u . M; M . v; MatrixVectorMultiply(M,v); VectorMatrixMultiply(u,M); |
![]()
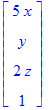
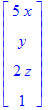
![]()
y el producto interno o escalar de dos vectores ser'a
| > | u . v; u1 . v1; DotProduct(u,v); |
![]()
![]()
![]()
| > | CrossProduct(u2,v2); |
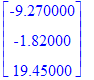
| > |
| > |