Visualización y Simulaciones en MAPLE
Luis A. Núñez
Centro de Astrofísica Teórica,
Departamento de Física, Facultad de Ciencias,
Universidad de Los Andes, Mérida 5101, Venezuela y,
Centro Nacional de Cálculo Científico, Universidad de Los Andes (CECALCULA),
Corporación Parque Tecnológico de Mérida, Mérida 5101, Venezuela
e-mail: nunez@ula.ve
actualizado: Noviembre 2003
Movimiento Vertical: Trayectorias de Gotas, Balas, Corchos y Burbujas en Fluidos
Esta hoja de trabajo muestra la evolución de un gota, una bala y una burbuja lanzadas (o dejadas caer) verticalmente en presencia del resitencia del aire
o un fluido cualquiera.. El movimiento se describe mediante la ecuación diferencial y se modela el efecto de la resitencia del aire.
Para el modelaje tomamos:
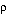 0 la densidad del fluido y
0 la densidad del fluido y 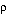 1 la densidad del cuerpo (gotas/balas/conchos/burbujas) en Kilogramos/
1 la densidad del cuerpo (gotas/balas/conchos/burbujas) en Kilogramos/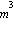
K es el coeficiente de fricción que depende de la forma de cuerpo. En el caso de una esfera en un fluido K=6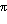 R y
R y
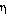 es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg /
es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg /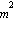 y se mide en Poise que es igual a un décimo de la unidad en MKS.
y se mide en Poise que es igual a un décimo de la unidad en MKS.
g es la aceleración de gravedad, la cual consideramos constante igual a 9.8 metros por segundo cuadrado
y(t) es la altura del movil (gotas, balas, corchos o burbujas) en un tiempo t.
La evolución en el tiempo viene gobernada por una ecuación diferencial de segundo orden.
| > |
m0:=(4*Pi/3)*rho0*R^3;
m:=(4*Pi/3)*rho1*R^3;
rho0:=xi*rho;
rho1:=phi*rho; |
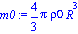
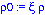
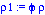
Donde 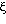 y
y 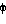 representan las densidades relativas del fluido y del cuerpo respecto al agua (de densidad
representan las densidades relativas del fluido y del cuerpo respecto al agua (de densidad 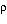 ), respectivamente.
), respectivamente.
Para el caso de una gota de lluvia cayendo, una pelota lanzada hacia arriba o una burbuja (o un corcho) que se despega desde el fondo
de un vaso de refresco, la ecuación diferencial que describe el moviento puede ser escrita como
| > |
emov := m*diff(y(t),t$2) = m*g - K*eta*diff(y(t),t)-m0*g ;
K:=6*Pi*R; |
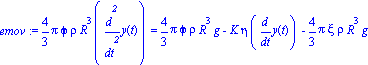
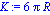
Tenemos tres fuerzas presentes: el peso, la resistencia del aire y la fuerza de Arquímides (empuje o flotación).
La solución general será:
| > |
soluciongeneral := dsolve( emov, y(t) ); |
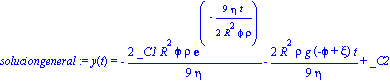
Donde _C1 y _C2 son constantes a ser determinadas por las condiciones iniciales. Es de hacer notar que, primeramente, una misma ecuación diferencial describe una variedad de fenómenos físicos. Igualmente, es importante señalar que la ecuación queda parametrizada 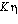 ,
,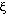 ,
,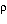 y
y 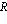 . Estas cantidades nos permiten modelar el fenómeno.
. Estas cantidades nos permiten modelar el fenómeno.
Para el caso de la gota de agua supondremos que parte del reposo, por lo tanto la solución general será:
| > |
solucionparticular := dsolve( {emov,y(0)=0,D(y)(0)=v0}, y(t) ); |
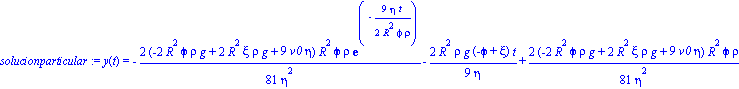
La posición y la velocidad vendrán dadas por
| > |
posicion:=rhs(solucionparticular); |
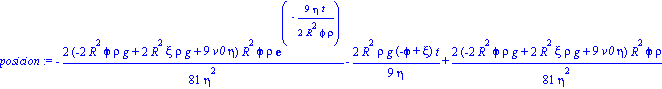
| > |
velocidad:=diff(posicion,t); |
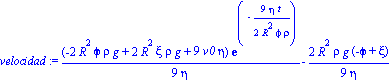
El cambio de signo en las fuerzas indica que en algún momento la fuerza de fricción y el empuje anularán al peso. En ese caso estaremos
hablando una velocidad límite. Es decir de una velocidad a partir de la cual el movil cae sin aceleración.
| > |
ecuac1:=0=rhs(emov):
vellimite:= simplify((4/3*Pi*(rho1-rho0)*R^3*g)/(6*Pi*R*eta)); |
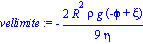
La velocidad límite será constante. En el caso de una gota de lluvia la densidad del aire respecto al agua es 1,30 10(-3), y consideremos el diámetro de la gota de agua 1mm= 10(-3)m.
| > |
gota:= [g = 9.8, R=0.001,rho=10^3, xi=1.3*10^(-3), phi=1, v0=0,eta=0.01894*10^(-3)]:
vellim:=subs(gota,vellimite); |
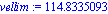
La gota tiene una velocidad límite de 120 mts/sg o
| > |
vellimiteKmh:=vellim*(0.001 / ( (1/60)*(1/60) )); |
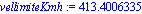
¡ casi 500 Kmh !
| > |
vel1:=subs(gota,velocidad);
plot(vel1,t=0..100,labels=[t,v]); |
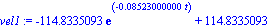
![[Plot]](simulacionesimag/Simulaciones_28.gif)
| > |
pos1:=subs(gota,posicion);
plot(pos1,t=0..100,labels=[t,y]); |
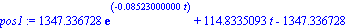
![[Plot]](simulacionesimag/Simulaciones_30.gif)
Si la gota crece a 0,2, 0,3, 0,4, 0,5 mm tendremos
| > |
gota2:= [g = 9.8, R=0.002,rho=10^3, xi=1.3*10^(-3), phi=1,v0=0,eta=1.81*10^(-5)]:
gota3:= [g = 9.8, R=0.003,rho=10^3, xi=1.3*10^(-3),phi=1, v0=0,eta=1.81*10^(-5)]:
gota4:= [g = 9.8, R=0.004,rho=10^3,phi=1, xi=1.3*10^(-3), v0=0,eta=1.81*10^(-5)]:
gota5:= [g = 9.8, R=0.005,rho=10^3, xi=1.3*10^(-3), phi=1,v0=0,eta=1.81*10^(-5)]: |
| > |
vel2:=subs(gota2,velocidad):
vel3:=subs(gota3,velocidad):
vel4:=subs(gota4,velocidad):
vel5:=subs(gota5,velocidad):
plot([vel1,vel2,vel3,vel4,vel5],t=0..300,labels=[t,v],color=[red,green,blue,yellow,black]); |
![[Plot]](simulacionesimag/Simulaciones_31.gif)
| > |
pos2:=subs(gota2,posicion):
pos3:=subs(gota3,posicion):
pos4:=subs(gota4,posicion):
pos5:=subs(gota5,posicion):
plot([pos1,pos2,pos3,pos4,pos5],t=0..300,labels=[t,y],color=[red,green,blue,yellow,black]); |
![[Plot]](simulacionesimag/Simulaciones_32.gif)
Consideremos el caso de una bala disparada verticalmente hacia arriba. Una bala la podemos aproximar por una esfera de 10 mm con 15 gr de masa y
se dispara con una velocidad de 600 m/sg. La densidad del hierro relativa al agua es 7,86
| > |
velocidadsr:=v0-g*t;
posicionsr:=v0*t-g*t^2/2; |

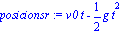
| > |
balasr:=[g=9.8,v0=600]:
velsr:=subs(balasr,velocidadsr);
possr:=subs(balasr,posicionsr); |

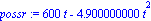
| > |
bala:= [g = -9.8, R=0.01,rho=10^3, xi=1.3*10^(-3), phi=7.86, v0=600,eta=1.81*10^(-5)]:
vel1:=subs(bala,velocidad); plot([vel1,velsr],t=0..125,labels=[t,v]); |
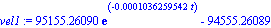
![[Plot]](simulacionesimag/Simulaciones_38.gif)
| > |
pos1:=subs(bala,posicion); plot([pos1,possr],t=0..125,labels=[t,y]); |
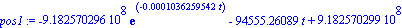
![[Plot]](simulacionesimag/Simulaciones_40.gif)
Si aumentamos la viscosidad del liquido a agua, aceite y glicerina
| > |
bala2:= [g = -9.8, R=0.01,rho=10^3, xi=1.3*10^(-3), phi=7.86, v0=600,eta=1.002*10^(-3)]:
bala3:= [g = -9.8, R=0.01,rho=10^3, xi=1.3*10^(-3), phi=7.86, v0=600,eta=130*10^(-3)]:
bala4:= [g = -9.8, R=0.01,rho=10^3, xi=1.3*10^(-3), phi=7.86, v0=600,eta=629*10^(-3)]: |
| > |
vel2:=subs(bala2,velocidad):
vel3:=subs(bala3,velocidad):
vel4:=subs(bala4,velocidad):
plot([vel1,vel2,vel3,vel4],t=0..60,labels=[t,v],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_41.gif)
| > |
pos2:=subs(bala2,posicion):
pos3:=subs(bala3,posicion):
pos4:=subs(bala4,posicion):
plot([pos1,pos2,pos3,pos4],t=0..60,labels=[t,y],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_42.gif)
recortanto la escala de tiempo a t= 6sg
| > |
plot([vel1,vel2,vel3,vel4],t=0..6,labels=[t,v],color=[red,green,blue,yellow]);
|
![[Plot]](simulacionesimag/Simulaciones_43.gif)
| > |
plot([pos1,pos2,pos3,pos4],t=0..6,labels=[t,y],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_44.gif)
y a t=0.6sg
| > |
plot([vel1,vel2,vel3,vel4],t=0..0.6,labels=[t,v],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_45.gif)
| > |
plot([pos1,pos2,pos3,pos4],t=0..0.6,labels=[t,y],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_46.gif)
y a t=0.06sg
| > |
plot([vel1,vel2,vel3,vel4],t=0..0.06,labels=[t,v],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_47.gif)
| > |
plot([pos1,pos2,pos3,pos4],t=0..0.06,labels=[t,y],color=[red,green,blue,yellow]); |
![[Plot]](simulacionesimag/Simulaciones_48.gif)
Consideremos ahora un corcho esferico que parte del reposo en el fondo de recipiente con agua, también tendrá una velocidad
límite dada por
| > |
corcho:= [g = -9.8, R=0.02,rho=10^3, xi=1, phi=0.8, v0=0,eta=1.002*10^(-3)]:
vellim:=subs(corcho,vellimite); |
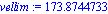
y podremos graficar su velocidad y su aceleración
| > |
vel1:=subs(corcho,velocidad);
plot(vel1,t=0..300,labels=[t,v]); |
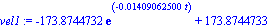
![[Plot]](simulacionesimag/Simulaciones_51.gif)
| > |
pos1:=subs(corcho,posicion);
plot(pos1,t=0..300,labels=[t,y]); |
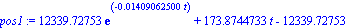
![[Plot]](simulacionesimag/Simulaciones_53.gif)
Al cambiar la viscosidad a aceite y reducir el tiempo
| > |
corcho2:= [g = -9.8, R=0.02,rho=10^3, xi=1, phi=0.8, v0=0,eta=130*10^(-3)]:
corcho3:= [g = -9.8, R=0.02,rho=10^3, xi=1, phi=0.8, v0=0,eta=629*10^(-3)]: |
| > |
vel2:=subs(corcho2,velocidad):
vel3:=subs(corcho3,velocidad):
plot([vel1,vel2,vel3],t=0..20,labels=[t,v],color=[red,green,blue]); |
![[Plot]](simulacionesimag/Simulaciones_54.gif)
| > |
pos2:=subs(corcho2,posicion):
pos3:=subs(corcho3,posicion):
plot([pos1,pos2,pos3],t=0..20,labels=[t,y],color=[red,green,blue]); |
![[Plot]](simulacionesimag/Simulaciones_55.gif)
Finalmente supongamos una burbuja. Por lo tanto, el radio de la burbuja varia con la presión. Si suponemos que la burbuja
está compuesta por un gas ideal tendremos que
P V = NRT = cte = P0 V0
donde P0 y V0 son la presión y el volumen inicial respectivamente.
Ahora bien, si la presión en un líquido viene dada por P = rho g y(t), con y(t) la profundidad, tendremos que
rho * g * y(t) * (4/3)* Pi * R(t)^3= (P0 * V0)= rho * g * y(0) * (4/3) * Pi * R(0)^3
con lo cual
| > |
restart:R:=gamma0*y(t)^(-1/3); |
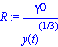
donde gamma =R(0) * ( y(0))^(1/3)
nótese que la masa de la burbuja es constante, no así la masa desplazada por ella. Adicionalmente que hemos
cambiado el origen de coordenadas y ahora la posición inicial, y(0) = y0 es distinta de cero.
| > |
gamma0 := R0*y0^(1/3);
m0:=(4*Pi/3)*rho0*R^3;
mB:=(4*Pi/3)*rho1*R0^3;
rho0:=xi*rho;
rho1:=phi*rho;
K:=6*Pi*R; |
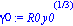

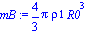
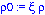
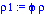
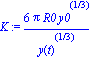
Donde 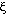 y
y 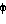 representan las densidad relativas del fluido y del cuerpo respecto al agua (de densidad
representan las densidad relativas del fluido y del cuerpo respecto al agua (de densidad  ), respectivamente. Por su parte
), respectivamente. Por su parte
R0 representa el radio inicial de la burbuja.
Para el caso una burbuja que se despega desde el fondo de un vaso de refresco la ecuación diferencial que describe el moviento
puede ser escrita como
| > |
emov2 := mB*diff(y(t),t$2) = -mB*g - K*eta*diff(y(t),t)+m0*g ; |
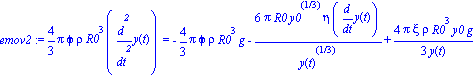
| > |
dsolve({emov2,y(0)=-y0,D(y)(0)=0},y(t)); |
Por lo tanto debemos resolverla numéricamente. Para ello es imperioso adimensionalizarla. La integración numérica se hace
sobre números, por lo que las variables deben ser adimensionales. Para ello cambiamos la variable independiente (el tiempo, t)
y la variable dependiente (la profundidad, y(t)) por
tt = t/tfinal y yy(tt) = y(t)/y(0)
| > |
emov2AD := mB*diff(yy(tt),tt$2)(y0/(tfinal^2)) = -mB*g -6*Pi*R0/yy(tt)^(1/3)*eta*diff(yy(tt),tt)*(y0/tfinal)+4/3*Pi*xi*rho*R0^3/yy(tt)*g; |
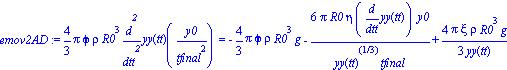
acomodando un poco queda como
| > |
emov2AD1:=diff(yy(tt),tt$2)=-(g/(y0/tfinal^2))
-(6*Pi*R0/yy(tt)^(1/3)*eta*diff(yy(tt),tt)*y0/tfinal)/(4/3*Pi*phi*rho*R0^3*(y0/tfinal^2))
+(4/3*Pi*xi*rho*R0^3/yy(tt)*g)/(4/3*Pi*phi*rho*R0^3*(y0/tfinal^2)); |
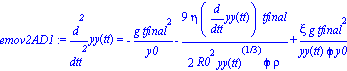
y ahora convertimos esta ecuación de segundo orden en, dos ecuaciones de primer orden mediante un cambio de
variable
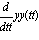 = pp(tt) con lo cual
= pp(tt) con lo cual 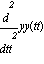 =
= 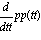
y entonces el sistema queda como
| > |
ecuac1a:=diff(yy(tt),tt)=pp(tt);
ecuac1b:=diff(pp(tt),tt) = -g/y0*tfinal^2 -9/2*1/R0^2/yy(tt)^(1/3)*eta*pp(tt)*tfinal/phi/rho +xi/yy(tt)*g/phi/y0*tfinal^2; |
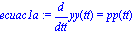
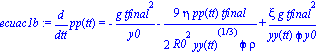
para una burbuja e agua esto es: 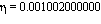
| > |
burbuja110:= [g = -9.8, R0=0.002,rho=10^3, xi=1, phi=0.08, eta=1.002*10^(-3),y0 =-10, tfinal=50]:
ecuac1a1:=subs(burbuja110,ecuac1a);
ecuac1b1:=subs(burbuja110,ecuac1b);
sist1:=ecuac1a1,ecuac1b1:
|
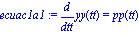
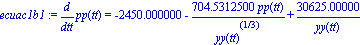
| > |
with(plots):Digits:=20:
sol:=dsolve({sist1,pp(0)=0,yy(0)=1},{pp(tt),yy(tt)},numeric,stiff=true,range=0..1);
odeplot(sol,[tt,yy(tt)],0..1,numpoints=500,title="posicion vs tiempo"); |
Warning, the name changecoords has been redefined

![[Plot]](simulacionesimag/Simulaciones_78.gif)
y lha gráfica de la velocidad será
| > |
odeplot(sol,[tt,pp(tt)],0..1,numpoints=500,title="velocidad vs tiempo"); |
![[Plot]](simulacionesimag/Simulaciones_79.gif)
Equivalentemente, MAPLE puede resolver la ecuación de segundo orden directamente.
| > |
emov2AD10:= subs(burbuja110,emov2AD1);
sol2:=dsolve({emov2AD10,yy(0)=1,D(yy)(0)=0},numeric,stiff=true);
odeplot(sol2,[tt,yy(tt)],0..1,numpoints=50); |
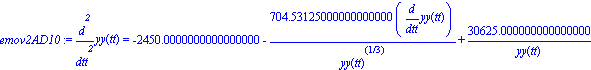
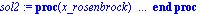
![[Plot]](simulacionesimag/Simulaciones_82.gif)
Movimiento Parabólico: Trayectoria de Balas en Fluidos
Warning, the name changecoords has been redefined
Toca ahora simular el lanzamiento de proyectiles en Fluidos. En física general, aún en secundaria, es proverbial resolver el movimiento en dos dimensiones (2D) con atracción gravitatoria. En esas tempranas épocas de nuestro conocimiento de física a este ``problema'' se le conoce con
el nombre de movimiento parabólico, por la trayectoria que describe el objeto.
Si suponemos un cuerpo de masa constante, m, que se mueve en un fluido con resitencia de despreciable las ecuaciones diferenciales que
describen el movimiento no pueden ser otras que aquellas que provengan de las ecuaciones de Newton y en este caso corresponden a
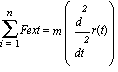
donde r(t) es el radio vector posicion.
| > |
ecuac1xlib:=m*diff(xlib(t),t,t)=0;
ecuac1ylib:=m*diff(ylib(t),t,t)=-m*g; |
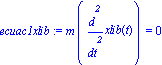
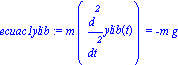
las cuales se resuelven de forma inmediata
| > |
solxlib:=dsolve({ecuac1xlib,xlib(0)=x0,D(xlib)(0)=V0x});
solylib:=dsolve({ecuac1ylib,ylib(0)=y0,D(ylib)(0)=V0y});
assign(solxlib):assign(solylib): |

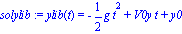
que no son otra cosa que las formulitas que siempre nos aprendimos
| > |
otrosparamlib:=[g=9.8]:
pos0:=[x0=0,y0=0]:
vel0pi12:=[V0x=600*evalf(cos(Pi/12)),V0y=600*evalf(sin(Pi/12))]:
vel0pi6:=[V0x=600*evalf(cos(Pi/6)),V0y=600*evalf(sin(Pi/6))]:
vel0pi4:=[V0x=600*evalf(cos(Pi/4)),V0y=600*evalf(sin(Pi/4))]:
vel0pi3:=[V0x=600*evalf(cos(Pi/3)),V0y=600*evalf(sin(Pi/3))]:
vel05pi12:=[V0x=600*evalf(cos(5*Pi/12)),V0y=600*evalf(sin(5*Pi/12))]: |
| > |
xpi12(t):=subs(pos0,vel0pi12,otrosparamlib,xlib(t)):
ypi12(t):=subs(pos0,vel0pi12,otrosparamlib,ylib(t)):
grafpi12:=plot([xpi12(t),ypi12(t),t=0..500],scaling=constrained):
xpi6(t):=subs(pos0,vel0pi6,otrosparamlib,xlib(t)):
ypi6(t):=subs(pos0,vel0pi6,otrosparamlib,ylib(t)):
grafpi6:=plot([xpi6(t),ypi6(t),t=0..500],scaling=constrained):
xpi4(t):=subs(pos0,vel0pi4,otrosparamlib,xlib(t)):
ypi4(t):=subs(pos0,vel0pi4,otrosparamlib,ylib(t)):
grafpi4:=plot([xpi4(t),ypi4(t),t=0..500],scaling=constrained):
xpi3(t):=subs(pos0,vel0pi3,otrosparamlib,xlib(t)):
ypi3(t):=subs(pos0,vel0pi3,otrosparamlib,ylib(t)):
grafpi3:=plot([xpi3(t),ypi3(t),t=0..500],scaling=constrained):
x5pi12(t):=subs(pos0,vel05pi12,otrosparamlib,xlib(t)):
y5pi12(t):=subs(pos0,vel05pi12,otrosparamlib,ylib(t)):
graf5pi12:=plot([x5pi12(t),y5pi12(t),t=0..500],scaling=constrained):
display({grafpi12,grafpi6,grafpi4,grafpi3,graf5pi12},view=[0..40000,0..20000],
title="Movimiento Parabólico, sin roce",labels=["x(t)","y(t)"]); |
![[Plot]](simulacionesimag/Simulaciones_88.gif)
arriba se ilustra las trayectorias correspondientes a distintos movimientos parabólicos con una velocidad inicial ![V[0] = 25](simulacionesimag/Simulaciones_89.gif) y distintos águlos de
y distintos águlos de
disparo 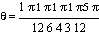
Una cosa distinta se presenta para el movimiento en 2D con resistencia del aire. En este caso, como en todos los casos en los cuales una
fuerza de origen microscópico es descrita macroscópicamente, su representación matemática es fenomenológica. Vale decir, mediante una
fórmula matemática, utilizamos una descripción promedio de su efecto. En el caso de la fuerza de roce en fluidos se presentan dos casos:
uno en el cual la fuerza de resistencia con el aire es proporcional a la velocidad, ![f[roce] = -K*eta*sqrt(V[x]^2+V[y]^2)*U[v]](simulacionesimag/Simulaciones_91.gif) y otro en el cual supondremos la fuerza de roce proporcional al cuadrado de su velocidad,
y otro en el cual supondremos la fuerza de roce proporcional al cuadrado de su velocidad, ![f[roce] = -K*eta*(V[x]^2+V[y]^2)*U[v]](simulacionesimag/Simulaciones_92.gif) En estos casos
En estos casos ![U[v]](simulacionesimag/Simulaciones_93.gif) es el vector unitario en la dirección
es el vector unitario en la dirección
tangente ![U[v] = V[x]*i/(V[x]^2+V[y]^2)^(1/2)+V[y]*j/(V[x]^2+V[y]^2)^(1/2)](simulacionesimag/Simulaciones_94.gif) y
y 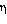 es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg /
es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg / y se mide en Poise que es igual a un décimo de la unidad en MKS. Esto es 10P=1×N sg/m2 En ambos casos K es el coeficiente de fricción que depende de la forma de cuerpo. Para una esfera de Radio, R, tendremos K=6
y se mide en Poise que es igual a un décimo de la unidad en MKS. Esto es 10P=1×N sg/m2 En ambos casos K es el coeficiente de fricción que depende de la forma de cuerpo. Para una esfera de Radio, R, tendremos K=6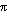 R. La utilización de una u otra expresión para la fuerza de roce se basa en la magnitud de la velocidad del cuerpo respecto al fluido. Para los casos en los cuales la velocidad del cuerpo es mucho menor a la velocidad del sonido, la fuerza de roce será proporcional a la velocidad. En aquellos casos en los cuales el orden de magnitud del módulo de la velocidad del cuerpo sea el de la velocidad del sonido en ese medio, utilizaremos que la fuerza de roce será proporcional al cuadrado de la velocidad.
R. La utilización de una u otra expresión para la fuerza de roce se basa en la magnitud de la velocidad del cuerpo respecto al fluido. Para los casos en los cuales la velocidad del cuerpo es mucho menor a la velocidad del sonido, la fuerza de roce será proporcional a la velocidad. En aquellos casos en los cuales el orden de magnitud del módulo de la velocidad del cuerpo sea el de la velocidad del sonido en ese medio, utilizaremos que la fuerza de roce será proporcional al cuadrado de la velocidad.
Con lo cual para el caso de desplazamientos lentos a través de fluidos tendremos
| > |
ecuacxrocelent:=m*diff(xrocelent(t),t,t)=
-K*eta*sqrt(diff(xrocelent(t),t)^2 +diff(yrocelent(t),t)^2 )*(diff(xrocelent(t),t)/
(sqrt(diff(xrocelent(t),t)^2 +diff(yrocelent(t),t)^2 )));
ecuacyrocelent:=m*diff(yrocelent(t),t,t)=-m*g
-K*eta*sqrt(diff(xrocelent(t),t)^2 +diff(yrocelent(t),t)^2 )*(diff(yrocelent(t),t)/
(sqrt(diff(xrocelent(t),t)^2 +diff(yrocelent(t),t)^2 )));
|

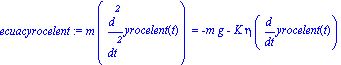
Las cuales pueden ser integradas analíticamente como
| > |
K:=6*Pi*R;
solxrocelent:=dsolve({ecuacxrocelent,xrocelent(0)=x0,D(xrocelent)(0)=V0x});
solyrocelent:=dsolve({ecuacyrocelent,yrocelent(0)=y0,D(yrocelent)(0)=V0y});
assign(solxrocelent);
assign(solyrocelent); |
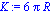
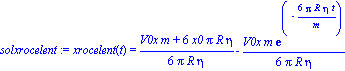
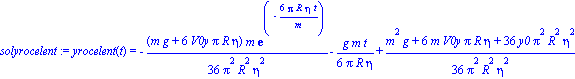
Ahora sustituimos los valores para distintas fuerzas de roce: aire, agua y aceite
| > |
otrosparamroceaire:=[g=9.8,m=0.015,eta=0.01894*10^(-3),R=0.015]:
xpi12lent(t):=subs(pos0,vel0pi12,otrosparamroceaire,xrocelent(t)):
ypi12lent(t):=subs(pos0,vel0pi12,otrosparamroceaire,yrocelent(t)):
grafpi12lentaire:=plot([xpi12lent(t),ypi12lent(t),t=0..500],scaling=constrained):
xpi6lent(t):=subs(pos0,vel0pi6,otrosparamroceaire,xrocelent(t)):
ypi6lent(t):=subs(pos0,vel0pi6,otrosparamroceaire,yrocelent(t)):
grafpi6lentaire:=plot([xpi6lent(t),ypi6lent(t),t=0..500],scaling=constrained):
xpi4lent(t):=subs(pos0,vel0pi4,otrosparamroceaire,xrocelent(t)):
ypi4lent(t):=subs(pos0,vel0pi4,otrosparamroceaire,yrocelent(t)):
grafpi4lentaire:=plot([xpi4lent(t),ypi4lent(t),t=0..500],scaling=constrained):
xpi3lent(t):=subs(pos0,vel0pi3,otrosparamroceaire,xrocelent(t)):
ypi3lent(t):=subs(pos0,vel0pi3,otrosparamroceaire,yrocelent(t)):
grafpi3lentaire:=plot([xpi3lent(t),ypi3lent(t),t=0..500],scaling=constrained):
x5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceaire,xrocelent(t)):
y5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceaire,yrocelent(t)):
graf5pi12lentaire:=plot([x5pi12lent(t),y5pi12lent(t),t=0..500],scaling=constrained): |
| > |
otrosparamroceagua:=[g=9.8,m=0.015,eta=1.002*10^(-3),R=0.015]:
xpi12lent(t):=subs(pos0,vel0pi12,otrosparamroceagua,xrocelent(t)):
ypi12lent(t):=subs(pos0,vel0pi12,otrosparamroceagua,yrocelent(t)):
grafpi12lentagua:=plot([xpi12lent(t),ypi12lent(t),t=0..500],scaling=constrained):
xpi6lent(t):=subs(pos0,vel0pi6,otrosparamroceagua,xrocelent(t)):
ypi6lent(t):=subs(pos0,vel0pi6,otrosparamroceagua,yrocelent(t)):
grafpi6lentagua:=plot([xpi6lent(t),ypi6lent(t),t=0..500],scaling=constrained):
xpi4lent(t):=subs(pos0,vel0pi4,otrosparamroceagua,xrocelent(t)):
ypi4lent(t):=subs(pos0,vel0pi4,otrosparamroceagua,yrocelent(t)):
grafpi4lentagua:=plot([xpi4lent(t),ypi4lent(t),t=0..500],scaling=constrained):
xpi3lent(t):=subs(pos0,vel0pi3,otrosparamroceagua,xrocelent(t)):
ypi3lent(t):=subs(pos0,vel0pi3,otrosparamroceagua,yrocelent(t)):
grafpi3lentagua:=plot([xpi3lent(t),ypi3lent(t),t=0..500],scaling=constrained):
x5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceagua,xrocelent(t)):
y5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceagua,yrocelent(t)):
graf5pi12lentagua:=plot([x5pi12lent(t),y5pi12lent(t),t=0..500],scaling=constrained): |
| > |
otrosparamroceaceite:=[g=9.8,m=0.015,eta=130*10^(-3),R=0.015]:
xpi12lent(t):=subs(pos0,vel0pi12,otrosparamroceaceite,xrocelent(t)):
ypi12lent(t):=subs(pos0,vel0pi12,otrosparamroceaceite,yrocelent(t)):
grafpi12lentaceite:=plot([xpi12lent(t),ypi12lent(t),t=0..500],scaling=constrained):
xpi6lent(t):=subs(pos0,vel0pi6,otrosparamroceaceite,xrocelent(t)):
ypi6lent(t):=subs(pos0,vel0pi6,otrosparamroceaceite,yrocelent(t)):
grafpi6lentaceite:=plot([xpi6lent(t),ypi6lent(t),t=0..500],scaling=constrained):
xpi4lent(t):=subs(pos0,vel0pi4,otrosparamroceaceite,xrocelent(t)):
ypi4lent(t):=subs(pos0,vel0pi4,otrosparamroceaceite,yrocelent(t)):
grafpi4lentaceite:=plot([xpi4lent(t),ypi4lent(t),t=0..500],scaling=constrained):
xpi3lent(t):=subs(pos0,vel0pi3,otrosparamroceaceite,xrocelent(t)):
ypi3lent(t):=subs(pos0,vel0pi3,otrosparamroceaceite,yrocelent(t)):
grafpi3lentaceite:=plot([xpi3lent(t),ypi3lent(t),t=0..500],scaling=constrained):
x5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceaceite,xrocelent(t)):
y5pi12lent(t):=subs(pos0,vel05pi12,otrosparamroceaceite,yrocelent(t)):
graf5pi12lentaceite:=plot([x5pi12lent(t),y5pi12lent(t),t=0..500],scaling=constrained): |
| > |
display({grafpi12,grafpi6,grafpi4,grafpi3,graf5pi12},view=[0..40000,0..20000],
title="Movimiento Parabólico, sin roce",labels=["x(t)","y(t)"]);
display({grafpi12lentaire,grafpi6lentaire,grafpi4lentaire,grafpi3lentaire,graf5pi12lentaire },view=[0..40000,0..20000],
title="Movimiento Parabólico lento, con roce en aire",labels=["x(t)","y(t)"]);
display({grafpi12lentagua,grafpi6lentagua,grafpi4lentagua,grafpi3lentagua,graf5pi12lentagua},view=[0..20000,0..12000],
title="Movimiento Parabólico lento, con roce en agua",labels=["x(t)","y(t)"]);
display({grafpi12lentaceite,grafpi6lentaceite,grafpi4lentaceite,grafpi3lentaceite,graf5pi12lentaceite},view=[0..500,0..250],
title="Movimiento Parabólico lento, con roce en aceite",labels=["x(t)","y(t)"]); |
![[Plot]](simulacionesimag/Simulaciones_103.gif)
![[Plot]](simulacionesimag/Simulaciones_104.gif)
![[Plot]](simulacionesimag/Simulaciones_105.gif)
![[Plot]](simulacionesimag/Simulaciones_106.gif)
También podemos graficar disparos con un mismo ángulo y distintos medios dispersivos
| > |
display({grafpi6,grafpi6lentaire,grafpi6lentagua,grafpi6lentaceite},view=[0..32000,0..5000],
title="Movimiento Parabólico, para un ángulo Pi/6",labels=["x(t)","y(t)"]); |
![[Plot]](simulacionesimag/Simulaciones_107.gif)
Supongamos que ahora la fuerza de roce es proporcional al cuadrado de la velocidad. Esto implica que las ecuaciones quedan como
| > |
ecuacxrocerap:=m*diff(xrocerap(t),t,t)=
-K*eta*(diff(xrocerap(t),t)^2 +diff(yrocerap(t),t)^2 )*(diff(xrocerap(t),t)/
(sqrt(diff(xrocerap(t),t)^2 +diff(yrocerap(t),t)^2 )));
ecuacyrocerap:=m*diff(yrocerap(t),t,t)=-m*g
-K*eta*(diff(xrocerap(t),t)^2 +diff(yrocerap(t),t)^2 )*(diff(yrocerap(t),t)/
(sqrt(diff(xrocerap(t),t)^2 +diff(yrocerap(t),t)^2 )));
|
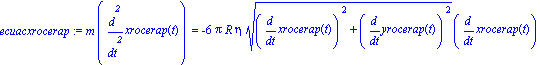
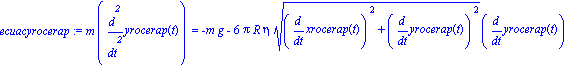
que ahora están mexcladas y el sistema de ecuaciones diferenciales NO se separa.
El Péndulo Físico
Oscilador Armónico Simple
Alguien, de los famosos de Física, dijo una vez: quien entienda el oscilador armónico simple en todas sus facetas, entiende la mitad de toda la Física. Por ello vamos a tratar de estudiarlo. Llamaremos Oscilador armónico simple o pendulo físico linealizado aquel sistema físico que tiene oscilaciones pequeñas y por lo tanto se puede linealizar la ecuación diferencial
Oscilador Armónico Simple Libre y no amorgiguado)
El oscilador armónico simple, libre tiene como ecuación diferecial
| > |
ecuacosarmsimple:=diff(xsimp(t),t$2)=-(omega0^2)*xsimp(t); |
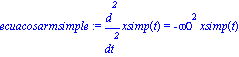
que tendrá como solución
| > |
solxsimpt:=dsolve({ecuacosarmsimple,xsimp(0)=x0,D(xsimp)(0)=v0},xsimp(t));
assign(solxsimpt);vsimp(t):=diff(xsimp(t),t); |
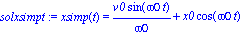

Supongamos que 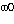 = 2 y que el movil parte de x0 = 0 con distintas velocidades iniciales. Vale decir
= 2 y que el movil parte de x0 = 0 con distintas velocidades iniciales. Vale decir
v(0) = 3, 5, 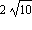 , 7, 8.
, 7, 8.
| > |
omega0:='omega0';x0:='x0'; v0:='v0';
Xsimp:=unapply(xsimp(t),omega0,x0,v0,t);
Vsimp:=unapply(vsimp(t),omega0,x0,v0,t); |
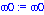
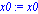
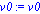
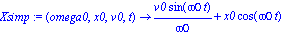
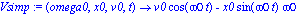
con lo cual obtendremos la siguiente gráfica posición tiempo
| > |
plot([Xsimp(2,0,3,t),Xsimp(2,0,5,t),Xsimp(2,0,2*sqrt(10),t),Xsimp(2,0,7,t),Xsimp(2,0,8,t)],t=0..4*Pi,labels=[t,"xsimp"], title="Oscilador Armonico Simple, Evolucion temporal",scaling=constrained); |
![[Plot]](simulacionesimag/Simulaciones_120.gif)
y la representación en el espacio de fases será
| > |
plot({[Xsimp(2,0,3,t),Vsimp(2,0,3,t),t=0..2*Pi],
[Xsimp(2,0,5,t),Vsimp(2,0,5,t),t=0..2*Pi],
[Xsimp(2,0,2*sqrt(10),t),Vsimp(2,0,2*sqrt(10),t),t=0..2*Pi],
[Xsimp(2,0,7,t),Vsimp(2,0,7,t),t=0..2*Pi],
[Xsimp(2,0,8,t),Vsimp(2,0,8,t),t=0..2*Pi] },
scaling=constrained,labels=[xsimp,vsimp],title="Oscilador Armonico Simple, Diagrama de Fase "); |
![[Plot]](simulacionesimag/Simulaciones_121.gif)
En muchos problemas esta primera integral será fácil de obtener, no así la integral de la posición respecto al tiempo. Por ello
son muy útiles las gráficas V(t) vs X(t). Esas gráficas se denominan gáficas del espacio de fases, y cada
una de ellas representa un valor distinto para la energia. En ella los puntos de equilibrio se idenfican gráficamente. En este caso el
punto de equilibrio, como se esperaba, es
Esto se obtiene fácilmente si multiplicamos por V(t) = 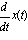 e integrando.
e integrando.
| > |
ecuacE:= E=(1/2)*omega^2 + (1/2)*omega0^2*theta^2; |

primer término representa la energía cinética y el segundo la energía potencial gravitatoria. Cada una de las elipses le corresponde un valor de la Energía total
Oscilador Armónico Amortiguado
Si consideramos el caso del oscilador armonico amortiguado, tendremos que la ecuación diferencial será
| > |
ecuacosarmamort:=diff(xamort(t),t$2)=-2*mu*diff(xamort(t),t)-(omega0^2)*xamort(t); |
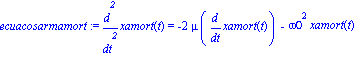
y su solución será
| > |
solxamortt:=dsolve({ecuacosarmamort,xamort(0)=x0,D(xamort)(0)=v0},xamort(t));
assign(solxamortt);vamort(t):=(diff(xamort(t),t)); |
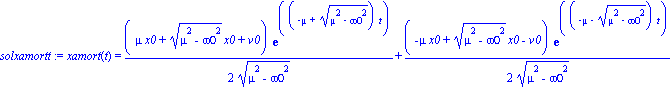
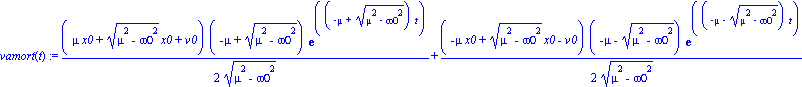
con lo cual tendremos tres soluciones dependiendo del valor (mayor, igual o menor que cero) de la cantidad subradical 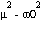 con lo cual tendremos los casos:
con lo cual tendremos los casos:
subamortiguado si 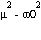 < 0;
< 0;
sobreamortiguado si 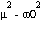 > 0 y
> 0 y
críticamente amortiguado si 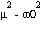 =0 .
=0 .
Estudiaremos los tres casos haciendo 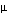 = 0,5, 3,5, y 2 respectivamente.
= 0,5, 3,5, y 2 respectivamente.
| > |
mu:='mu':
Xamort:=unapply(xamort(t),mu,omega0,x0,v0,t):
Vamort:=unapply(vamort(t),mu,omega0,x0,v0,t): |
Para el caso subamortiguado ( 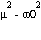 < 0; ) tendremos la evolución del sistema, dada por
< 0; ) tendremos la evolución del sistema, dada por
| > |
plot([Xamort(0.5,2,0,3,t),Xamort(0.5,2,0,5,t),Xamort(0.5,2,0,2*sqrt(10),t),Xamort(0.5,2,0,7,t),Xamort(0.5,2,0,8,t)],
t=0..4*Pi,labels=[t,"xamort"], title="Oscilador Armonico Amortiguado, Evolucion temporal",scaling=constrained,
view=[0..7,-1.5..3] ); |
![[Plot]](simulacionesimag/Simulaciones_133.gif)
y la representación en el espacio de fases será
| > |
plot({[Xamort(0.5,2,0,3,t),Vamort(0.5,2,0,3,t),t=0..2*Pi],[Xamort(0.5,2,0,5,t),Vamort(0.5,2,0,5,t),t=0..2*Pi],[Xamort(0.5,2,0,2*sqrt(10),t),Vamort(0.5,2,0,2*sqrt(10),t),t=0..2*Pi],[Xamort(0.5,2,0,7,t),Vamort(0.5,2,0,7,t),t=0..2*Pi],[Xamort(0.5,2,0,8,t),Vamort(0.5,2,0,8,t),t=0..2*Pi] }, scaling=constrained,labels=[xamort,vamort],title="Oscilador Armonico Subamortiguado, Diagrama de Fase "); |
![[Plot]](simulacionesimag/Simulaciones_134.gif)
Para el caso sobreamortiguado (si 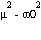 > 0 ) la evolución temporal del oscilador será
> 0 ) la evolución temporal del oscilador será
| > |
plot([Xamort(2.1,2,0,3,t),Xamort(2.1,2,0,5,t),Xamort(2.1,2,0,2*sqrt(10),t),Xamort(2.1,2,0,7,t),Xamort(2.1,2,0,8,t)],
t=0..4*Pi,labels=[t,"xamort"], title="Oscilador Armonico Sobreamortiguado, Evolucion temporal",scaling=constrained,
view=[0..5,0..1.5] ); |
![[Plot]](simulacionesimag/Simulaciones_136.gif)
mientras que el diagrama de fase será
| > |
plot({[Xamort(2.1,2,0,3,t),Vamort(2.1,2,0,3,t),t=0..2*Pi],[Xamort(2.1,2,0,5,t),Vamort(2.1,2,0,5,t),t=0..2*Pi],[Xamort(2.1,2,0,2*sqrt(10),t),Vamort(2.1,2,0,2*sqrt(10),t),t=0..2*Pi],[Xamort(2.1,2,0,7,t),Vamort(2.1,2,0,7,t),t=0..2*Pi],[Xamort(2.1,2,0,8,t),Vamort(2.1,2,0,8,t),t=0..2*Pi] }, scaling=constrained,labels=[xamort,vamort],title="Oscilador Armonico Sobreamortiguado, Diagrama de Fase "); |
![[Plot]](simulacionesimag/Simulaciones_137.gif)
El Péndulo Físico
Warning, the name changecoords has been redefined
Análisis del Movimiento
Consideremos ahora el caso sin aproximación, vale decir que la ecuación diferencial que describe la oscilación queda como
| > |
ecuacosarmtot:=diff(theta(t),t$2)=-(omega0^2)*sin(theta(t)); |
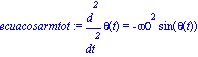
Que constituye el sistema físico: Péndulo Físico, libre y sin amortiguamiento. Es decir, el sistema equivalente, sin aproximación de ángulo pequeño, al del oscilador armónico simple.
La ecuación anterior tendrá como soluciones:
| > |
dsolve(ecuacosarmtot);assign(solthetat); |
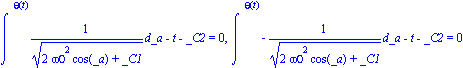
las cuales corresponden a integrales elípticas de primera especie, las cuales son forzozamente resueltas numéricamente.
Más aún, si procedemos a incorporar las condiciones iniciales, esto es, dejamos caer el cuerpo ( ![omega[0] = 0](simulacionesimag/Simulaciones_140.gif) ) el péndulo desde un ángulo
) el péndulo desde un ángulo ![theta(0) = theta[0]](simulacionesimag/Simulaciones_141.gif) tendremos las siguientes expresiones para la posición y la velocidad
tendremos las siguientes expresiones para la posición y la velocidad
| > |
solthetat:=dsolve({ecuacosarmtot,theta(0)=theta0,D(theta)(0)=dtheta0},theta(t));
assign(solthetat);omega(t):=(diff(theta(t),t)); |
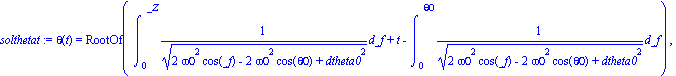

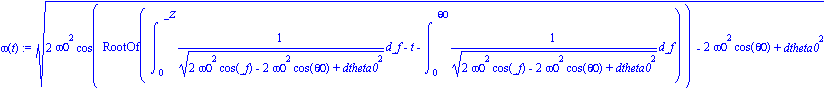
Necesariamente debemos proceder por otros métodos, en este caso analizar soluciones mediante g[raficos. La energía total del sistema vendrá dada por
| > |
ecuacpendulofisico:=C=Thetapunt^2/2 -omega0^2*cos(Theta); |
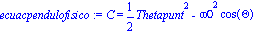
Procedemos a graficar el diagrama de fase para el péndulo físico libre para distintos valores de C
| > |
ecuacpendfisico9:=solve(subs([C=3.5,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico8:=solve(subs([C=3.9,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico7:=solve(subs([C=30,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico6:=solve(subs([C=20,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico5:=solve(subs([C=10,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico4:=solve(subs([C=8,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico3:=solve(subs([C=6,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico2:=solve(subs([C=4.1,omega0=2],ecuacpendulofisico),Thetapunt):
ecuacpendfisico1:=solve(subs([C=4.01,omega0=2],ecuacpendulofisico),Thetapunt):
plot({ecuacpendfisico1[1],ecuacpendfisico1[2],ecuacpendfisico2[1],ecuacpendfisico2[2],
ecuacpendfisico3[1],ecuacpendfisico3[2],ecuacpendfisico4[1],ecuacpendfisico4[2],
ecuacpendfisico5[1],ecuacpendfisico5[2],ecuacpendfisico6[1],ecuacpendfisico6[2],
ecuacpendfisico7[1],ecuacpendfisico7[2],ecuacpendfisico8[1],ecuacpendfisico8[2],
ecuacpendfisico9[1],ecuacpendfisico9[2]
},Theta=-3*Pi..3*Pi,scaling=constrained,labels=[theta,diftheta],title="Péndulo Físico, Diagrama de Fase "); |
![[Plot]](simulacionesimag/Simulaciones_146.gif)
Las curvas cerradas respresentan trayectorias oscilatorias mientras que para las abiertas el ángulo de giro crece contínuamente
El Período del Péndulo F[sico
Analicemos como varía el período de las soluciones oscilatorias. Para ello recordamos que el período del oscilador armónico simple viene dado por
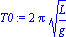
Mientra que el período para el Péndulo Físico viene de la Integración de la ecuación de la energía y es
| > |
4*sqrt(L/g)*Int(1/sqrt(1-sin(Phi/2)^2*sin(chi)^2 ), chi=0..Pi/2)=4*sqrt(L/g)*int(1/sqrt(1-sin(Phi/2)^2*sin(chi)^2 ), chi=0..Pi/2);
T:=4*sqrt(L/g)*int(1/sqrt(1-sin(Phi/2)^2*sin(chi)^2 ), chi=0..Pi/2): |
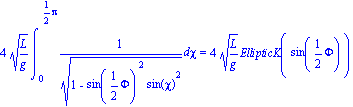
Es interesante que esa integral elíptica completa de primera especie puede ser aproximada por una serie, cuando el denominador del lado izquierdo se expande en términos del ángulo inicial de lanzamiento y se integra término a término.. Esto es:
| > |
T_T0=simplify(series(T/T0,Phi,5)); |
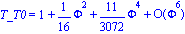
Con este expansión en series o directamente comparando la evaluación de la integral elíptica con el valor del período para el caso del oscilador armónico simple tendremos que podremos comprobar cuan buena es la aproximación que linealiza la función seno en la ecuación diferencial
Así, tendremos el siguiente cuadro de aproximación
| > |
T00:=evalf(subs([L=2,g=9.8],T0)):
TPi12:=evalf(subs([Phi=Pi/12,L=2,g=9.8],T )):Delta12:=100*(TPi12-T00)/TPi12:
TPi6:=evalf(subs([Phi=Pi/6,L=2,g=9.8],T )): Delta6:=100*(TPi6-T00)/TPi6:
TPi4:=evalf(subs([Phi=Pi/4,L=2,g=9.8],T )):Delta4:=100*(TPi4-T00)/TPi4:
TPi3:=evalf(subs([Phi=Pi/3,L=2,g=9.8],T )):Delta3:=100*(TPi3-T00)/TPi3:
TPi2:=evalf(subs([Phi=Pi/2,L=2,g=9.8],T )):Delta2:=100*(TPi2-T00)/TPi2:
T2Pi3:=evalf(subs([Phi=2*Pi/3,L=2,g=9.8],T )):Delta23:=100*(T2Pi3-T00)/T2Pi3:
array(1..3,1..7,[
[T00, pi/12, pi/6, pi/4, pi/3,pi/2,2*pi/3],
["Periodo",TPi12,TPi6,TPi4,TPi3,TPi2,T2Pi3],
["Error",Delta12,Delta6,Delta4,Delta3,Delta2,Delta23] ]); |
![matrix([[2.838453791, 1/12*pi, 1/6*pi, 1/4*pi, 1/3*pi, 1/2*pi, 2/3*pi], [](simulacionesimag/Simulaciones_150.gif)
Es claro que la aproximación es buena, ya que hasta ángulos cercanos a 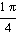 el error que se obtiene es del orden del 3%
el error que se obtiene es del orden del 3%
Integración Numérica de la Ecuación de Movimiento
Proderemos a integrar numéricamente la ecuación diferencial del péndulo físico, en este caso para un ángulo inicial de lanzamiento ![theta[0] = 0](simulacionesimag/Simulaciones_152.gif) y para distintos valores de la velocidad inicial
y para distintos valores de la velocidad inicial
A partir de las ecuacion
| > |
restart;with(plots);diff(theta(t),t$2)=-(omega0^2)*sin(theta(t)); |
Warning, the name changecoords has been redefined




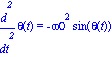
Que es una ecuación diferencial, no lineal de segundo orden, construimos varios sistemas ADIMENSIONALES de ecuaciones diferenciales ordinarias. Es importante recalcar la condición de adimensionalidad que obliga a incorporar las velocidades iniciales de lanzamiento en la constante de adimensionalización. Así los sistemas serán
| > |
sist1 := subs([omega0=2,phi0=3.5,tfinal=10],diff(theta(t),t)=phi0*tfinal*phi(t)),
subs([omega0=2,phi0=3.5,tfinal=10],diff(phi(t),t)=-((omega0^2*tfinal)/phi0)*sin(theta(t)));
sist2 := subs([omega0=2,phi0=3.9,tfinal=10],diff(theta(t),t)=phi0*tfinal*phi(t)),
subs([omega0=2,phi0=3.9,tfinal=10],diff(phi(t),t)=-((omega0^2*tfinal)/phi0)*sin(theta(t)));
sist3 := subs([omega0=2,phi0=4,tfinal=10],diff(theta(t),t)=phi0*tfinal*phi(t)),
subs([omega0=2,phi0=4,tfinal=10],diff(phi(t),t)=-((omega0^2*tfinal)/phi0)*sin(theta(t)));
sist4 := subs([omega0=2,phi0=4.1,tfinal=10],diff(theta(t),t)=phi0*tfinal*phi(t)),
subs([omega0=2,phi0=4.1,tfinal=10],diff(phi(t),t)=-((omega0^2*tfinal)/phi0)*sin(theta(t)));
sist5 := subs([omega0=2,phi0=4.5,tfinal=10],diff(theta(t),t)=phi0*tfinal*phi(t)),
subs([omega0=2,phi0=4.5,tfinal=10],diff(phi(t),t)=-((omega0^2*tfinal)/phi0)*sin(theta(t)));
funs := {theta(t), phi(t)};
soluc1:= dsolve({sist1,theta(0)=0,phi(0)=1},funs,type=numeric,abserr=0.00001):
soluc2:= dsolve({sist2,theta(0)=0,phi(0)=1},funs,type=numeric,abserr=0.00001):
soluc3:= dsolve({sist3,theta(0)=0,phi(0)=1},funs,type=numeric,abserr=0.00001):
soluc4:= dsolve({sist4,theta(0)=0,phi(0)=1},funs,type=numeric,abserr=0.00001):
soluc5:= dsolve({sist5,theta(0)=0,phi(0)=1},funs,type=numeric,abserr=0.00001):
graf1:=odeplot(soluc1, [t,theta(t)], 0..1, numpoints=50):
graf2:=odeplot(soluc2, [t,theta(t)], 0..1, numpoints=50):
graf3:=odeplot(soluc3, [t,theta(t)], 0..1, numpoints=50):
graf4:=odeplot(soluc4, [t,theta(t)], 0..1, numpoints=50):
graf5:=odeplot(soluc5, [t,theta(t)], 0..1, numpoints=50):
graf10:=odeplot(soluc1, [theta(t),phi(t)], 0..1, numpoints=50):
graf20:=odeplot(soluc2, [theta(t),phi(t)], 0..1, numpoints=50):
graf30:=odeplot(soluc3, [theta(t),phi(t)], 0..1, numpoints=50):
graf40:=odeplot(soluc4, [theta(t),phi(t)], 0..1, numpoints=50):
graf50:=odeplot(soluc5, [theta(t),phi(t)], 0..1, numpoints=50):
|
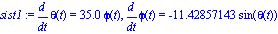
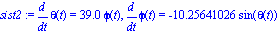
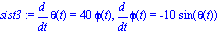
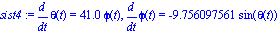
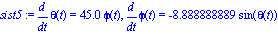
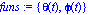
Las cuales se integran numericamete y proveen las siguientes gráficas
| > |
display([graf1,graf2,graf3,graf4,graf5],view=[0..1,-2*Pi..2*Pi]);
display([graf10,graf20,graf30,graf40,graf50],scaling=constrained,view=[-5..5,-2..2]); |
![[Plot]](simulacionesimag/Simulaciones_165.gif)
![[Plot]](simulacionesimag/Simulaciones_166.gif)
Un Ejemplo en Relatividad General
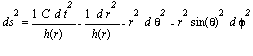
 = rho(r)-2*Int(zeta^2*rho(zeta), zeta = (0 .. r))/r^3](simulacionesimag/Simulaciones_168.gif)
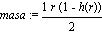 ,
,
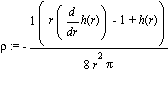 ,
, 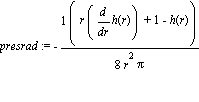 y
y 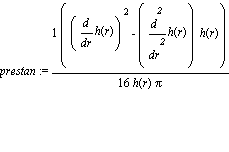
Ejemplo 7 Ptan = 0 y Prad <> 0
| > |
restart;with(plots):Digits:=30: |
Warning, the name changecoords has been redefined
Este procedimiento calcula los ceros de una ecuacion trascendente, cuyos ceros se encuentran entre 0 y 1 y los grafica
| > |
graficadeceros:=proc(param_inicial, param_final, n_param, funcion, parametro,Lista_puntos)
local funcion_local,var_cero,delta_param,Lista,var_maxima,a_param,imax,i,punto;
delta_param:= (param_final-param_inicial)/n_param;
a_param[1]:=param_inicial;
Lista:=[];
var_maxima:=0.000001;
for i from 1 to n_param
do
funcion_local:=subs(parametro=a_param[i],funcion);
var_cero:=fsolve(funcion_local,zeta=0..1):
punto[i]:=[a_param[i],var_cero];
Lista:=[op(Lista),punto[i]];
if var_cero > var_maxima
then var_maxima:= var_cero;
imax:=i
end if:
a_param[i+1]:=a_param[i] +delta_param:
end do;
with(plots):
Lista_puntos:=Lista;
print(plot(Lista,labels=["M/R","zeta"]));
print("var maxima =",var_maxima,"M/R =",a_param[imax]);
end proc: |
| > |
h:=r-> xi*exp((-1+xi)*(r-R)/R/xi); |
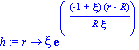
| > |
assume(R,positive,R,real);assume(xi>0,xi<1);assume(zeta>0,zeta<1); |
h(r) en latex
Las derivadas de h(r)
| > |
#diffache:=diff(h(r),r);grafdiffache:=R*simplify(subs([r=zeta*R],diffache)); |
| > |
#animate(grafdiffache,zeta=0.01..1,xi=0.01..1,frames=50,title="diffache",view=-10..10); |
| > |
#diff2ache:=diff(h(r),r,r); grafdiff2ache:=R^2*simplify(subs([r=zeta*R],diff2ache)); |
| > |
#animate(grafdiff2ache,zeta=0.01..1,xi=0.01..1,frames=50,title="diff2ache",view=-10..10); |
Ahora se chequean las condiciones de aceptabilidad fisica del fluido
En las variables fisicas. Primero se chequea la consistencia de la entrada de datos..... de lo calculado a lo e
| > |
rho := simplify(-1/8*(r*diff(h(r),r)-1+h(r))/r^2/Pi);
rho:=collect(%,[exp,r]);
#latex(%);
Limit(rho,r=0)=limit(rho,r=0); |
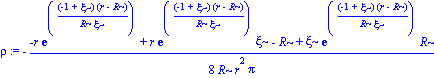
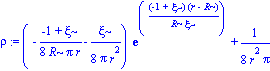
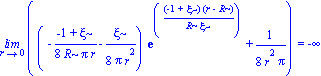
| > |
grafrho:=R^2*simplify(subs([r=zeta*R],rho)):
grafrho:=collect(%,exp);
grafrhoMR:=simplify(subs(xi=1-2*MR,grafrho)):
grafrhoMR:=collect(%,exp);
|
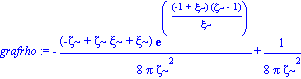
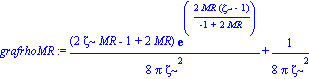
Existe un entorno, cercano al centro de la distribucion para el cual la densidad es negativa
en este aparte se determina los valores para el potencial gravitacional en la superficie xi que generan
un nucleo en el cual no se cumplen las condiciones de energia. En particular se presenta una grafica
de estos valores de zeta (la variable radial) para la cual el gradiente de densidades comienza a ser
negativo el valor de ese entorno es zeta 0.33157608318035639063
| > |
funcion:=simplify(zeta^2*Pi*grafrhoMR)=0;
MR_inicial:=0.01;MR_final:=0.5;n_MR:=100;
graficadeceros(MR_inicial, MR_final, n_MR,funcion,MR,Lista_puntosrho); |


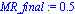
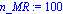
![[Plot]](simulacionesimag/Simulaciones_183.gif)

| > |
#Lista_puntosrho;Lista_puntosrho[6];zeta1:=op(1,Lista_puntosrho[6]);MR1:=op(2,Lista_puntosrho[6]); |
| > |
grafrho015:=subs(xi=.150,grafrho):
grafrhomax:=subs(xi=.25075000000000000000,grafrho):
grafrho04:=subs(xi=.4,grafrho):
grafrho06:=subs(xi=.6,grafrho):
grafrho08:=subs(xi=.8,grafrho):
plot([grafrho015,grafrhomax,grafrho04,grafrho06,grafrho08],zeta=0.01..1,title="rho > 0",legend=["xi = 0.15","xi max","xi = 0.4","xi = 0.6","xi = 0.8"],view=-1..1);
plot(grafrhomax,zeta=0.01..1,title="rho xi max > 0",view=-1..1); |
![[Plot]](simulacionesimag/Simulaciones_185.gif)
![[Plot]](simulacionesimag/Simulaciones_186.gif)
| > |
presrad:=simplify(1/8*(-r*diff(h(r),r)-1+h(r))/r^2/Pi):
presrad:=collect(%,[exp,r]);
#latex(%);
Limit(presrad,r=0)=limit(presrad,r=0); |
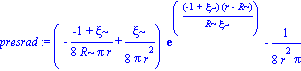
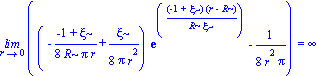
| > |
grafpresrad:=R^2*simplify(subs([r=zeta*R],presrad)):
grafpresrad015:=subs(xi=.15,grafpresrad):
grafpresrad025:=subs(xi=.25,grafpresrad):
grafpresrad04:=subs(xi=.4,grafpresrad):
grafpresrad06:=subs(xi=.6,grafpresrad):
grafpresrad08:=subs(xi=.8,grafpresrad):
plot([grafpresrad015,grafpresrad025,grafpresrad04,grafpresrad06,grafpresrad08],zeta=0.01..1,title="presion radial > 0",legend=["xi = 0.15","xi 0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=0..1); |
![[Plot]](simulacionesimag/Simulaciones_189.gif)
| > |
prestan := simplify(-1/16*(-diff(h(r),r)^2+diff(h(r),`$`(r,2))*h(r))/h(r)/Pi); |

| > |
grafprestan:=prestan;
Delta :=simplify((grafprestan-grafpresrad)/zeta):Delta:=collect(%,exp);
Delta015:=subs(xi=.15,Delta):
Delta025:=subs(xi=.25,Delta):
Delta04:=subs(xi=.4,Delta):
Delta06:=subs(xi=.6,Delta):
Delta08:=subs(xi=.8,Delta):
plot([Delta015,Delta025,Delta04,Delta06,Delta08],zeta=0.01..1,title="Delta",legend=["xi = 0.15","xi 0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=-10..0); |

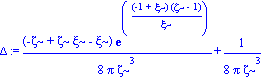
![[Plot]](simulacionesimag/Simulaciones_193.gif)
En los gradientes de las variables fisicas
| > |
difrho:=simplify(diff(rho,r));
grafdifrho:=R^3*simplify(subs([r=zeta*R],difrho)):
grafdifrho:=collect(%,exp);
grafdifrhoMR:=simplify(subs(xi=1-2*MR,grafdifrho)):
grafdifrhoMR:=collect(simplify(%),exp);
|
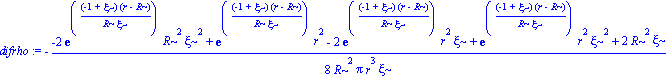
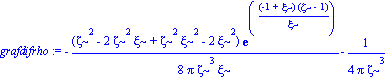
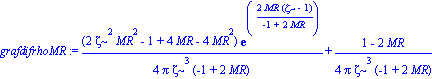
| > |
funcion:=simplify((-1+2*MR)*Pi*zeta^3*grafdifrhoMR):funcion:=collect(%,exp);
MR_inicial:=0.01;MR_final:=0.5;n_MR:=100;
graficadeceros(MR_inicial, MR_final, n_MR,funcion,MR,Lista_puntosdiffrho); |
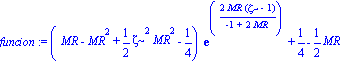

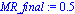
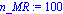
![[Plot]](simulacionesimag/Simulaciones_201.gif)

| > |
#plot([Lista_puntosdiffrho,Lista_puntosrho],labels=["M/R","zeta"],legend=["diffrho","rho"]); |
| > |
grafdifrho015:=subs(xi=.15,grafdifrho):
grafdifrho025:=subs(xi=.25,grafdifrho):
grafdifrho04:=subs(xi=.4,grafdifrho):
grafdifrho06:=subs(xi=.6,grafdifrho):
grafdifrho08:=subs(xi=.8,grafdifrho):
plot([grafdifrho015,grafdifrho025,grafdifrho04,grafdifrho06,grafdifrho08],zeta=.33158317799315922767..1,title="difrho < 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=-1..0);
|
![[Plot]](simulacionesimag/Simulaciones_203.gif)
Por lo tanto repetimos todas las graficas anteriores para valores zeta <=.33158317799315922767
| > |
plot([grafrho015,grafrhomax,grafrho04,grafrho06,grafrho08],zeta=.33158317799315922767..1,title="rho > 0",legend=["xi = 0.15","xi max","xi = 0.4","xi = 0.6","xi = 0.8"],view=0..1);
plot([grafpresrad015,grafpresrad025,grafpresrad04,grafpresrad06,grafpresrad08],zeta=.33158317799315922767..1,title="presion radial > 0",legend=["xi = 0.15","xi 0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=0..1);
plot([Delta015,Delta025,Delta04,Delta06,Delta08],zeta=.33158317799315922767..1,title="Delta",legend=["xi = 0.15","xi 0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=-1..0);
plot([grafdifrho015,grafdifrho025,grafdifrho04,grafdifrho06,grafdifrho08],zeta=.33158317799315922767..1,title="difrho < 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=-1..0);
|
![[Plot]](simulacionesimag/Simulaciones_204.gif)
![[Plot]](simulacionesimag/Simulaciones_205.gif)
![[Plot]](simulacionesimag/Simulaciones_206.gif)
![[Plot]](simulacionesimag/Simulaciones_207.gif)
| > |
difpresrad:=simplify(diff(presrad,r)):
difpresrad:=collect(%,exp); |
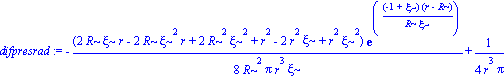
| > |
grafdifpresrad:=R^3*simplify(subs([r=zeta*R],difpresrad)):
grafdifpresrad015:=subs(xi=.15,grafdifpresrad):
grafdifpresrad025:=subs(xi=.25,grafdifpresrad):
grafdifpresrad04:=subs(xi=.4,grafdifpresrad):
grafdifpresrad06:=subs(xi=.6,grafdifpresrad):
grafdifpresrad08:=subs(xi=.8,grafdifpresrad):
plot([grafdifpresrad015,grafdifpresrad025,grafdifpresrad04,grafdifpresrad06,grafdifpresrad08],zeta=.33158317799315922767..1,title="difpresrad < 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=-1..0);
|
![[Plot]](simulacionesimag/Simulaciones_209.gif)
Las velocidades del sonido de forma directa, a traves de los gradientes de las variables fisicas
| > |
velsonrad:= collect(simplify(difpresrad/difrho),exp);
grafvelsonrad :=simplify(subs([r=zeta*R],velsonrad)):collect(%,exp);
grafvelsonrad015:=subs(xi=.15,grafvelsonrad):
grafvelsonrad025:=subs(xi=.25,grafvelsonrad):
grafvelsonrad04:=subs(xi=.4,grafvelsonrad):
grafvelsonrad07:=subs(xi=.7,grafvelsonrad):
grafvelsonrad08:=subs(xi=.8,grafvelsonrad):
plot([grafvelsonrad015,grafvelsonrad025,grafvelsonrad04,grafvelsonrad07,grafvelsonrad08],zeta=.33158317799315922767..1,title="grafvelsonrad > 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.7","xi = 0.8"],view=0..1);
|
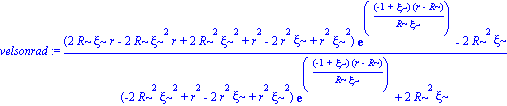
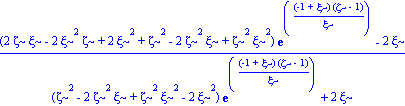
![[Plot]](simulacionesimag/Simulaciones_212.gif)
| > |
#graflimitvelsonrad:=collect(subs(zeta=.33158317799315922767,grafvelsonrad),exp);
#xi_comienzo:=fsolve(graflimitvelsonrad-1,xi=0.6..0.8);
#MR_comienzo:=(1-xi_comienzo)/2;
#plot(graflimitvelsonrad,xi=0..1,view=0..1); |
| > |
velson_1:=simplify(grafvelsonrad-1);
#velson_1:=collect(subs(xi=1-2*MR,%),exp);
funcion:=numer(velson_1):funcion:=collect(%,exp);
xipave:=fsolve(subs(zeta=.33158317799315922767,velson_1),xi=0..1);
MR_inicial:=0.001;n_MR:=100;
#graficadeceros(MR_inicial, MR_final, n_MR,funcion,MR,Lista_velson1);
|
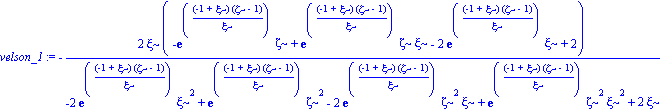
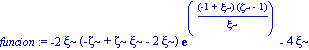

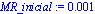
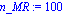
| > |
grafvelsonrad069:=subs(xi=0.69395986785397797260,grafvelsonrad):
grafvelsonrad075:=subs(xi=.75,grafvelsonrad):
grafvelsonrad08:=subs(xi=.8,grafvelsonrad):
grafvelsonrad085:=subs(xi=.85,grafvelsonrad):
grafvelsonrad090:=subs(xi=.9,grafvelsonrad):
plot([grafvelsonrad069,grafvelsonrad075,grafvelsonrad08,grafvelsonrad085,grafvelsonrad09],zeta=.33158317799315922767..1,title="grafvelsonrad > 0",legend=["xi = 0.6939","xi =0.75","xi = 0.8","xi = 0.85","xi = 0.9"],view=0..1); |
Warning, unable to evaluate 1 of the 5 functions to numeric values in the region; see the plotting command's help page to ensure the calling sequence is correct
![[Plot]](simulacionesimag/Simulaciones_218.gif)
Notese que se restringieron los valores de xi y que no es posible tener una velocidad del sonido tangencial...
La Condicion de energia Fuerte
| > |
fuerte := -1/8/r*(-diff(h(r),r)^2*r+diff(h(r),`$`(r,2))*h(r)*r+2*diff(h(r),r)*h(r))/Pi/h(r);
graffuerte:=R^2*simplify(subs([r=zeta*R],fuerte)): |
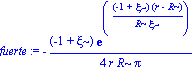
| > |
graffuerte015:=subs(xi=.15,graffuerte):
graffuerte025:=subs(xi=.25,graffuerte):
graffuerte04:=subs(xi=.4,graffuerte):
graffuerte06:=subs(xi=.6,graffuerte):
graffuerte08:=subs(xi=.8,graffuerte):
plot([graffuerte015,graffuerte025,graffuerte04,graffuerte06,graffuerte08],zeta=.33158317799315922767..1,title="fuerte > 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=0..5);
|
![[Plot]](simulacionesimag/Simulaciones_220.gif)
| > |
animate(graffuerte,zeta=0.33157608318035639063..1,xi=0.7..0.95,frames=50,title="Condicion Energia Fuerte > 0",view=0..0.2); |
![[Plot]](simulacionesimag/Simulaciones_221.gif)
| > |
fuertetan := -1/16*(2*h(r)*r*diff(h(r),r)-2*h(r)+2*h(r)^2-diff(h(r),r)^2*r^2+diff(h(r),`$`(r,2))*h(r)*r^2)/r^2/Pi/h(r);
graffuertetan:=R^2*simplify(subs([r=zeta*R],fuertetan)); |
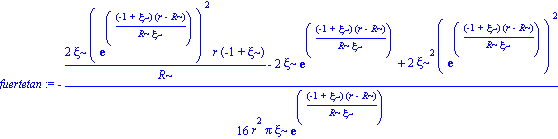
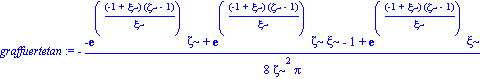
| > |
graffuertetan015:=subs(xi=.15,graffuertetan):
graffuertetan025:=subs(xi=.25,graffuertetan):
graffuertetan04:=subs(xi=.4,graffuertetan):
graffuertetan06:=subs(xi=.6,graffuertetan):
graffuertetan08:=subs(xi=.8,graffuertetan):
plot([graffuertetan015,graffuertetan025,graffuertetan04,graffuertetan06,graffuertetan08],zeta=.33158317799315922767..1,title="fuertetan > 0",legend=["xi = 0.15","xi =0.25","xi = 0.4","xi = 0.6","xi = 0.8"],view=0..3);
|
![[Plot]](simulacionesimag/Simulaciones_224.gif)
| > |
#animate(graffuertetan,zeta=0.33157608318035639063..1,xi=0.7..0.85,frames=50,title="Condicion Energia Fuerte tangencial > 0",view=0..0.1); |
La Funcion Masa y la Masa de Tolman Whitakker.
| > |
masa:=(1-h(r))*(r/2);
mtw:= simplify(((1-2*(R/2)*(1-xi)/R)/h(r))*(masa +4*Pi*r^3*presrad)); |
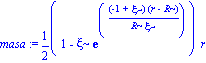
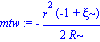
La masa de tolman whitakker en latex
| > |
#latex(mtw);latex(masa); |
| > |
grfmasa:=simplify(subs([r=zeta*R],masa)/R);
grfmtw:=simplify(subs([r=zeta*R],mtw)/R); |
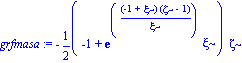
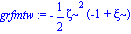
| > |
animate({grfmasa,grfmtw},zeta=0.33157608318035639063..1,xi=0.7..0.95,frames=50,title="masa & mtw",view=0..0.2); |
![[Plot]](simulacionesimag/Simulaciones_229.gif)
===============================================================================
Investigación Gráfica de la Cardiode
Por Francis J. Wright, January 2003, basado en un trabajo "White-Box/Black-Box revisited" by P. Drijvers, The International DERIVE Journal, 1995, Vol. 2, No. 1, 3?14.
![]() 0 la densidad del fluido y
0 la densidad del fluido y ![]() 1 la densidad del cuerpo (gotas/balas/conchos/burbujas) en Kilogramos/
1 la densidad del cuerpo (gotas/balas/conchos/burbujas) en Kilogramos/![]()
![]() R y
R y ![]() es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg /
es el coeficiente de fricción que depende de la viscosidad del fluido. En el sistema MKS se expresa en N sg /![]() y se mide en Poise que es igual a un décimo de la unidad en MKS.
y se mide en Poise que es igual a un décimo de la unidad en MKS.![]()
![]()
![]()
![]()
![]() y
y ![]() representan las densidades relativas del fluido y del cuerpo respecto al agua (de densidad
representan las densidades relativas del fluido y del cuerpo respecto al agua (de densidad ![]() ), respectivamente.
), respectivamente.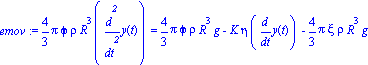
![]()
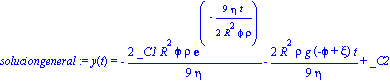
![]() ,
,![]() ,
,![]() y
y ![]() . Estas cantidades nos permiten modelar el fenómeno.
. Estas cantidades nos permiten modelar el fenómeno.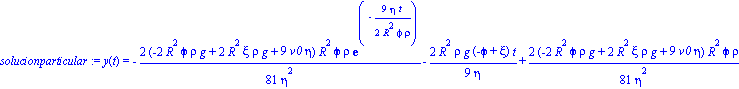
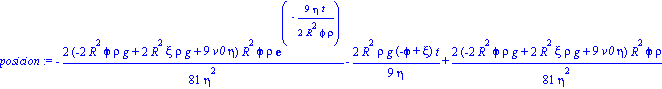
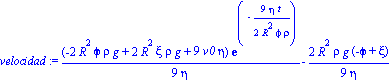
![]()
![]()
![]()
![]()
![[Plot]](simulacionesimag/Simulaciones_28.gif)
![]()
![[Plot]](simulacionesimag/Simulaciones_30.gif)
![[Plot]](simulacionesimag/Simulaciones_31.gif)
![[Plot]](simulacionesimag/Simulaciones_32.gif)
![]()
![]()
![]()
![]()
![]()
![[Plot]](simulacionesimag/Simulaciones_38.gif)
![]()
![[Plot]](simulacionesimag/Simulaciones_40.gif)
![[Plot]](simulacionesimag/Simulaciones_41.gif)
![[Plot]](simulacionesimag/Simulaciones_42.gif)
![[Plot]](simulacionesimag/Simulaciones_43.gif)
![[Plot]](simulacionesimag/Simulaciones_44.gif)
![[Plot]](simulacionesimag/Simulaciones_45.gif)
![[Plot]](simulacionesimag/Simulaciones_46.gif)
![[Plot]](simulacionesimag/Simulaciones_47.gif)
![[Plot]](simulacionesimag/Simulaciones_48.gif)
![]()
![]()
![[Plot]](simulacionesimag/Simulaciones_51.gif)
![]()
![[Plot]](simulacionesimag/Simulaciones_53.gif)
![[Plot]](simulacionesimag/Simulaciones_54.gif)
![[Plot]](simulacionesimag/Simulaciones_55.gif)
![]()
![]()
![]()
![]()
![]()
![]()
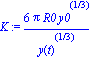
![]() y
y ![]() representan las densidad relativas del fluido y del cuerpo respecto al agua (de densidad
representan las densidad relativas del fluido y del cuerpo respecto al agua (de densidad ![]() ), respectivamente. Por su parte
), respectivamente. Por su parte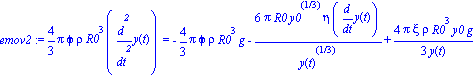
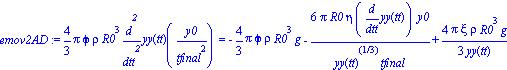
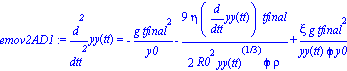
![]() = pp(tt) con lo cual
= pp(tt) con lo cual ![]() =
= ![]()
![]()
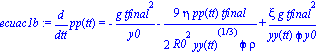
![]()
![]()
![]()
![]()
![[Plot]](simulacionesimag/Simulaciones_78.gif)
![[Plot]](simulacionesimag/Simulaciones_79.gif)
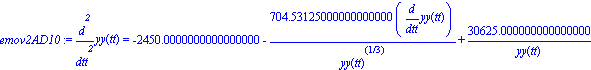
![]()
![[Plot]](simulacionesimag/Simulaciones_82.gif)
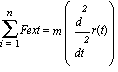
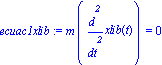
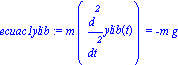
![[Plot]](simulacionesimag/Simulaciones_88.gif)
![U[v] = V[x]*i/(V[x]^2+V[y]^2)^(1/2)+V[y]*j/(V[x]^2+V[y]^2)^(1/2)](simulacionesimag/Simulaciones_94.gif) y
y 
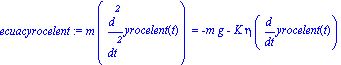
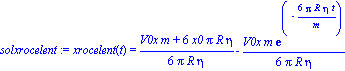
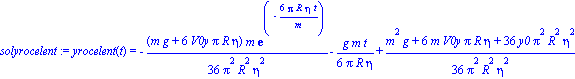
![[Plot]](simulacionesimag/Simulaciones_103.gif)
![[Plot]](simulacionesimag/Simulaciones_104.gif)
![[Plot]](simulacionesimag/Simulaciones_105.gif)
![[Plot]](simulacionesimag/Simulaciones_106.gif)
![[Plot]](simulacionesimag/Simulaciones_107.gif)
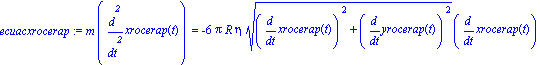
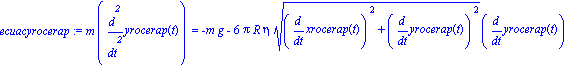
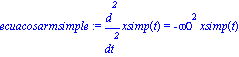
![[Plot]](simulacionesimag/Simulaciones_120.gif)
![[Plot]](simulacionesimag/Simulaciones_121.gif)
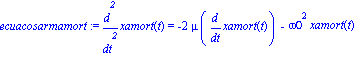
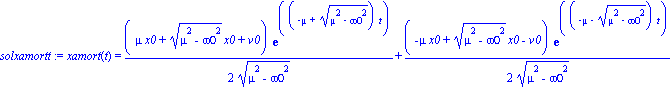
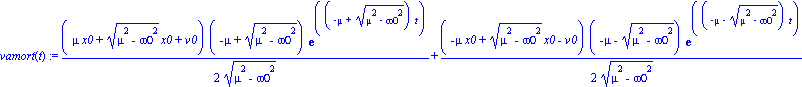
![[Plot]](simulacionesimag/Simulaciones_133.gif)
![[Plot]](simulacionesimag/Simulaciones_134.gif)
![[Plot]](simulacionesimag/Simulaciones_136.gif)
![[Plot]](simulacionesimag/Simulaciones_137.gif)
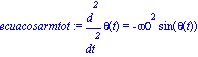
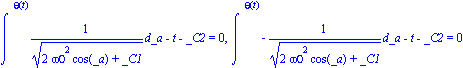
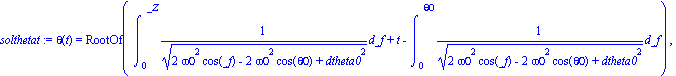

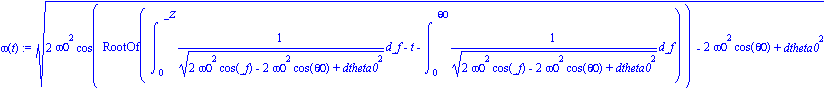
![[Plot]](simulacionesimag/Simulaciones_146.gif)
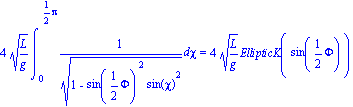
![matrix([[2.838453791, 1/12*pi, 1/6*pi, 1/4*pi, 1/3*pi, 1/2*pi, 2/3*pi], [](simulacionesimag/Simulaciones_150.gif)
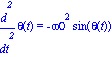
![[Plot]](simulacionesimag/Simulaciones_165.gif)
![[Plot]](simulacionesimag/Simulaciones_166.gif)
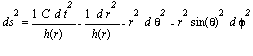
 = rho(r)-2*Int(zeta^2*rho(zeta), zeta = (0 .. r))/r^3](simulacionesimag/Simulaciones_168.gif)
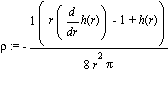 ,
, 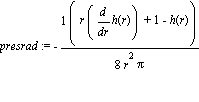 y
y 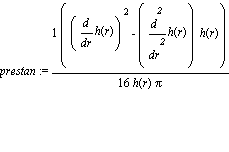
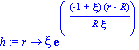
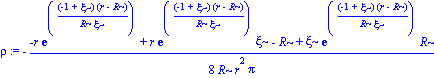
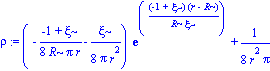
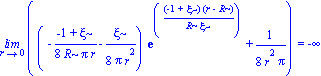
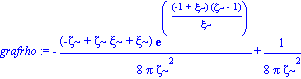
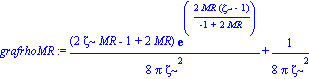

![[Plot]](simulacionesimag/Simulaciones_183.gif)
![[Plot]](simulacionesimag/Simulaciones_185.gif)
![[Plot]](simulacionesimag/Simulaciones_186.gif)
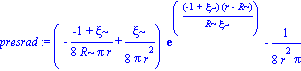
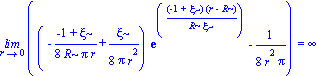
![[Plot]](simulacionesimag/Simulaciones_189.gif)
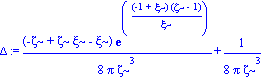
![[Plot]](simulacionesimag/Simulaciones_193.gif)
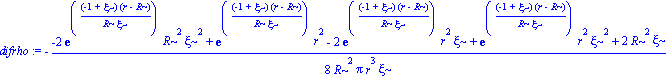
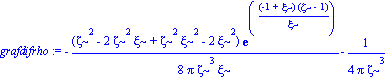
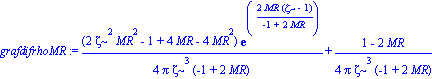
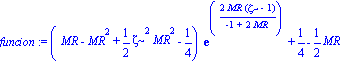
![[Plot]](simulacionesimag/Simulaciones_201.gif)
![[Plot]](simulacionesimag/Simulaciones_203.gif)
![[Plot]](simulacionesimag/Simulaciones_204.gif)
![[Plot]](simulacionesimag/Simulaciones_205.gif)
![[Plot]](simulacionesimag/Simulaciones_206.gif)
![[Plot]](simulacionesimag/Simulaciones_207.gif)
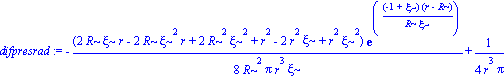
![[Plot]](simulacionesimag/Simulaciones_209.gif)
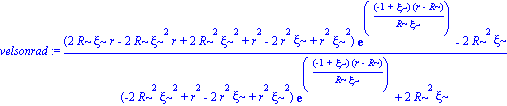
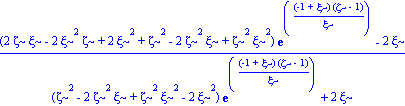
![[Plot]](simulacionesimag/Simulaciones_212.gif)
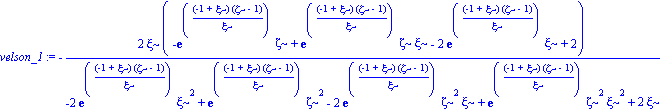
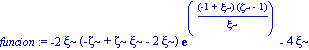
![[Plot]](simulacionesimag/Simulaciones_218.gif)
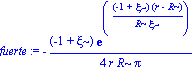
![[Plot]](simulacionesimag/Simulaciones_220.gif)
![[Plot]](simulacionesimag/Simulaciones_221.gif)
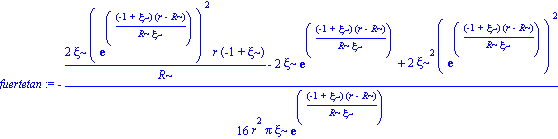
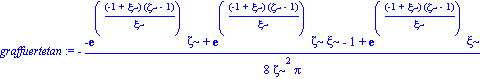
![[Plot]](simulacionesimag/Simulaciones_224.gif)
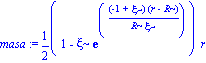
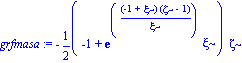
![[Plot]](simulacionesimag/Simulaciones_229.gif)