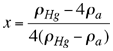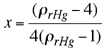|
|
Ir arriba |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Problema 1 |
|
|
|
|
|
Datos |
|
|
Pregunta |
|
|
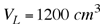 Volumen de la lata. Volumen de la lata.
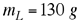 Masa de la lata. Masa de la lata.
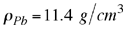 Densidad del plomo. Densidad del plomo.
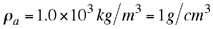 Densidad del agua. Densidad del agua.
|
|
|
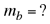
masa de balas de plomo que se pueden colocar en la lata de estaño sin que ésta se hunda. |
|
| |
Solución |
|
| |
Para que la lata no se hunda cuando se colocan en su interior balas de plomo, se debe cumplir que |
|
| |
|
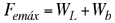 |
(1) |
|
| |
Donde 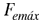 Fuerza de empuje máxima que puede experimentar la lata. Fuerza de empuje máxima que puede experimentar la lata.
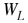 Peso de la lata. Peso de la lata.
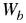 Peso de las balas de plomo. Peso de las balas de plomo.
Puesto que la fuerza de empuje es igual al peso del fluido desalojado por la lata tenemos que |
|
| |
|
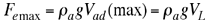 |
(2) |
|
| |
Donde 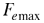 fuerza de empuje máxima. fuerza de empuje máxima.
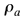 densidad del agua. densidad del agua.
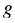 aceleración de gravedad. aceleración de gravedad.
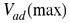 volumen máximo de agua desalojada por la lata. volumen máximo de agua desalojada por la lata.
Reemplazando la expresión (2) en (1) se obtiene que 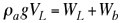
de donde se obtiene para la masa máxima de balas de plomo que se pueden colocar en la lata |
|
| |
|
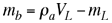 |
(3) |
|
| |
Reemplazando los valores numéricos correspondiente en la expresión (3) se tiene |
|
| |
|
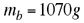 |
|
|
| |
En el interior de la lata se puede colocar un máximo de 1070 g de balas de plomo sin que esta se hunda. |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Consulta al Profesor |
Consulta al Grupo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ir arriba |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Problema 2 |
|
|
Un cubo que está flotando en mercurio tiene sumergida la cuarta parte de su volumen. Si se agrega agua suficiente para cubrir el cubo, ¿qué fracción de su volumen quedará sumergida en el mercurio? ¿La respuesta depende de la forma del cuerpo? Considere la densidad relativa del mercurio 13.6. |
|
|
Datos |
|
Pregunta |
|
|
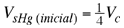
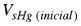
Volumen inicial del cubo sumergido en mercurio. 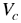
Volumen del cubo. |
|
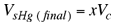
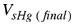
Volumen final del cubo sumergido en mercurio. 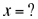
Fracción del volumen del cubo. |
|
|
Solución |
|
|
Representación gráfica de las situaciones físicas planteadas en el enunciado del problema. Dibujo Tenemos que en ambas situaciones para que el cubo flote se debe cumplir que
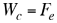 (1) (1)
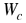 peso del cubo. peso del cubo.
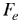 fuerza de empuje. fuerza de empuje.
a) Análisis de la situación inicial. Tenemos que la fuerza de empuje se puede expresar como |
|
|
|
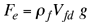 |
|
|
|
donde 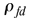 Densidad del fluido desalojado. Densidad del fluido desalojado. 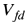 Volumen del fluido desalojado. Volumen del fluido desalojado.
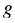 Aceleración de gravedad. Aceleración de gravedad.
Se tiene entonces que el empuje en la situación inicial está dado por |
|
|
|
 |
(2) |
|
|
Donde 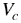 volumen del cubo. volumen del cubo. 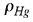 densidad del mercurio. densidad del mercurio.
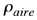 densidad del aire. densidad del aire.
Puesto que la densidad del mercurio 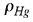 es mucho mayor que la del aire es mucho mayor que la del aire 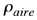 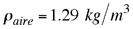 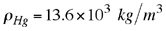
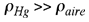
en la expresión (2) podemos despreciar el segundo término con lo cual tenemos para la fuerza de empuje 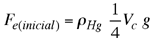 (3) (3) Reemplazando (3) en (1) tenemos que el peso del cubo está dado por la siguiente expresión 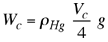 (4) (4) b) Análisis de la situación final. Analicemos ahora la situación final planteada en Dibujo, tenemos que en este caso la fuerza de empuje está dada por |
|
|
|
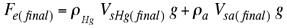 |
(5) |
|
|
Donde 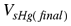 Volumen final del cubo sumergido en mercurio. Volumen final del cubo sumergido en mercurio.
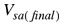 Volumen final del cubo sumergido en agua. Volumen final del cubo sumergido en agua.
Reemplazando (5) en (1) tenemos: 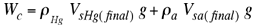 (6) (6)
igualando (4) y (6) se obtiene  (7) (7) Considerando que 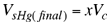
y por lo tanto |
|
|
|
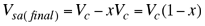 |
|
|
|
tenemos que la expresión (7) se puede escribir como 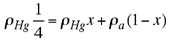
de donde se obtiene que |
|
|
|
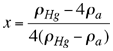 |
|
|
|
considerando que 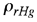 es la densidad relativa del mercurio se obtiene. es la densidad relativa del mercurio se obtiene. |
|
|
|
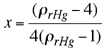 |
|
|
|
reemplazando los valores correspondientes tenemos 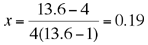
Este valor no depende de la forma del cuerpo. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Consulta al Profesor |
Consulta al Grupo |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ir arriba |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() y una masa de
y una masa de ![]() . ¿Cuántos gramos máximos de balas de plomo podría llevar sin hundirse en el agua? La densidad del plomo es de
. ¿Cuántos gramos máximos de balas de plomo podría llevar sin hundirse en el agua? La densidad del plomo es de ![]() .
.