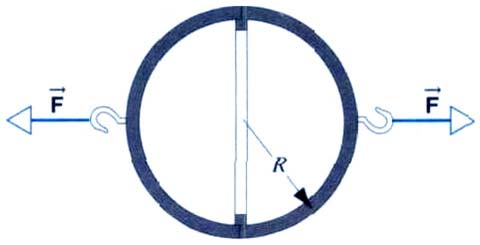
La presión atmosférica ejerce sobre los hemisferios fuerzas que apuntan radialmente hacia el centro de ellos.
De igual manera el aire contenido dentro de los hemisferios ejerce fuerzas sobre la superficie interna en dirección radial y sentido saliente.
Por lo tanto sobre cada uno de los hemisferios actúa una fuerza resultante 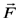 . .
Para realizar el desarrollo del problema introducimos un sistema de coordenadas, centrado en la esfera que forman ambos hemisferios y cuyo eje y es perpendicular a la unión entre ellos (plano xz). Ver Fig.1
En dicho sistema de coordenadas se puede definir un elemento de superficie del casquete esférico el cual está dado por expresión (1) . Ver Fig. 2
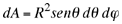 (1) (1)
Las fuerzas internas 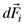 y externas y externas 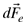 que actúan sobre cada elemento de superficie que actúan sobre cada elemento de superficie 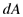 se pueden descomponer en el sistemas de coordenadas elegido. se pueden descomponer en el sistemas de coordenadas elegido.
Consideremos el hemisferio de la derecha y dibujemos sobre él, el elemento de fuerza 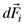 , esta fuerza es radial y saliente de cada elemento de superficie. Ver Fig. 3. , esta fuerza es radial y saliente de cada elemento de superficie. Ver Fig. 3.
La fuerza total 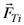 que actúa sobre la superficie interna del hemisferio derecho está dada por que actúa sobre la superficie interna del hemisferio derecho está dada por
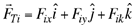 (2) (2)
Donde
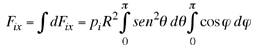 (3) (3)
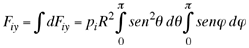 (4) (4)
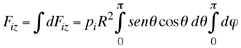 (5) (5)
A partir de la expresión (3) se tiene que
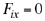 (6) (6)
A partir de la expresión (5) se tiene que
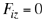 (7) (7)
A partir de la expresión (4) se obtiene que
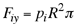 (8) (8)
Reemplazando los valores de 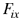 , , 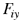 y y 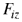 en la expresión (2) se tiene que la fuerza total que actúa sobre la superficie interna del hemisferio derecho está dada por en la expresión (2) se tiene que la fuerza total que actúa sobre la superficie interna del hemisferio derecho está dada por
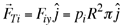 (9) (9)
Calculemos de forma similar la fuerza que la atmósfera, ejerce sobre la superficie externa del hemisferio derecho. Esta fuerza es radial y entrante a cada elemento de superficie, la denominamos 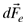 con la componente radial con la componente radial
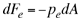
en donde el signo negativo indica su carácter de entrante.
Tenemos por lo tanto en este caso que
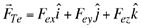
donde
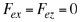
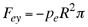
Por lo tanto
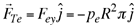 (10) (10)
Se tiene entonces que la fuerza resultante que actúa sobre el hemisferio derecho está dada por
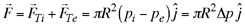 (11) (11)
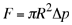 (12) (12)
Comentario |
![]() ,donde R es el radio (exterior) de las semiesferas, y
,donde R es el radio (exterior) de las semiesferas, y ![]() es la diferencia de presión en el exterior e interior de la esfera, ver fig. b) Si suponemos que R es igual a 0.305 m y la presión interna es 0.100 atm, ¿qué fuerza debería ejercer el tiro para separar las semiesferas?
es la diferencia de presión en el exterior e interior de la esfera, ver fig. b) Si suponemos que R es igual a 0.305 m y la presión interna es 0.100 atm, ¿qué fuerza debería ejercer el tiro para separar las semiesferas?