


Next: About this document ...
Problemario 1
Prof. W. Barreto
Octubre 26, 2007
- Demostrar que el producto vectorial entre dos vectores
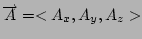 y
y
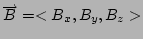 se puede calcular a través de un determinante.
se puede calcular a través de un determinante.
- Comprobar que
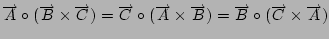
- Comprobar que
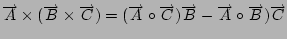
- Demuestre el Teorema del Coseno usando vectores
- Demuestre el Teorema del Seno usando vectores
- Demuestre la identidad trigonométrica
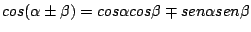 , usando vectores.
, usando vectores.
- Demuestre la identidad trigonométrica
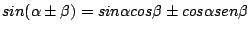 , usando vectores.
, usando vectores.
- Encuentre la relación entre la triada de vectores ortonormales cartesianos y la triada de vectores ortonormales en coordenadas esféricas.
- Encuentre la relación entre la triada de vectores ortonormales cartesianos y la triada de vectores ortonormales en coordenadas cilíndricas.
- Represente el vector
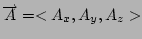 como una combinación lineal de la base ortonormal en coordenadas cartesianas, esféricas y
cilíndricas.
como una combinación lineal de la base ortonormal en coordenadas cartesianas, esféricas y
cilíndricas.
Willians Barreto
2007-10-30