


Next: About this document ...
Problemario 2 (Parte I)
Prof. W. Barreto
Noviembre 2, 2007
- Demostrar que para el movimiento uniformemente acelerado las siguientes dos ecuaciones
son equivalentes:
- Para el movimiento circular de radio
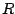 y usando coordenadas cilíndricas, demuestre que la aceleración tiene componentes tangencial y normal:
y usando coordenadas cilíndricas, demuestre que la aceleración tiene componentes tangencial y normal:
donde la velocidad tangencial es 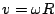 ,
,
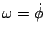 es la velocidad angular, y
es la velocidad angular, y
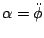 es la aceleración angular.
Demuestre también que para el movimiento circular:
es la aceleración angular.
Demuestre también que para el movimiento circular:
- Demuestre que en el caso de movimiento curvilíneo (no circular) en el plano, la aceleración tiene componentes:
- Demuestre que
- Demuestre que en el caso general de movimiento curvilíneo, la aceleración tiene componentes:
- Demuestre que el movimiento circular con aceleración angular constante, tiene ecuaciones de movimiento:
- ¿Por qué el movimiento circular se puede considerar unidimensional?
- ¿Cómo se relacionan el periodo, la frecuencia y la velocidad angular?



Next: About this document ...
Willians Barreto
2007-11-02