Ecuación de Estado para una gas ideal

Con todos los datos experimentales acumulados sobre las propiedades macroscópicas de los gases (cuando consideramos bajas densidades) se ha encontrado el siguiente hecho sorprendente: para cualquier conjunto de variables termodinámicas, un gas ideal satisface en estado de equilibrio la siguiente ecuación de estado

$$\frac{pV}{NT}=k, \mbox{(forma molecular)}$$ (9)

donde

$$k=1,38\times 10^{-23} J K^{-1}$$

es la constante de Boltzman.

Si el número de moles se define como

$$n=\frac{N}{N_A},$$

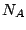donde $N_A$ es el número de Avogadro

$$N_A= 6,02 \times 10^{23} mol^{-1},$$

la ecuación de estado (9) la podemos escribir en términos de la constante universal de los gases

$$R=kN_A=8,31 J mol^{-1} K^{-1}$$

como

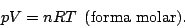$$pV=nRT \mbox{(forma molar).}$$ (10)

Decimos entonces que para bajas densidades los gases reales siguen la ecuación de estado (9) o equivalentemente (10). Además, enfatizamos que las propiedades macroscópicas observadas (y enunciadas como ``Leyes'' a través de (6), (7) y (8)) están contenidas en (9) o en (10).