INDICE

(1): Introducción

(2): Aproximación de una superficie de respuesta por polinomios:

(3-1): Requerimientos y propiedades deseables de los diseños óptimos:
(3-2): Estrategia experimental
(3-3): Método del ascenso más pronunciado:
(4): Diseños de primer orden:

(5-1): Diseños de segundo orden:
(5-2): Construcción de diseños compuestos centrales:
(6): Diseños Rotables:

(7): Análisis Canónico:

(8): Bibliografía:

(1): INTRODUCCION Regresar al Indice

Supóngase que la dependencia de una variable respuesta Y sobre los niveles x ₁, x ₂, ..., x _k

de k

variable cuantitativas o factores se puede expresar por el siguiente modelo matemático:

Y = f (x ₁, x ₂, ..., x _k) + e;e ~N( 0, s² ).

Esta relación funcional en general se llama una superficie de respuesta. Uno de los objetivos

más frecuente en una investigación por experimentación consiste en determinar los valores

de las k

variables independientes, x _i; (i = 1,...,k), l as cuales pueden producir un máximo

( o mínimo) de E(Y).

Se asumirá que en la mayoría de los casos prácticos, la forma de función f es desconocida
y aún cuando en un caso dado f puede ser muy complejo, siempre será posible aproximar la
función f satisfactoriamente por un polinomio en x _i; (i = 1,...,k); de algún grado adecuado
dentro de una región experimental previamente planificada.

A fin de estimar los parámetros de una función polinomial , que puede servir para aproximar
la superficie de respuesta f, necesitaremos emplear un diseño de experimento el cual se
puede denotar por : (x _1u, x _2u, ..., x _ku); u = 1,...,N; que constituye una selección de
N puntos en una región experimental de interés.

Después de realizar el experimento, utilizando el diseño indicado, se obtendrá la estimación
de la función f, que a su vez se puede someter a un análisis para averiguar acerca de las
condiciones que se deben imponer sobre las variables x₁, x₂, ..., x_k;para que E(Y) alcance
un valor óptimo, que podría ser un máximo o un mínimo, según sea el caso bajo estudio.

(2): Aproximación de una superficie de respuesta por polinomios:

Regresar al Indice

La aproximación de una relación funcional desconocida

, se puede hacer de la manera mas

simple por el modelo

lineal de primer orden:

Y = b₀ + b₁x ₁ + b₂x ₂+. . . + b_kx _k + e ; e~N( 0, s²).

el cual representa la ecuación de un plano.

En el caso de que el modelo de primer orden no sea adecuado, el siguiente modelo de segundo
orden se puede utilizar:

Y = b₀ + S b_ix _i + S b_iix _i²+ S b_ijx _ix _j + e ; (i,j =1, ..., k ; i < j); e~N( 0, s² ).

La superficie de respuesta del segundo orden dado por E(Y) puede ser una parábola, híperbola,
elipse o sus generalizaciones correspondientes en el caso k-dimensional. Así también en el
caso de que fuera necesario, superficies polinomiales de orden superior a dos, se pueden
utilizar. Una superficie polinomial de esta naturaleza, se debe considerar solo como una
aproximación de la verdadera relación funcional f en el interior de una región considerada en
el experimento. Una extrapolación que intenta hacer predicciones fuera de la región experimental
puede ser arriesgada y no confiable.

(3-1): Requerimientos y propiedades deseables de los diseños óptimos:

Regresar al Indice

Box y Hunter(1951) sugirieron las siguientes propiedades que deberían poseer los diseños multifactoriales de orden d:

(1): El diseño debe permitir la estimación de parámetros de una superficie de respuesta
polinomial con una precisión satisfactoria dentro de la región de interés.

(2): El número de puntos experimentales en el diseño no debe ser muy grande.

(3): El diseño debe posibilitar una verificación con exactitud, que el polinomio asumido
en el estudio es del grado adecuado.

(4): Debe permitir el uso de bloques cuando así sea conveniente.

(5): Debe formar un núcleo, del cual un diseño satisfactorio del grado d+1 se puede construir
en el caso de que se verifica que el grado d del polinomio no es adecuado.

(3-2): Estrategia experimental Regresar al Indice

En la selección de los puntos experimentales de un diseño, el investigador debe tomar en cuenta
las siguientes circunstancias que podrían influir su estrategía:

Magnitud del error experimental

Complejidad de la superficie de respuesta

Si o no es posible ejecutar el experimento en forma secuencial

(3-3): Método del ascenso más pronunciado: Regresar al Indice

Este método establece una regla que se utiliza en una serie de experimentos secuenciales para
pasar a una región de respuesta más alta en la búsqueda de una respuesta máxima.

Sea (0,0, ... ,0) el centro del primer experimento. Entonces esta regla de decisión determina las coordenadas del punto P = (x'₁, x'₂, ..., x'_k), el cual será el centro del próximo experimento.

Esta técnica consiste en seleccionar un diseño con pocos puntos experimentales y luego al
conducir el experimento, se obtienen las estimaciones de los parámetros correspondiente a un
modelo polinomial de grado uno.
Sea
Y_(estimado)= b_{0 +}b₁X₁ + b₂X₂ + .... +b_kX_k

la estimación de ecuación del plano en un experimento. Entonces el camino del ascenso mas pronunciado se toma al pasar al centro del próximo diseño a lo largo de los ejes :
X_1,X₂ ,..., X_ken cantidades proprcionales a : b₁ , b₂ , .... , b_krespectivamente.

(4) Diseños de primer orden: Regresar al Indice

Los diseños de primer orden son aquellos que permiten la estimación de parámetros de un
modelo polinomial de grado uno.
Ejemplos de diseños de primer orden:

Experimentos factoriales de la serie 2^k

Repitición fraccionada 1/2^pdel factorial 2^k

Estos diseños son muy convenientes en trabajos exploratorios para obtener el ajuste de una
relación lineal entre la respuesta como variable dependiente y las variables independientes.
Estos diseños también se pueden utilizar en las etapas iniciales de un programa de
experimentación secuencial en la búsqueda de la respuesta óptima.

Mas abajo, se presenta una lista de algunos diseños factoriales fraccionados que son útiles
como diseños de primer orden en las etapas priliminares en la exploración de una superficie
de respuesta.

Tabla 1: Algunos diseños útiles de primer orden formados por diseños factoriales 2^k-p

Número de factores

3
4
5
5
6

Tamaño del experimento

8
8
8
16
8

Fracción

1
1/2
1/4
1/2
1/8

G.L. por falta de ajuste

4
3
2
10
1

Propiedades: El diseño factorial fraccionado 1/2^ptiene las siguientes propiedades:

Existen 2^k-ppuntos experimentales.

de un total de 2^k-1efectos principales e interacciones correspondientes al experimento

factorial comple to, 2^p-1serán inseparable del parámetro b₀en el modelo y los restantes

2^k- 2^pefectos serán mutuamente inseparables en conjuntos de 2^p,siendo el número de

tales conjuntos igual a 2^k-p.

Mayores detalles de la construcción de los experimentos factoriales fraccionados se pueden
obtener en Raghava Rao (1971).
(5-1): Diseños de segundo orden: Regresar al Indice

Los diseños de segundo orden permiten la estimación de parámetros de un modelo polinomial
de grado dos. Ejemplos simples de este tipo de diseños son las series de 3^kfactorial. La
desventaja de la serie 3^kes que con k >3, el número de puntos experimentales que se requieren
para conducir el experimento, llega a ser muy alto. Además los parámetros b₁₁, ... ,b_kk; en
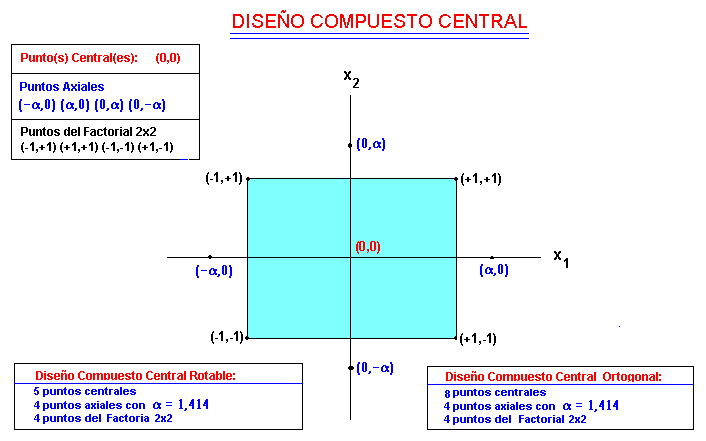
general se estiman con precisión relativamente baja. Box y Wilson (1951) han desarrollado una
familia de diseños llamados diseños compuestos que son mas convenientes para este propósito
y se presentan a continuación:

(5-2): Construcción de diseños compuestos centrales: Regresar al Indice

Construcción del diseño: Los puntos experimentales de este diseño consisten en:

(i): Puntos del factorial 2^ko su fracción, ampliado por :

(ii): 2k puntos axiales sobre los ejes de las variables independientes, denotados por:

(-a, 0, ... , 0); (a, 0, ... , 0); (0, -a, ... ,0); (0, a, ... ,0); ... ; (0, 0, ... , -a,); (0, 0, ... , a,)

(iii): Punto(s) sobre el centro del diseño.

El valor de a se puede elegir para :

(a): Dar la propiedad de ortogonalidad al diseño o

(b): Minimizar el sesgo que surge si el modelo planteado en una investigación es de grado

dos pero el modelo verdadero tiene grado superior a dos o

(c): Dar la propiedad de rotabilidad al diseño.

Uso de un diseño compuesto central en experimentación secuencial:

Los diseños compuestos centrales se pueden incorporar en un programa de experimentación secuencial. Este programa se puede iniciar con un factorial 2^kcon meta exploratoria y hará
posible obtener la estimación de un modelo de primer grado. Si en esta etapa, mediante el uso
de F.V. de falta de ajuste, se verifica que el modelo cuadrático debería ser el más apropiado,
entonces se procederá a agregar (2k+1) puntos adicionales, el cual lo convierte en un diseño
compuesto central. En la segunda etapa se utilizan (2^k+2k +1) puntos expeimentales en el análisis estadístico y se estiman los parámetros de grado dos.
Construcción de un diseño compuesto central ortogonal:

Box y Wilson(1951) han demostrado que para dar la propiedad de ortogonalidad al diseño, se
elige el valor de a tal que:

a = (mF/4) ^1/4, donde m = ((F+T) ^1/4- F^1/2)²

en que F = número de puntos de 2^kcompleto o su fracción apropiada y T = número de puntos adicionales para construir un diseño compuesto central.
cuando a = 1.215, este diseño se llama un diseño compuesto ortogonal.

(6): Diseños Rotables: Regresar al Indice

En consideración del problema de selección de diseños óptimos, Box y Hunter (1951),
propusieron el criterio de rotabilidad de un diseño.

Definición del concepto de rotabilidad de un diseño:

Sea (0, 0, ... , 0) el centro de un diseño. Sea:

Y_(est.)(u)= b₀ + S b_ix _iu + S b_iix _iu²+ S b_ijx _iux _ju ; (i,j =1, ..., k ; i < j); (u = 1, ... , N);

la respuesta estimada en el punto (x _1u, x _2u, ..., x _ku); Sea:
Var.(Y_(est.)(u)) =(a'(X' X)^-1a)s² , donde
a' = (1, x _1u , ... , x _ku; x ²_1u, ... , x² _ku; x _1u x _2u, ... , x _k-1, _u x _ku;)

Un diseño se llama rotable si y solo si Var.(Y_(est.)(u)) es invariante para todos los puntos que
sean equidistante desde el centro del diseño.

Nota : Si un diseño es rotable, entonces Var.(Y_(est.)(u)) será una función solamente de
x ²_1u+ x ²_2u+ ^{, ... ,} + x ²_ku
Construcción de un diseño Compuesto central rotable:

Los puntos experimentales de este diseño consisten en:

(i): n_cpuntos del factorial 2^ko su fracción apropiada , denotados por : (±1, ±1 , ... , ±1)

(ii): n_a puntos axiales sobre los ejes de las variables independientes, denotados por:

(±a, 0, ... , 0); (0, ±a, ... ,0); ... ; (0, 0, ... , ±a); donde a = (F)^1/4 , en que F es igual al
número de puntos experimentales del factorial 2^ko su fracción apropiada.

(iii): n_opunto(s) sobre el centro del diseño. (0, 0, ... , 0);

Sea l₄= N/( n_c+ 4(1 + (n_c)^1/2)), el parámetro del diseño rotable. La selección del valor
de l₄fija el número de puntos centrales de un diseño. Los valore de l₄recomendados por
Box y Wilson se presentan en la tabla a continuación:
Tabla 2: Valores de l₄recomendados por Box y Wilson

_k l₄

2
3
4
5
6
7
8

0,7844
0,8385
0,8704
0,8918
0,9070
0,9184
0,9274

(7): Análisis Canónico: (7-1): Ejemplo1: Khuri y Cornell, Página 170

                                                    1

                   OBS      Y      OTEMP    OTIEMPO      TEMP       TIEMPO

                     1    93.6    125.90     171.9     -1.00000    -1.00000
                     2    91.7    125.90     218.1     -1.00000     1.00000
                     3    92.5    145.90     171.9      1.00000    -1.00000
                     4    92.9    145.90     218.1      1.00000     1.00000
                     5    96.2    135.90     195.0      0.00000     0.00000
                     6    97.0    135.90     195.0      0.00000     0.00000
                     7    92.7    121.75     195.0     -1.41421     0.00000
                     8    92.8    150.04     195.0      1.41421     0.00000
                     9    93.4    135.90     162.3      0.00000    -1.41421
                    10    92.7    135.90     227.7      0.00000     1.41421
                                                                                              

                       


                         Response Surface for Variable Y: RENDIMIENTO

                               Response Mean           93.550000
                               Root MSE                 0.336892
                               R-Square                   0.9825
                               Coef. of Variation         0.3601




                           Degrees
                              of       Type I Sum
          Regression       Freedom     of Squares     R-Square    F-Ratio    Prob > F

          Linear                 2        0.782267      0.0302      3.446     0.1349
          Quadratic              2       23.346250      0.9012      102.9     0.0004
          Crossproduct           1        1.322500      0.0511     11.652     0.0269
          Total Regress          5       25.451016      0.9825     44.849     0.0013




                         Degrees
                            of         Sum of
        Residual         Freedom       Squares       Mean Square    F-Ratio    Prob > F

        Lack of Fit            3        0.133984        0.044661      0.140     0.9247
        Pure Error             1        0.320000        0.320000
        Total Error            4        0.453984        0.113496



                                                                                    
                    Degrees                                                         
                      of       Parameter     Standard     T for H0:                
 Parameter          Freedom    Estimate        Error     Parameter=0  Prob > |T|    

 INTERCEPT             1        96.600000      0.238218      405.5      0.0000       
 TEMP                  1         0.030178      0.119109      0.253      0.8125       
 TIEMPO                1        -0.311244      0.119109     -2.613      0.0592       
 TEMP*TEMP             1        -1.981250      0.157567    -12.574      0.0002       
 TIEMPO*TEMP           1         0.575000      0.168446      3.414      0.0269        
 TIEMPO*TIEMPO         1        -1.831250      0.157567    -11.622      0.0003       




             Degrees
                of       Sum of
  Factor     Freedom     Squares     Mean Square  F-Ratio  Prob > F

  TEMP           3       19.274250      6.424750   56.608   0.0010   TEMPERATURA (CENTIGRADO)
  TIEMPO         3       17.427660      5.809220   51.184   0.0012   TIEMPO (SEGUNDOS)

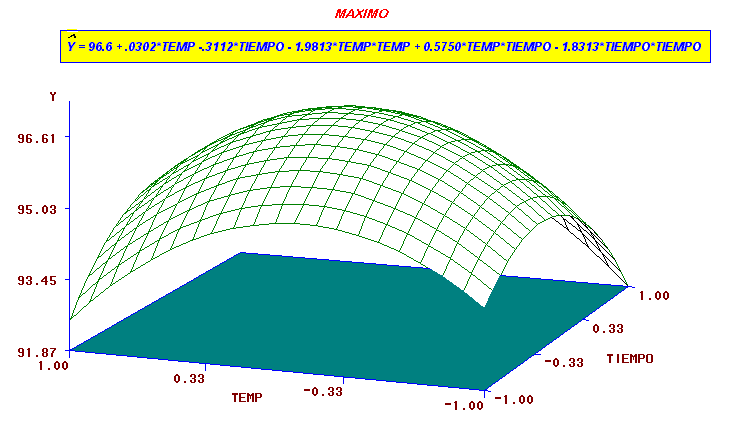
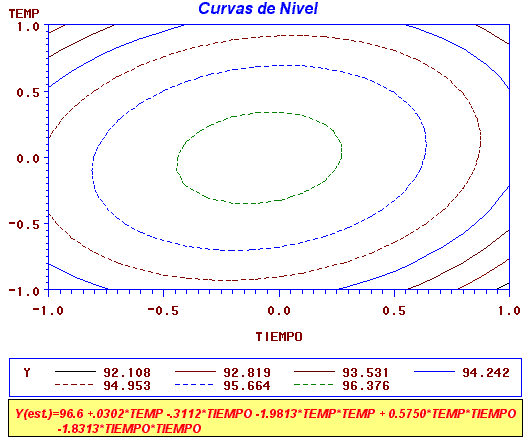
                             Ejemplo: Khuri y Cornell, Página 170                             4

                            Canonical Analysis of Response Surface
                                     (based on coded data)

                                 Critical Value
             Factor           Coded          Uncoded

             TEMP            -0.003412       -0.004826    TEMPERATURA (CENTIGRADO)
             TIEMPO          -0.060627       -0.085739    TIEMPO (SEGUNDOS)


                       Predicted value at stationary point     96.613270


                                                 Eigenvectors
                          Eigenvalues        TEMP           TIEMPO

                            -3.218257        0.611383        0.791335
                            -4.406743        0.791335       -0.611383


                                Stationary point is a maximum.

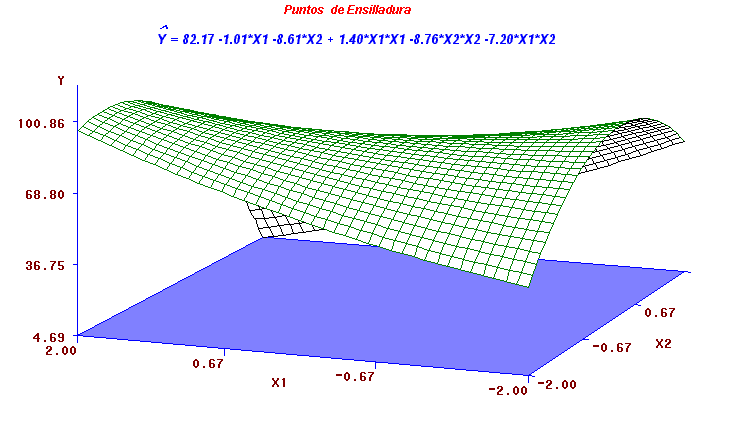
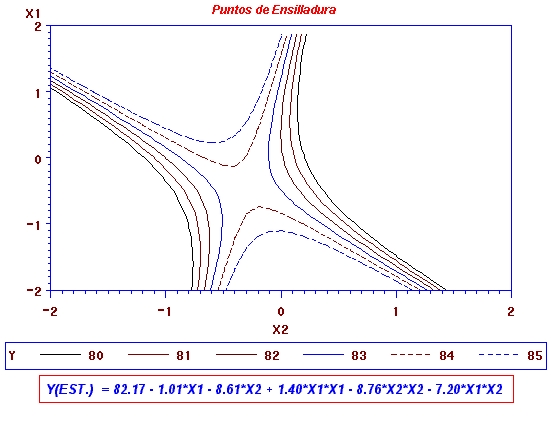
(7-2): Ejemplo 2: Puntos de Ensilladura

Bibliografía: Regresar al Indice

(1): Box, G.E. P. y J.S. Hunter (1951): Multifactor experimental designs for exploring response
surfaces. J.R.S.S. ser. B, vol. 13, No. 1, 195-240.

(2): Box, G.E. P. y K.B. Wilson (1951): On experimental attainment of optimum conditions.
J.R.S.S. ser. B, vol 13, No. 1 -45.

(3): Cornell, John A:(1990.): How to apply response surface methodology. Milwaukee, WI .

(4): Khuri, André I. y John A. Cornell.(1996): Response surfaces : designs and analyses .
Marcel Dekker, New York .

(5): Myers, Raymond H. y Douglas C. Montgomery.(1995.): Response surface methodology :
process and product optimization using designed experiments. Wiley, New York.

(6): Raghava Rao, D. (1971): Construction and combinatorial problems in Design of Experiments.
Wiley, New York.

(7): S.P.Sinha: Comparación de precisión y sesgo de algunos Diseños Experimentales de
superficie de respuesta. Publicación 80-01, I.E.A.C., U.L.A. 1980.

Regresar al Menú Principal