MATEMÁTICAS DISCRETAS

PROFESOR:  JACINTO D'AVILA

REALIZADO POR: NARSI RODRÍGUEZ

EMAIL: narsirodri@hotmail.com

    PREGUNTA No: 37

Notación y terminología:

    Este problema es está planteado completamente en Español. Cuando se dice que "cualquier par de ellas se interceptan" significan para mayor precisión todas estas rectas tendrán que cortarse entre si pero sin tener ningún punto en común.

Antecedentes:   

    Este problema y otros parecidos donde se utiliza la recurrencia pueden conseguirse en el libro "El Arte de Contar" de José Rodriguez.

PREGUNTA 37.

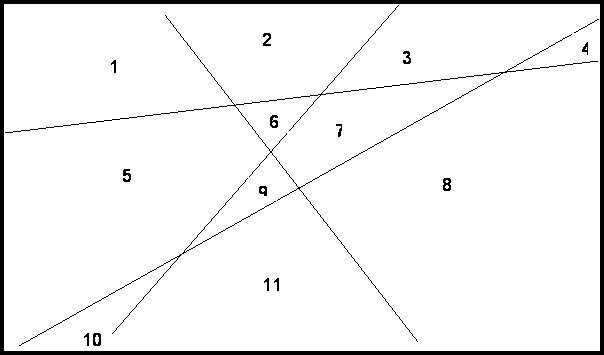
    Suponga que dibujamos n líneas rectas sobre un pedazo de papel, de modo que cualquier par de ellas se interceptan y además nunca tres líneas tienen un punto en común. ¿En cuantas regiones dividen estas n líneas al plano?

RESPUESTA 37.

    Al Dividir una hoja de papel con una línea la partimos en 2 espacios, cuando hay dos (2) líneas dividimos en 4 espacios así sucesivamente, en el ejemplo grafico mostraremos 4 líneas que se cortan todas entre si y no tienen puntos en comunes.

    Para este ejercicio utilizaremos las relaciones recurrentes ya  que esta es una técnica de contaje que nos permite resolver problemas de enumeración, determinando las respuestas, sucesivamente, para valores cada vez mayores de n.

Este ejercicio se resume en una formula abierta como:

L₁ = 2

L₂ = 2 + 2 = 4

L₃ =  4 + 3 = 7

L₄ = 7 + 4 = 11

.

.

.

                                         donde n = 1, 2, 3, 4, ......

    También se pudo Obtener un a Formula Cerrada la cual es:

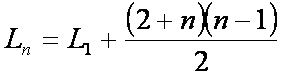
    Moraleja: Las funciones recurrentes pueden ser muy útil para las generalizaciones de diversos problemas en la vida real, es una manera de ir de lo abstracto a lo sencillo, con una formula.