Matemáticas Discretas

Problema de Función Generatriz

Realizado por : Luis Gerardo Peña Camacho

C.I. 13.966.504

mail to: luispc@intercable.net.ve

12) Considere la sucesión (a_i) = (1, 5, 19, 65, 211,.........) que cumple con la relación recurrente:

a_n = 5a_n-1 – 6a_n+2

Encentre la Función Generatriz para (a_i).

Solución:

Tenemos que:

a₀ = 1 = F₀;

a₁ = 5 = F₁;

a₂ = 19 = F₂;

a₃ = 65 = F₃;

a₄ = 211 = F₄;

a₅ = 665 = F₅;

Sabemos que:

F(z) = F₀ + F₁ z + F₂ z² + F₃ z³ + F₄ z⁴ +.................... + F_n zⁿ = F_n zⁿ

La serie que define a la función F(z) tiene una propiedad interesante que se observa al multiplicar por -5z y por 6z²

(a) F(z) = F₀ + F₁ z + F₂ z² + F₃ z³ + F₄ z⁴ + F₅ z⁵ + F₆ z⁶ + F₇ z⁷.............

(b) -5z F(z) = - 5F₀ z - 5F₁ z² - 5F₂ z³ - 5F₃ z⁴ - 5F₄ z⁵ - 5F₅ z⁶ - 5F₆ z⁷..........

(c) 6z² F(z) = 6F₀ z² + 6F₁ z³ + 6F₂ z⁴ + 6F₃ z⁵ + 6F₄ z⁶ + 6F₅ z⁷...............

Sumando (a), (b) y (c) tenemos

F(z) (1 -5z + 6z²) = F₀ + (F₁ - 5F₀)z + (F₂ -5F₁ + 6F₀)z² + (F₃ -5F₂ + 6F₁)z³.............

Sustituyendo los valores de la sucesión tenemos:

F(z) (1 -5z + 6z²) = 1 + (5 -5)z + (19 - 5*5 + 6*1)z² + (65 - 5*19 + 6*5)z³.........

F(z)(1 -5z + 6z²) = 1 + (0)z + (0)z² + (0)z³ + (0)z⁴ + (0)z⁵...................

Por tanto

F(z) = que representa la Función Generatriz de (a_i)

Podemos encontrar una formula cerrada de (a_i) a partir de la Función Generatriz descomponiéndola en fracciones Parciales, tenemos:

F(z) =. =

Resolviendo a y b tenemos que a = 6 y b = - 6, sustituyendo tenemos:

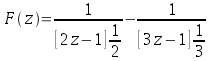
Multiplicando por (-1) tenemos:

si a = 3 y b = 2 tenemos:

Sabemos que:

Sustituyendo en F(z) queda:

En tal sentido la forma cerrada de (a_i) viene dada por:

Por tanto la Sucesión: a_n = 5a_n-1 -6a_n+2

posee la función generatriz: F(z) =.

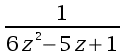y la formula cerrada de la recurrencia: