Matemáticas Discretas
|
|
|
|
Notación y Terminología:
Antes de mostrar la solución del ejercicio, se les mostrara una definición
sobre la base del problema y quien fue el creador de la famosa sucesión de
Fibonacci.
-
Sucesión de Fibonacci: en matemáticas,
sucesión de números en la que cada término es igual a la suma de los dos
términos precedentes: 0, 1, 1, 2, 3, 5, 8, 13, 21, y así sucesivamente. Esta
sucesión fue descubierta por el matemático italiano Leonardo Fibonacci. Los
números de Fibonacci tienen interesantes propiedades y se utilizan mucho en
matemáticas. Las estructuras naturales, como el crecimiento de hojas en
espiral en algunos árboles, presentan con frecuencia la forma de la sucesión
de Fibonacci.
Leonardo Fibonacci (c. 1170-c. 1240), también llamado Leonardo Pisano,
matemático italiano que recopiló y divulgó el conocimiento matemático de
clásicos grecorromanos, árabes e indios y realizó aportaciones en los
campos matemáticos del álgebra y la teoría de números; introdujo los
números arábigos en Europa. Nos han quedado pocas obras de Fibonacci.
Escribió sobre la teoría de números, problemas prácticos de matemáticas
comerciales y geodesia, problemas avanzados de álgebra y matemáticas
recreativas. Sus escritos sobre matemáticas recreativas, que a menudo los
exponía como relatos, se convirtieron en retos mentales clásicos ya en el
siglo XIII. Estos problemas entrañaban la suma de sucesiones, como la
sucesión de Fibonacci que él descubrió (kn = kn-1 +
kn-2, por ejemplo, 1, 2, 3, 5, 8, 13…). A cada término de esta
sucesión se le denomina número de Fibonacci (la suma de los dos números
que le preceden en la sucesión).
Antecedentes:
Aparece en el libro del profesor José Rodríguez, El Arte de Contar. Universidad de Los Andes.
- Ejercicio 25.-
Demuestre que:
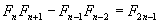
Para resolver este ejercicio primero se deben conocer algunas propiedades o formulas equivalentes que nos ayudara a comprender más fácilmente los problemas que se nos plantean.
La formula base o general de Fibonacci es:
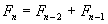
A partir de aquí se pueden obtener otras formulas equivalentes pero como se dijo anteriormente las formulas a continuación harán el fácil entendimiento de lo planteado:
La demostración es la siguiente:
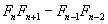por propiedades de Fibonacci podemos usar las formulas equivalentes y de esta manera podemos desglosar 
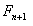y 
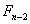respectivamente y la formula resulte 
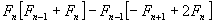, realizamos la multiplicaciones respectivas y el resultado es: 
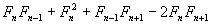, como se observa hay elementos similares por lo tanto se suma algebraicamente quedando 
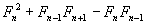, agrupamos ahora términos semejantes 
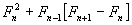y por propiedades de Fibonacci sabemos que 
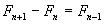, y lo sustituimos en la ecuación 
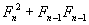y de esta manera resultando al final 
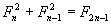y se llego a ello gracias al uso de las propiedades antes escritas anteriormente y de esta manera demostrar lo que se nos pidió.
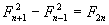
Demostración: (de igual manera las propiedades de Fibonacci se harán uso en el problema)
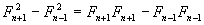, se desglosara las formulas 
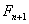y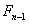 
respectivamente
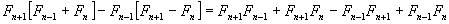, se realizan multiplicaciones y sumas algebraicas respectivamente resultando
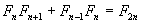por las propiedades de Fibonacci.
Moraleja: Muchas
de las teorías matemáticas más abstractas tienen un
profundo sentido práctico.
 escríbeme si necesitas aclarar alguna duda o comentario al respecto |
|
 |
|
|
