PROBLEMA 11

 

Notación y Terminología

En los siguientes tres ejercicios se resolverán funciones generatrices ordinarias para encontrar las sucesiones (  ), las cuales se representan por una serie de potencias, por ejemplo:

 

 

Antecedentes: Problemas similares, pero no idénticos, aparecen en el libro del profesor José Rodríguez, El Arte de Contar, Capítulo III, Parte 1. Función Generatriz. Página 89. Ejemplo 1.6 y 1.7. Universidad de Los Andes.

 

PREGUNTA 1.1

Encuentre la sucesión  asociada a la función generatriz:

 

 

RESPUESTA 1.1

Factorizando la expresión anterior obtenemos lo siguiente:

 

 

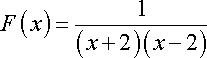
Haciendo una simplificación de la expresión anterior, podemos decir:

 

 

 

De donde obtenemos que:

 

 

 

 

De lo anterior obtenemos

 

 

 

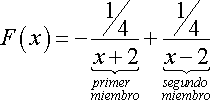
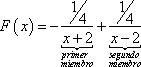
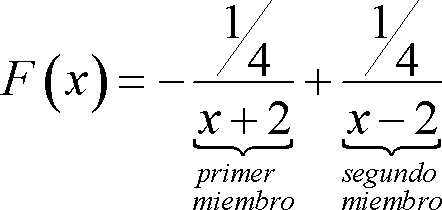
Resolvemos el Primer Miembro de la ecuación anterior y proponemos el cambio de variable  

 

 

 

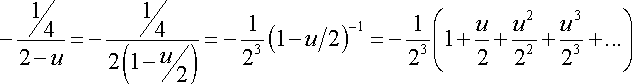
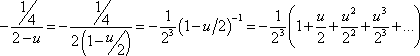
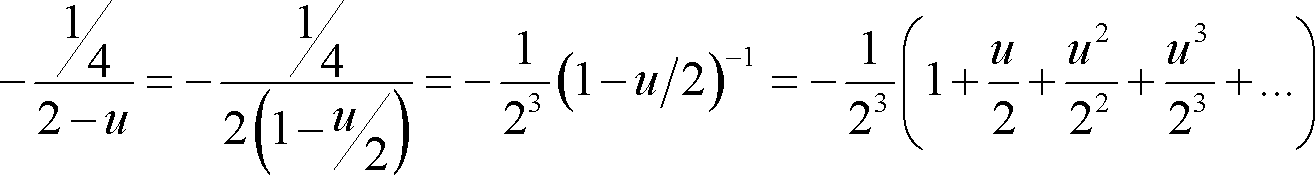
Devolviendo el cambio de variable planteado anteriormente obtenemos

 

 

 

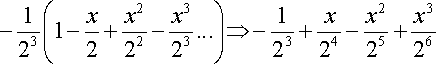
Resumiendo

 

 para  

 

Resolviendo el Segundo Miembro de la ecuación, tenemos:

 

 

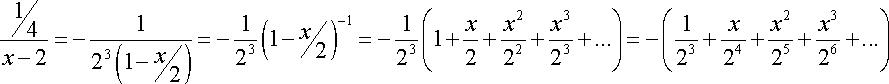
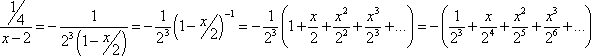
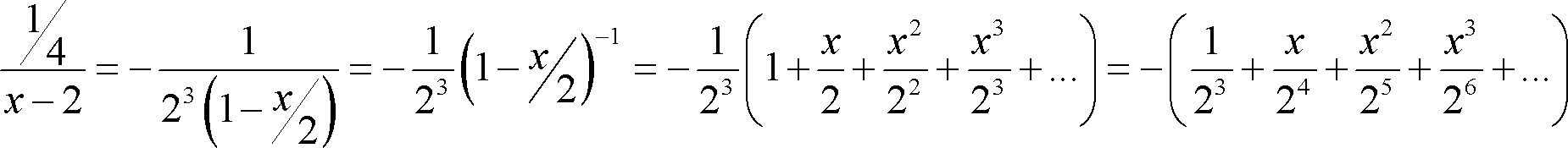
Resumiendo

 

 para  

 

La respuesta a este problema se encuentra al sumar los términos encontrados en la solución del Primer Miembro y el Segundo Miembro

 

 para  

 

PREGUNTA 1.2

Encuentre la sucesión  asociada a la función generatriz:

 

RESPUESTA 1.2

 

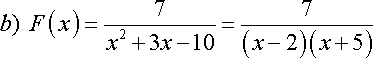
Haciendo una simplificación de la expresión anterior, podemos decir:

 

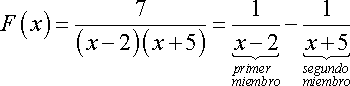
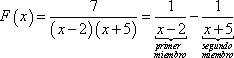
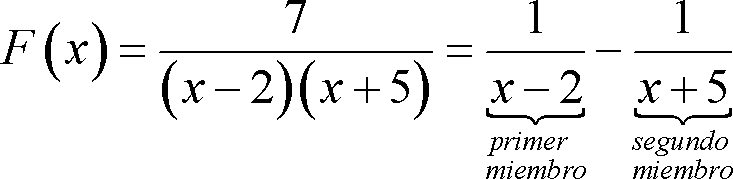
Resolviendo el primer miembro de la ecuación anterior, tenemos que:

 

 

 

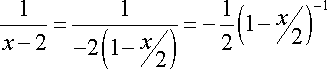
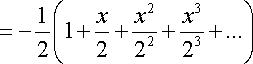
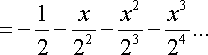
Por lo tanto, para el primer miembro de la ecuación encontramos  para  

Resolviendo el segundo miembro de la ecuación, tenemos que:

 

Aplicamos un cambio de variable

 

Ahora, encontramos que:

 

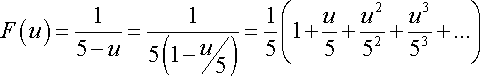
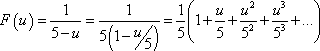
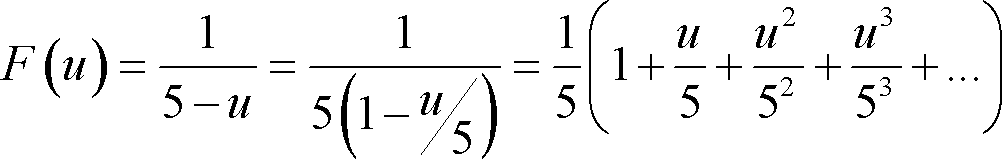
Devolviendo el cambio hecho anteriormente

 

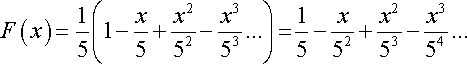
Por lo tanto, para el segundo miembro de la ecuación encontramos 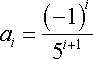 para  

Restando el primer miembro menos el segundo miembro de la ecuación, obtenemos que:

 para  

 

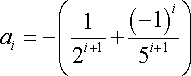
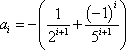
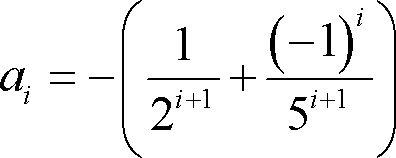
PREGUNTA 1.3

Encuentre la sucesión  asociada a la función generatriz:

 

RESPUESTA 1.3

 

 

 

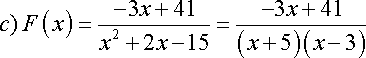
Haciendo una simplificación de la expresión anterior, podemos decir:

 

 

 

Si  

Si  

 

Con lo anterior, podemos deducir lo siguiente

 

 

 

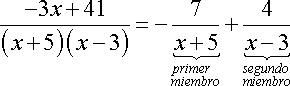
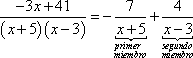
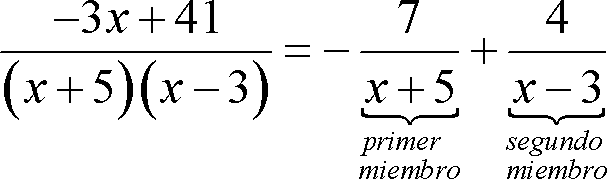
Resolviendo el primer miembro de la ecuación anterior

 

 

Se propone el cambio de variable , por lo que nos queda

 

 

 

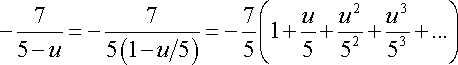
Devolviendo el cambio propuesto anteriormente, tenemos que

 

 

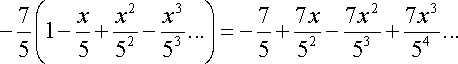
Con lo anterior podemos decir que  para  

 

Resolviendo el segundo miembro de la ecuación, tenemos

 

 

 

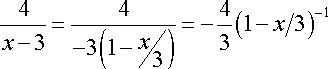
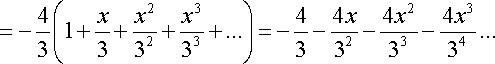
De esta manera obtenemos  para  

Sumando los resultados del primer y segundo miembro de la ecuación, se obtiene lo siguiente:

 para  

 

Moraleja

Las funciones generatrices nos permiten crear expresiones “cerradas”, para ello no es necesario conocer el término , es más, podemos partir de la expansión de la expresión “cerrada” para encontrar el número combinatorio . La comodidad que nos ofrece la función generatriz se basa en el hecho de que no es necesario recurrir a la expansión de las expresiones “cerradas” para conocer los distintos coeficientes  que acompañan a las variables  en dicha expansión.

 

Producido por: Milton Mazzarri