Guía de Estudios de Matemática Discreta – Parcial 4.

Producida por

Johana C. Zambrano G. <tiajoha17@hotmail.com>

PROBLEMA 1

Notación y terminología: Para los problemas presentados a continuación se hará uso del concepto de función generatriz la cual es una sucesión (a_i) que se representa por una serie de potencias. También es útil conocer las series geométricas, como por ejemplo: la serie del binomio; así como el triángulo de Pascal, los números de Stirling y las particiones de un entero.

F(x)= a₀ + a₁x +a₂x²+a₃x³+.....................

1/(1-x)ⁿ=1+x +x²+x³+............

Antecedentes: Ejemplos de ilustración acerca de funciones generatrices se encuentran en el libro del profesor José Rodríguez, El Arte de Contar, Capítulo 3. Universidad de Los Andes. Acerca de las particiones de un entero revisar capítulo 1 parte 6 (fórmula y tabla. Sugerencia: completar la tabla que allí se encuentra). Los números de Stirling y triángulo de Pascal revisar la copia facilitada por el profesor Jacinto Dávila.

PREGUNTA 1.a

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.a

Desarrollando los productos con previa visión de los factores que están, podemos realizar las multiplicaciones de una forma inteligente de tal manera que se nos eliminen la mayor cantidad de términos y así realizar menos productos. En éste caso vemos que al multiplicar el primer y tercer factor se nos eliminan los términos cuadráticos.

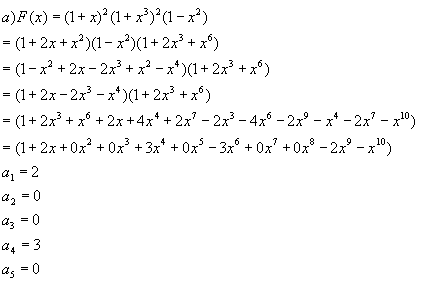
Usando la fórmula de la función generatriz obtenemos los coeficientes de la sucesión que nos piden. Vemos que el polinomio hasta el factor de grado 5 tiene los coeficientes positivos y a partir de ahí se repiten los mismos términos de manera decreciente a la forma que obtuvimos en los primeros 5 pero con signo negativo.

PREGUNTA 1.b

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.b

En ésta ocasión como no tenemos factores negativos no podemos eliminar términos . Desarrollando el factor cuadrático obtenemos los siguientes términos :

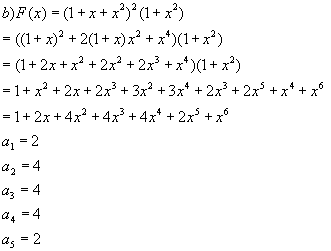
Al llegar a la solución, el polinomio que se obtuvo es simétrico. Para hallar una relación que involucre los términos a_k podemos utilizar :

a_i =Pm(n) (La cual significa el número de particiones de n en m que nos representa éstos términos)

para i=1,2,3 donde m=5-i y n=5+i. Y los restantes términos son a₄ =a₃ y a₅=a₁

PREGUNTA 1.c

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.c

Nuevamente resolviendo los productos entre los factores:

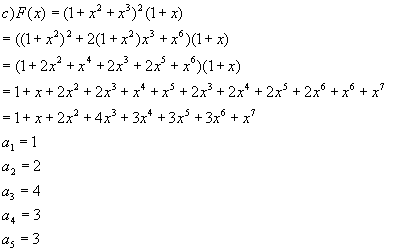
Volvemos a comparar los términos y utilizaremos particiones para identificar lo que cuentan éstos.

a_i =Pm(n) para i=1,2,3 donde m=6-i y n=4+i y a₄ =a₅ si i=4 entonces m=i-1 y n=i+2

PREGUNTA 1.d

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.d

Resolviendo los productos:

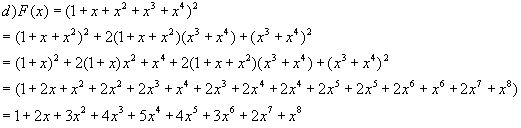
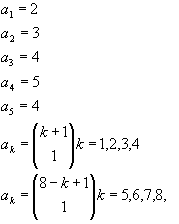
En éste caso los términos a_i representan combinatoria las cuáles se les pudo conseguir una fórmula general para representarlos. El polinomio obtenido es simétrico.

PREGUNTA 1.e

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.e

Realizando las operaciones:

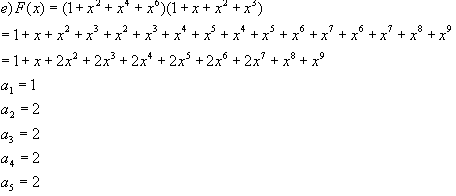
Para los a_i volvemos a utilizar particiones. a_i =Pi(n) para i=1,2,3 ,4,5 donde n=2+i. El polinomio es simétrico.

PREGUNTA 1.f

Encuentre F(x)|_xi para i=1,2,3,4 y 5 en :

RESPUESTA 1.f

Para no desarrollar el producto completo y ahorrar trabajo usamos la fórmula del binomio:

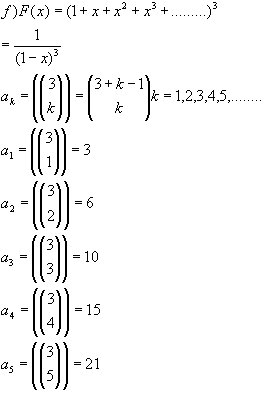
Los a_k representan el número de combinaciones con repetición de 3 elementos tomados de a k. También podemos notar que a diferencia de las otros resultados, ésta no es simétrica y cada coeficiente representa la suma de los primeros k+1 números por ejemplo cuando k=2 es el resultado de la suma de 1+2+3=6.

Como también se representan con los números de Stirling y la combinatoria de la siguiente manera:

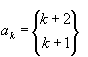
k+2 subconjunto k+1

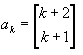
k+2 ciclo k+1

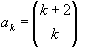
Combinatoria de k+2 en k

Donde k=1,2,3,4.................

Moraleja: Es conveniente chequear (observar) con detenimiento los factores y productos que se tienen para evitar cálculos tediosos.