Guía de Estudios de Matemáticas Discretas – Parcial 4.

Producida por

María Laura Sarmiento <marialaurasc@gmail.com>

Prof. Jacinto Dávila

Semestre A-2004

Capítulo: Función Generatriz

Página 114

El Arte de Contar

Profesor José Rodríguez

PROBLEMA 6

Notación y terminología: La solución del problema consiste en hallar una función del tipo polinomio, cuyos coeficientes permitan determinar de una manera directa el número de formas de sacar objetos de una pila, es decir, el exponente de la x corresponde al total de objetos a extraer, y el respectivo coeficiente indica la respuesta. Llamaremos a este polinomio: Función Generatriz para (a_i), donde a_i es el número de maneras de seleccionar i objetos de una pila.

Antecedentes: este problema es equivalente a hallar las soluciones no negativas de la ecuación:

Previamente hemos estudiado este resultado como:

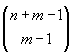
De igual manera es necesario recordar un resultado obtenido, producto de la expansión del Binomiocomo el siguiente:

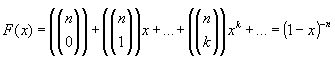
Donde es el número de combinaciones con repetición y está expresado como:

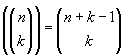
PREGUNTA 6.1

Encuentre una función generatriz para (a_i), donde a_i es el número de maneras de seleccionar i objetos de una pila de 10 medios, 7 reales, 9 centavos y 12 bolívares.

RESPUESTA 6.1

Este problema corresponde a buscar las soluciones no negativas de la ecuación:

con la condición de que:

Donde:

X₁ = número de medios que podemos elegir.

X₂ = número de reales que podemos elegir.

X₃ = número de centavos que podemos elegir.

X₄ = número de bolívares que podemos elegir.

Ahora construimos un polinomio asociado a cada tipo de moneda y luego multiplicamos estos polinomios, de modo tal que el producto contenga términos con exponentes entre 0 y el número de monedas de cada tipo.

El número de estos productos para los cuales los exponentes suman i es la solución de la ecuación. Es necesario aclara que ya no trabajaremos con las 4 variables anteriores si una sola usada en los polinomios.

Antes de seguir con la solución del problema, veamos que indican estos polinomios y a que solución nos llevan. Para estos utilicemos un pequeño ejemplo que consista en sacar i elementos de una caja que contiene una bola roja y una negra. Aplicando el procedimiento anterior, la solución del problema corresponde al conjunto de soluciones no negativas de la ecuación respectiva y posteriormente determinamos los polinomios:

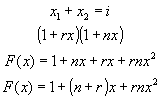
Claramente se puede observar que el producto de estos polinomios representa la función generatriz buscado y si colocamos las letras de elemento respectivo, cada coeficiente indica dos cosas:

• El número de elementos en la suma que acompaña a cada término es el número de formas de sacar i objetos de la caja donde i es el exponente de la x que acompaña a dicho término.

• Cada miembro de la suma muestra cual es la combinación posible.

Si estudiamos el polinomio que se obtuvo anteriormente, nos damos cuenta de que hay una sola forma de sacar 0 objetos (esto es i=0), 2 formas de sacar un objeto (n+r) y esto indica que puede ser la bola roja o la blanca (i=1) y 1 forma de sacar 2 objetos, esto es sacar la bola roja y la negra al mismo tiempo (i=2).

Ahora volvemos al problema original, una vez determinados los polinomios asociados observemos lo siguiente:

Si i=0, no se escoge ninguna moneda la única posibilidad es:

Luego .

Si i =1, se escoge una sola moneda de manera que las posibilidades son:

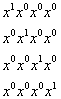
Total 4 posibilidades. Luego .

Si i = 2, se escogen dos monedas. Las posibilidades son:

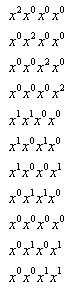
Total 10 posibilidades. Luego .

No es necesario hacer la búsqueda de soluciones de esta forma pero en este primer caso se realiza con el fin de explicar mejor el procedimiento.

La función generatriz será entonces el producto de los polinomios:

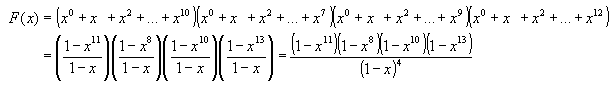
Una vez obtenida, sabemos que el número de formas de sacar i objetos viene determinado por el coeficiente del término con xⁱ que resulta del producto de los polinomios pero que ha quedado expresado como de una manera reducida.

Sin embargo en este primer problema y para aclarar aún más el concepto, realizamos el producto quedando lo siguiente:

Considerando lo antes mencionado tenemos:

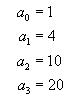
Donde a₀ representa el número de formas de sacar 0 monedas de la pila, a₁ representa el número de formas de sacar 1 moneda de la pila y esto se puede generalizar a:

PREGUNTA 6.2

Encuentre una función generatriz para (a_i), donde a_i es el número de maneras de seleccionar i objetos de una pila de 4 pantalones azules, 5 blancos y de ILIMITADOS pantalones rojos.

RESPUESTA 6.2

Este problema se resuelve de la misma forma que el problema anterior, con la única diferencia de que la cantidad de uno de los tipos de objetos es ilimitada, en este caso el polinomio asociado no tendría un límite, pero esto es perfectamente válido ya que podemos expresarlo en términos de la serie geométrica como se mostrará a continuación:

La solución del problema viene dada por el número de soluciones no negativas de la ecuación:

con la condición de que:

Donde:

X₁ = número de pantalones azules que podemos elegir.

X₂ = número de pantalones blancos que podemos elegir.

X₃ = número de pantalones rojos que podemos elegir.

Construimos ahora los polinomios asociados:

Recordemos que:

es la serie geométrica.

Ahora hallamos la función generatriz:

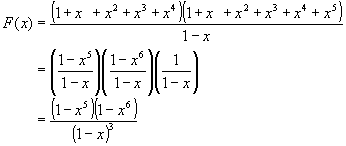
De igual forma hallamos el polinomio asociado a este producto para determinar algunos de los valores que buscamos e interpretar la solución.

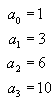
Así mismo, generalizando:

PREGUNTA 6.3

Encuentre una función generatriz para (a_i), donde a_i es el número de maneras de seleccionar i objetos de una pila de ILIMITADAS cantidades de naranjas, mangos, tomates, guayabas y uvas.

RESPUESTA 6.3

Una vez más utilizamos el mismo procedimiento para obtener la solución, que viene dada por el número de soluciones no negativas de la ecuación:

con la condición de que:

Donde:

X₁ = número de naranjas que podemos elegir.

X₂ = número de mangos blancos que podemos elegir.

X₃ = número de tomates rojos que podemos elegir.

X₄ = número de guayabas rojos que podemos elegir.

X₅ = número de uvas rojos que podemos elegir.

De nuevo construimos los polinomios asociados:

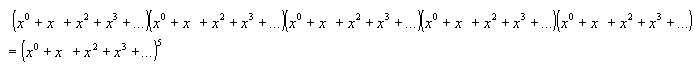
y recordando que:

es la serie geométrica, ahora hallamos la función generatriz:

Ahora recordando el resultado producto de la expansión del binomio:

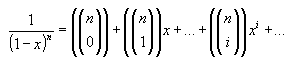
podemos darle el valor de n = 5, para obtener de nuevo la función objetivo y ver rápidamente los coeficientes que buscamos.

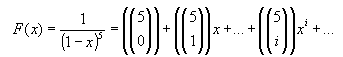
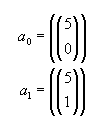
Así, entonces de manera generalizada tenemos:

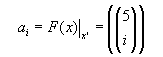
donde,

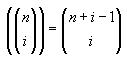
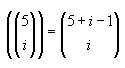
Moraleja: el método de los polinomios asociados para determinar una función generatriz es de gran utilidad, de una manera práctica y sencilla obtuvimos un polinomio cuyos coeficientes nos daban el resultado deseado (función generatriz). Además, el resultado producto de la expansión del binomio es muy útil, puesto que buscando la manera de expresar los polinomios de forma reducida, siempre llegamos a formas que involucran a la serie geométrica.