:
cardinalidad de la colección que contiene los
k-submulticonjuntos de un multiconjunto S = { x1∞,
..., xn∞}Matemáticas Discretas. Problema No. 8
Guía de Estudios de Matemáticas Discretas – Problema 8.
Producida por
Marco Camejo
<m_camejo@yahoo.com
PROBLEMA 8
Notación y terminología: Las k-combinaciones de un conjunto de n elementos, son todas las maneras de escoger elementos del conjunto, tomando k a la vez.
:
cardinalidad de la colección que contiene los
k-submulticonjuntos de un multiconjunto S = { x1∞,
..., xn∞}
Antecedentes: Los k-submulticonjuntos de S = { x1∞, ..., xn∞} suelen denominarse las k-combinaciones con repetición del conjunto S = { x1, ..., xn}.
PREGUNTA 8.
Encuentre una función generatriz para el número de k-combinaciones de S = { x1, ..., xn}, donde x1 aparezca un número impar de veces, x2 un número par de veces y los restantes cualquier número de veces.
RESPUESTA 8.
La función generatriz
para la sucesión en donde a puede aparecer cualquier
número de veces
es:
De manera similar, la función generatriz para la sucesión en la cual a aparece un numero impar de veces es:
Y la función generatriz para la sucesión en la cual a aparece un número par de veces es:
En cada una de estas tres funciones generatrices, hacemos a=1, para obtener que el termino que acompaña a x a la k-ésima potencia, es la k-combinación buscada en cada caso. Las funciones serán entonces:
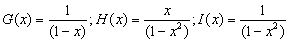
Se busca que x1 aparezca un número impar de veces y x2 un numero par de veces, para los restantes n-2 términos no hay restricción, entonces la función generatriz para la expresión completa sería:
Finalmente, el coeficiente que acompaña a x elevada a la k-esima potencia, es el número que estamos buscando:
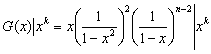
Moraleja: La expansión del binomio de Newton constituye una herramienta poderosa para el cálculo de funciones generatrices.