MATEMÁTICAS DISCRETAS

PROFESOR:  JACINTO D'AVILA

REALIZADO POR: JUAN MANUEL USSHER

EMAIL: juanmussher@hotmail.com

    PREGUNTA No: 19

Notación y terminología:

    Este problema está planteado completamente en Español. Mediante Funciones Generatrices debe lograra demostrar lo solicitado.

Antecedentes:   

    Este problema y otros parecidos donde se utiliza las Funciones Generatrices pueden conseguirse en el libro "El Arte de Contar" de José Rodriguez.

PREGUNTA 19.

    Sea     Demuestre que:   

        Es el numero k-combinaciones con repetición de M donde cada elemento aparece un numero par de veces.

 

RESPUESTA 19.

    La suma de tales n-combinaciones, con m par, es el coeficiente de   en la expansión de:

 

 

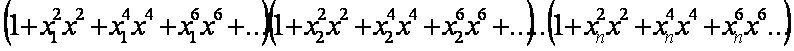
    Si hacemos   

   

                                  

    Y Hallamos: (1)

 

      

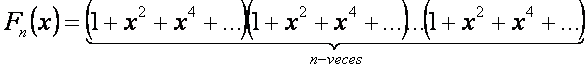
    Estos coeficientes vienen formado por:    tal que: 

    Con   enteros positivos pares.

    Pero por el Binomio de Newton sabemos que en general:

 

  

                                       

                                      

                                       

 

                                       

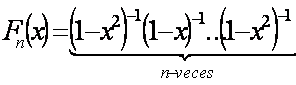
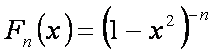
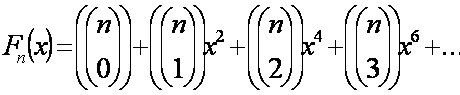
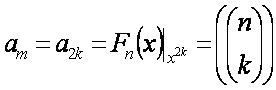
Moraleja: Las funciones generatrices son muy difíciles y abstractas pero con ayuda de ciertos desarrollos como el Binomio de Newton y otros pueden resolverse, siendo muy útiles para encontrar un numero combinatorio de interés.