Guía de Estudios de Matemática Discreta – Parcial 3.

Producida por

Jacinto Dávila <jacinto@ula.ve>

PROBLEMA 1

Notación y terminología: Este problema está planteado completamente en Español. Cuando se dice “rescatarlos con urgencia sacando uno por uno” significa que los objetos son extraídos a ciegas y son identificados cuando ya están afuera, sin posibilidad de devolverlos.

Antecedentes: Un problema similar, pero no idéntico, aparece en el libro del profesor José Rodríguez, El Arte de Contar, Capítulo 1. Ejercicio 14. Universidad de Los Andes.

PREGUNTA 1.

Tras el incendio, hay 10 libros de Francés, 22 en Español, 8 en Portugués, 5 en Arabe y 18 en Inglés, que quedaron en buen estado. Pero tenemos que rescatarlos con urgencia sacando uno por uno. ¿Cuántos tenemos que sacar hasta estar seguros de que tenemos 14 de una misma lengua?. Explique el porqué de su respuesta.

RESPUESTA 1.

En el peor escenario, habríamos de sacar los 10 libros de Francés, los 8 de Portugués, los 5 de Árabe y 13 tanto de Español como de Inglés, sin haber resuelto el problema. Uno más (que tendría que ser de Español o de Inglés, ¿Verdad?) sería suficiente. Es decir 10+8+5+13+14 = 50.

Noten que uno pudo haber sacado los 14 requeridos antes de eso. Pero A CIEGAS, el jefe de rescates puede decidir que tienen que sacar 50 por lo menos.

Moraleja: Es una mala idea aplicar las fórmulas de los números combinatorios sin pensar antes en el problema. Noten que un problema más complicado se plantea con la pregunta ¿De cuántas maneras se pueden sacar los libros para asegurar que se sacan 14 de una misma lengua?.

PROBLEMA 2

Notación y terminología: EISULA es el nombre de un centro de estudios. Si sirve de acrónimo para la Escuela de Ingeniería de Sistemas, es pura coincidencia. La palabra curso designa lo que comúnmente llamamos materia. Las dos únicas opciones en la discusión son computación y control.

Antecedentes: Al combinar conjuntos tenemos que tener presente los principios de inclusión y exclusión de los elementos comunes. De eso se trata la primera pregunta. La segunda es desafio de modelado que puede ser resuelto postulado como variable el número de cursos en cada semestre.

PREGUNTA 2.1:

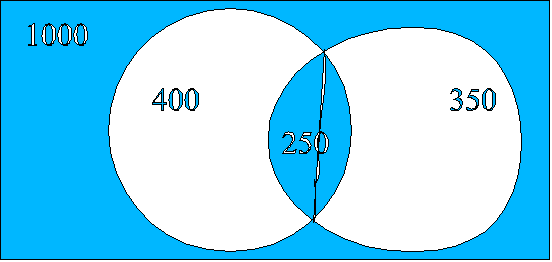
En EISULA hay 1000 estudiantes, 400 por computación, 350 por control y 250 por ambas 1)¿Cuántos estudiantes no toman ninguna de las 2?.

RESPUESTA 2.1

Es decir, 1000 – (400 + 350 – 250) = 500 son los estudiantes que no toman ninguna de las dos opciones.

PREGUNTA 2.2:

Hay 45 cursos en cada opción para distribuir en 9 semestres. ¿De cuántas maneras se puede hacer esta distribución, suponiendo que cada semestre hay al menos un curso?.

RESPUESTA 2.2:

Si cuenta el número de cursos en el semestre i, una formulación matemática podría ser:

con lo que el problema se reduce a encontrar todas las formas de resolver esa ecuación con números enteros positivos (pués debe haber al menos un curso en cada semestre, así que ningún puede ser cero.

Sabemos que el número de soluciones positivas enteras de esa ecuación es igual a la 9-composición de 45, C(45,9) (o partición ordenada de 45 de 9 en 9) y que su número es

PREGUNTA 2.3:

¿De cuántas maneras se puede hacer si no hay límite inferior al número de cursos por semestre?

RESPUESTA 2.3:

En este caso, siguen siendo útil el mismo modelo anterior, salvo que la restricción se relaja admitiendo que las pueden ser iguales a 0. En este caso, se trata del número de soluciones no-negativas de la misma ecuación que, según vimos en clases, es C(n+k, k). En este caso, k=9 y n=45. Es decir,

Moraleja: Sabemos contar el número de soluciones de una ecuación como las anteriores.

PROBLEMA 3

Notación y terminología:

Las combinaciones de N de M en M se designan con

Las permutaciones de N con N!.

Antecedentes:

Estas tres preguntas son típicos ejercicios de combinatoria aplicada a situaciones cotidianas.

PREGUNTA 3.1:

Una comisión de 5 personas se tiene que conformar en el seno del Consejo de Facultad, conformado por 10 hombres y 5 mujeres. ¿De cuántas maneras puede ser formada tal comisión si:

1. ¿Deben participar en ella al menos 2 mujeres y 1 hombre?

RESPUESTA 3.1:

Sin restricciones, las formas alternativas de formar la comisión de 5 personas sería de 15 tomados de 5 en 5, es decir, 3003 maneras. Así que ya tenemos una cota superior para nuestro número.

Para calcular el número consideramos la todas las maneras de satisfacer la restricciones.

Si son 2 mujeres y 3 hombres, las mujeres se escogen de maneras por las maneras de seleccionar a los hombres. Es decir, de 1200 maneras.

O puede ocurrir que sean 3 mujeres y 2 hombres. Combinaciones para las mujeres por combinaciones para las mujeres. Es decir, 450 maneras..

O, finalmente, puede ocurrir que sean 4 mujeres y 1 hombre. por 50 maneras.

El número total de formas de satisfacer la restriccion al seleccionar la comisión es, entonces, de 1200 + 450 + 50 = 1700.

Observen que si multiplicamos 5 de 2 en 2, por 10 de 1 en 1, por 12 de 2 en dos (7800) estaríamos modelando el problema en el que los que no son seleccionados en la primera etapa (las 3 mujeres restantes) y los que no son seleccionados en la segunda etapa (los 9 hombres restantes) vuelven a estar disponibles para selección en una tercera etapa de selección. Esto no es lo que se pretende modelar (No hay una tercera categoría, aparte de hombres y mujeres).

Lo que sí funciona es descontar de las 3003 maneras originales, las maneras en que se podría violar la restricción, es decir, si sólo participa 1 mujer (con 4 hombres), * o si son sólo hombres, o si son sólo mujeres . Es decir, 1303 maneras.

(Noten que 3003 – 1302 = 1701).

PREGUNTA 3.2:

5. ¿El Decano y uno de los directores de Escuela se rehusan a trabajar juntos?.

RESPUESTA 3.2:

Noten que nos olvidamos de división entre hombres y mujeres y tanto el decano como el director de Escuela pueden ser mujeres o hombres.

Las situaciones alternativas son: El decano participa, con lo que no participa el director, ó el director participa y el decano no, ó ninguno de los dos participa.

En el primer caso hay maneras, tal como en el segundo. Van 1430. En el último caso, hay maneras. En total, hay 2717 maneras.

De nuevo, podemos usar el caso complementario para verificar. Si ambos están, hay de escoger las tres restantes.

(Noten que 3003 – 286 = 2717).

PREGUNTA 3.3:

5. Queremos sentar a los miembros del Consejo en la mesa circular del Decanato, de manera que nunca haya 2 mujeres juntas ¿De cuántas formas podemos hacerlo?.

RESPUESTA 3.3:

Una forma práctica de llegar a la solución es considerar que los 10 hombres están ubicados en torno a la mesa con un espacio entre ellos (lo cuál ocurre de 9! maneras) y que las mujeres se deben ubicar entre los espacios entre ellos solamente. Esto es equivalente a la situación en la que seleccionamos 5 puestos de los 10 disponibles (con 10 hombres en el círculo, hay 10 espacios entre ellos). Pero una vez decididas las 5 posiciones, las mujeres pueden ser distribuidas en 5! maneras diferentes entre ellas.

Sin M es en número de hombres y N el de mujeres, la fórmula general es

Para M=3 y N = 2, tenemos 12 posibilidades. Gráficamente (con una salida generada por el computador):

========

... h1

m2 m1

h3

... h2

========

========

... h1

m1 m2

h3

.... h2

========

========

... h1

m2 m1

h2

... h3

========

========

... h1

m1 m2

h2

... h3

========

========

... h2

m2 m1

h3

... h1

========

========

... h2

m1 m2

h3

... h1

========

========

... h2

m2 m1

h1

... h3

========

========

... h2

m1 m2

h1

... h3

========

========

... h3

m2 m1

h2

... h1

========

========

... h3

m1 m2

h2

... h1

========

========

... h3

m2 m1

h1

... h2

========

========

... h3

m1 m2

h1

... h2

========

Moraleja:

En el cálculo combinatorio el sentido común puede ser muy útil.

PROBLEMA 4

Notación y terminología:

Antecedentes:

PREGUNTA 4.

Queremos estimar el número de Escuelas de Sistemas en Venezuela, considerando que la primera se fundó en 1960 y asumiendo que a cada nueva escuela le toma 5 años madurar hasta que de ella surge una nueva escuela. Una vez madura, una escuela “produce” otra nueva cada 5 años. Las Escuelas nunca se cierran y cada una produce 10 egresados cada año. ¿Cuántas Escuelas y Egresados hay en el 2000?. (EXPLIQUE)

Indicación: Esta secuencia puede ser útil (aunque no esté completa).

RESPUESTA 4.

Consideren la siguiente salida generada por el computador:

En 1960, etapa 1, hay 1,

con 0 maduras y 0 egresados.

En 1965, etapa 2, hay 1,

con 1 maduras y 0 egresados.

En 1970, etapa 3, hay 2,

con 1 maduras y 50 egresados.

En 1975, etapa 4, hay 3,

con 2 maduras y 100 egresados.

En 1980, etapa 5, hay 5,

con 3 maduras y 200 egresados.

En 1985, etapa 6, hay 8,

con 5 maduras y 350 egresados.

En 1990, etapa 7, hay 13,

con 8 maduras y 600 egresados.

En 1995, etapa 8, hay 21,

con 13 maduras y 1000 egresados.

En 2000, todavia etapa 8, antes de reproducirse, hay 21, con 21 maduras y 1650 egresados.

Es decir, En .., Etapa n, hay Fn escuelas, donde Fn es el número de Fibonacci.

El código PROLOG que hace esto es:

escuelas(A, B, C, F) :- N is (B-A)/C, fibo_bu1(A, C, 0, 0,0,1,N,F).

fibo_bu1(Base, C, Egresados, N,F,_,N,F) :-

write('En '), R is Base + C*N,

write(R), write(', todavia etapa '), write(N), write(','),

write(' antes de reproducirse, hay '), write(F), write(','),

write(' con '), write(F), write(' maduras y '), write(Egresados), writeln(' egresados.').

fibo_bu1(Base, C, E0, N1,F1,F2,N,F) :-

N1<N, N2 is N1+1, F3 is F1+F2,

Egresados is F1*10*C + E0,

write('En '), R is Base + C*N1,

write(R), write(', etapa '), write(N2), write(','),

write(' hay '), write(F2), writeln(','),

write(' con '), write(F1), write(' maduras y '), write(E0), writeln(' egresados.'),

fibo_bu1(Base, C, Egresados, N2,F2,F3,N,F).

y se puede describir así en ESPAÑOL:

El número de escuelas será F si el período va de A a B y las escuelas maduran cada C, y si N es la extensión de la serie sobre los números Fibonacci. Al N-esimo número de esa serie le corresponde el F de Fibonacci.

Moraleja:

Muchas de las teorias matemáticas más abstractas tienen un profundo sentido práctico.

PROBLEMA 5

Notación y terminología:

Este problema se plantea con código en Java (C o C++ tambiën sirve). Pero es una operación con estructura de repetición anidadas.

Antecedentes:

Hemos aprendido a contar todos los subconjuntos de cierto conjunto. También a contar los subconjuntos de un multi-conjunto. De esto último trata este problema.

PREGUNTA 5

Considere el siguiente segmento de programa Java, donde i, j y k son enteros.

int counter = 0;

for (int i = 1; i <= 20; i++) {

for (int j = 1; j <= i; j++) {

for (int k = 1; k <= j; k++) {

counter = counter + 1;

}

}

}

1. ¿Cuántas veces se ejecuta la instrucción counter = counter + 1?.

2. Si i no itera hasta 20, sino hasta un r desconocido, ¿Cuántas veces se ejecutaría?

RESPUESTA 5.

Observe la “traza” de ejecución de ese código (vaciando los valores de las variables).

i j k counter

1,1,1, 0

2,1,1, 1

2,2,1, 2

2,2,2, 3

3,1,1, 4

3,2,1, 5

3,2,2, 6

3,3,1, 7

3,3,2, 8

3,3,3, 9

4,1,1, 10

4,2,1, 11

4,2,2, 12

4,3,1, 13

4,3,2, 14

4,3,3, 15

4,4,1, 16

4,4,2, 17

4,4,3, 18

4,4,4, 19

5,1,1, 20

5,2,1, 21

5,2,2, 22

5,3,1, 23

5,3,2, 24

5,3,3, 25

5,4,1, 26

5,4,2, 27

5,4,3, 28

5,4,4, 29

5,5,1, 30

5,5,2, 31

5,5,3, 32

5,5,4, 33

5,5,5, 34

6,1,1, 35

6,2,1, 36

6,2,2, 37

6,3,1, 38

6,3,2, 39

6,3,3, 40

6,4,1, 41

6,4,2, 42

6,4,3, 43

6,4,4, 44

6,5,1, 45

6,5,2, 46

6,5,3, 47

6,5,4, 48

6,5,5, 49

6,6,1, 50

6,6,2, 51

6,6,3, 52

6,6,4, 53

6,6,5, 54

6,6,6, 55

7,1,1, 56

7,2,1, 57

7,2,2, 58

7,3,1, 59

7,3,2, 60

7,3,3, 61

7,4,1, 62

7,4,2, 63

7,4,3, 64

7,4,4, 65

7,5,1, 66

7,5,2, 67

7,5,3, 68

7,5,4, 69

7,5,5, 70

7,6,1, 71

7,6,2, 72

7,6,3, 73

7,6,4, 74

7,6,5, 75

7,6,6, 76

7,7,1, 77

7,7,2, 78

7,7,3, 79

7,7,4, 80

7,7,5, 81

7,7,6, 82

7,7,7, 83

8,1,1, 84

8,2,1, 85

8,2,2, 86

8,3,1, 87

8,3,2, 88

8,3,3, 89

8,4,1, 90

8,4,2, 91

8,4,3, 92

8,4,4, 93

8,5,1, 94

8,5,2, 95

8,5,3, 96

8,5,4, 97

8,5,5, 98

8,6,1, 99

8,6,2, 100

....

20,20,2, 1521

20,20,3, 1522

20,20,4, 1523

20,20,5, 1524

20,20,6, 1525

20,20,7, 1526

20,20,8, 1527

20,20,9, 1528

20,20,10, 1529

20,20,11, 1530

20,20,12, 1531

20,20,13, 1532

20,20,14, 1533

20,20,15, 1534

20,20,16, 1535

20,20,17, 1536

20,20,18, 1537

20,20,19, 1538

20,20,20, 1539

1540

Cada una de esas tripletas parece una selección de tres números consecutivos de la secuencia 20, 19, 18, 17, .. 3, 2, 1.

Para modelar la situación podemos pensar en los 3-submulticonjuntos de un conjunto M dado así:

Noten que el órden en la secuencia, ya es irrelevante. Cada uno de los 3-multconjuntos de M tiene la forma siguiente:

con

“de tal modo que contar todos los 3-multiconjuntos de M se reduce a contar todas las soluciones no negativas de esa ecuación que, según vimos en clase, se obtiene a través de:

Con n = 20 tenemos: 1540 tal como nos dice el contador al final. En el caso de que n=r, obviamente:

nos da la solución.

Moraleja:

La combinatoria de los multiconjuntos, o conjuntos con elementos repetidos, es también una herramienta práctica y puede ser muy útil en las evaluaciones de complejidad de los programas computacionales.

Fin de la evaluación