(Cálculo 30. Profesor Richard Rosales.)
Apuntes de Cálculo 30
Sección 1.1
Funciones reales de dos variables reales.
1.1.1 Motivación. A lo largo de las materias Cálculo 10 y Cálculo 20 se ha trabajado con funciones que dependen de una sola variable real. Estas se han graficado, se han estudiado los conceptos de límite, derivada, continuidad, integral y se han hecho aplicaciones de dichas funciones. Todo esto ha trascurrido en el plano rectangular. En esta materia vamos a hacer una extensión de estos conceptos, es decir, vamos a definir una función que depende de más de una variable real y por consiguiente, vamos a trabajar en un espacio de más de dos dimensiones. Particularmente nos vamos a centrar en el espacio tridimensional, que es donde podemos dibujar sin mucha dificultad y esto lo lograremos estudiando funciones que dependen de dos variables independientes y que generan un valor real.
Algunos ejemplos de este tipo de funciones los encontramos en los problemas de hallar áreas de figuras planas, como el área de un rectángulo que depende de las longitudes de sus lados (que son dos), en los problemas de hallar temperaturas en placas planas, donde los puntos de la placa se identifican con dos componentes (x,y) y en algunos casos esta temperatura depende del tiempo y por lo tanto la temperatura será una función de las dos componentes espaciales y del tiempo, es decir, tenemos una función de tres variables (x,y,t). Como los anteriores, existen innumerables ejemplos de funciones que dependen de dos o más variables.
1.1.2 Definición (Función real de dos variables reales). Sea D un conjunto de pares ordenados de números reales. Una función f real de dos variables reales es una correspondencia que asocia a cada par (x,y) en D un único número real que se denota por f(x,y). El conjunto D es llamado el dominio de f. El conjunto de todos los valores reales de la función es llamado el rango de la función.
Notación:
![]() ;
;
![]() .
.
Observación: Si z=f(x,y), decimos que x e y son las variables independientes y que z es la variable dependiente.
1.1.3
Definición (Gráfica de una
función real de dos variables reales). Dada una
función ![]() , definida por la regla z=f(x,y),
llamaremos gráfica de f a la gráfica de
la ecuación z=f(x,y), es decir, el conjunto de todas
las ternas ordenadas en el espacio de la forma (x,y,f(x,y)).
, definida por la regla z=f(x,y),
llamaremos gráfica de f a la gráfica de
la ecuación z=f(x,y), es decir, el conjunto de todas
las ternas ordenadas en el espacio de la forma (x,y,f(x,y)).
Gráfica
de ![]() =
=![]() .
.
La gráfica de f será por lo general, una superficie y como a cada par (x,y) del dominio le corresponde un único número z, cada recta perpendicular al plano xy que pase por el dominio de f, corta esta superficie en un único punto.
Ejemplo 1: Encuentre el dominio natural de la función dada por ![]() y
grafíquelo en el plano.
y
grafíquelo en el plano.
Solución:
Para que la regla tenga sentido se debe cumplir que ![]() . Esto
ocurre en el conjunto
. Esto
ocurre en el conjunto ![]() , es decir, el conjunto en el
plano, que está limitado por la parábola
, es decir, el conjunto en el
plano, que está limitado por la parábola ![]() y donde
la componente
y donde
la componente ![]() está por arriba de la
parábola (ver figura).
está por arriba de la
parábola (ver figura).
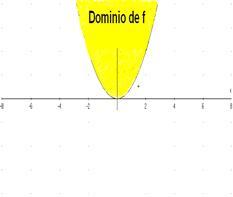
Gráfica del dominio de ![]()
Una forma rápida de decidir cual es el
conjunto que nos interesa, es tomar un punto (x,y) de un conjunto y
ver cuál es la desigualdad que se genera. En este ejemplo podemos tomar
el punto (0,1) que está en el conjunto situado sobre la parábola.
Luego ![]() ,
lo que nos indica que todos los puntos pertenecientes a dicho conjunto
satisfacen la desigualdad deseada.
,
lo que nos indica que todos los puntos pertenecientes a dicho conjunto
satisfacen la desigualdad deseada.
Ejemplo 2: Bosquejar la gráfica de la función ![]() en el
dominio
en el
dominio ![]() .
.
Solución: El dominio D consiste en los puntos del círculo de radio 2 centrado en el origen. La gráfica de la función es la parte del paraboloide que está por encima del plano xy.
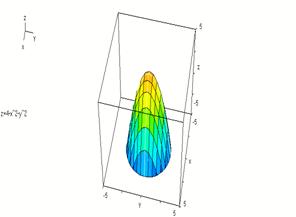
Un método gráfico útil para dibujar superficies en el espacio, consiste en trazar en el plano xy las curvas de nivel de la función f, las cuales se presentan en la siguiente definición.
1.1.4
Definición (curvas de nivel). Dada una función ![]() , definida por z=f(x,y), se definen
las curvas de nivel de f, como las gráficas de las
curvas definidas por las ecuaciones f(x,y)=k, para valores de k pertenecientes
al rango de la función.
, definida por z=f(x,y), se definen
las curvas de nivel de f, como las gráficas de las
curvas definidas por las ecuaciones f(x,y)=k, para valores de k pertenecientes
al rango de la función.
Ejemplo 3: Trazar las curvas de nivel de la función
![]() ,
,
en el dominio
![]() .
.
Solución: Las curvas de nivel son las gráficas de las ecuaciones ![]() , la
cual podemos reescribir como
, la
cual podemos reescribir como ![]() , es decir, son circunferencias de
radio
, es decir, son circunferencias de
radio ![]() cuando
cuando ![]() . En
el plano
. En
el plano ![]() algunas de las curvas de
nivel se verán como sigue:
algunas de las curvas de
nivel se verán como sigue:
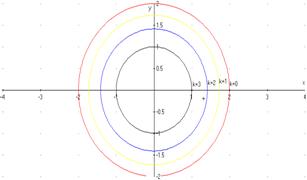
Curvas
de nivel de la función ![]()
Ejercicios:
1)
Determinar el dominio de ![]() y el valor de
y el valor de ![]() en los
puntos indicados:
en los
puntos indicados:
a) ![]()
b) ![]()
c) ![]()
2) Describir geométricamente el dominio de cada una de las siguientes funciones:
a) ![]()
b) ![]()
c) ![]()
3) Describir la gráfica
de ![]() :
:
a) ![]()
b) ![]()
c) ![]()
4)
Trazar algunas curvas de nivel de ![]() :
:
a) ![]()
b) ![]()
c) ![]()