(Cálculo 30. Profesor Richard Rosales.)
Apuntes de Cálculo 30
Sección 1.2
Función real de más de dos variables.
1.2.1
Definición (Función real de
más de dos variables reales). Sea 
un conjunto de
n-uplas de números reales. Una función 
real
de n variables reales es una correspondencia que asocia a cada
n-upla 
en un
único número real que se denota por 
. El conjunto es
llamado el dominio de . El conjunto de todos los valores
reales de la función denotados por 
es llamado el rango
de la función.
Notación:
;
.
Observación: Si 
, decimos que 
, son las
variables independientes y que 
es la variable dependiente.
1.2.2
Definición (Gráfica de una
función de más de dos variables reales). Dada una
función , definida por la regla 
,
llamaremos gráfica de al conjunto de todas las
(n+1)-uplas ordenadas en el espacio n+1 dimensional, que tienen la forma 
Gráfica
de =
.
Ejemplo 4: 
es una función de
tres variables. El dominio de la función es el conjunto de ternas
ordenadas 
que cumplen la desigualdad 
, o
equivalentemente 
, es decir, el dominio de , es
el conjunto de puntos del espacio situado dentro del elipsoide descrito por la ecuación
anterior.
Ejemplo 5: 
es una función de
cinco variables. El dominio de la función es el conjunto de 5-uplas
ordenadas 
que cumplen la desigualdad 
, o
equivalentemente 
. El dominio en este caso es una
región en el espacio pentadimensional y por lo tanto no lo podemos
representar gráficamente como en el caso del plano o el espacio
tridimensional.
Observación: Una superficie en el espacio tetradimensional no la podemos graficar en un sistema de coordenadas rectangular, pero podemos extender el concepto de curva de nivel para estas superficies. Aunque para el caso de dimensión cuatro, obtenemos superficies de nivel.
1.2.3
Definición (Superficies de nivel). Dada una función 
, definida por 
,
donde es el dominio de y
el
rango, se definen las superficies de nivel de la función , como
el conjunto de todas las superficies en 
de la forma 
,
donde 
.
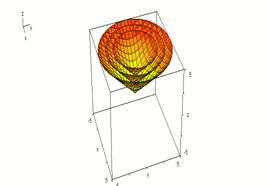
Ejemplo 6: Esbozar
algunas superficies de nivel de la función 
.
Solución:
Las superficies de nivel de la función , son
las gráficas de las ecuaciones 
, o equivalentemente, 
,
para cualquier número 
. Visto de otra forma tenemos 
, que
es la ecuación reducida de un cono circular recto con vértice en 
, con
su eje sobre el eje 
. Ver Figura.
1) Encuentre el dominio más amplio de las siguientes funciones:
a) 
b) 
c) 
d) 
e) 
2) Identifique algunas superficies de nivel de la siguiente función:
1.2.4 Algebra de funciones de varias variables.
Al igual que para funciones de una variable, podemos realizar operaciones con funciones de varias variables, teniendo en cuenta que la función resultante tiene por dominio, el dominio común a las funciones involucradas.
1.2.4.1
Definición: Sean 
y 
funciones
definidas por 
y 
respectivamente.
En el conjunto 
se definen las
siguientes funciones:
a) Función suma: 
definida
por 
b) Función producto: 
definida
por 
c)Función cociente:
En 
,
,
definida por 
1.2.5 Composición de funciones
1.2.5.1
Definición: Sea una función
real de varias variables reales y 
una función real de
una variable. Se define la función composición de con
como
la función 
para todo 
tal
que 
.
Ejercicios:
1) Encuentre la composición de las siguientes funciones:
a)
y
b)
y
c)
y
d)
y
e) 
y