(Cálculo 30. Profesor Richard Rosales.)
Apuntes de Cálculo 30
Sección 1.4
Continuidad de funciones
de varias variables.
La continuidad de funciones de varias variables,
nos permite calcular límites de una manera más rápida, en
los puntos donde ella es continua. Tal es el caso de las funciones polinomiales en dos o más variables, entre otras.
Pero en funciones de varias variables hablaremos de continuidad en puntos
interiores del dominio, así pues necesitamos conocer el concepto de
punto interior de un conjunto y otras definiciones importantes. En esta
sección, para simplificar un poco la notación, denotaremos los
puntos del espacio 
usando letras
mayúsculas del alfabeto latino.
1.4.1 Definición (Vecindad
de un punto). Dado un
número real 
y un punto 
, llamaremos vecindad
de 
al conjunto de
puntos 
en que satisfagan la
condición 
.
Ejemplo: En el plano 
, una vecindad de un punto es el interior de
un círculo centrado en . En el espacio
tridimensional, una vecindad de un punto es el interior de
una esfera centrada en .
1.4.2 Definición (punto
interior). Un punto es un punto interior de un conjunto 
si existe una
vecindad de contenida en .
1.4.3 Definición (interior).
El conjunto de todos los puntos interiores de un conjunto es llamado el interior de S.
1.4.4 Definición (punto
frontera). Un punto es llamado un punto frontera de un conjunto, si toda vecindad de contiene puntos
que pertenecen a y puntos que no
pertenecen a .
1.4.5 Definición (frontera).
El conjunto de todos los puntos frontera de un conjunto se conoce como frontera de .
1.4.6 Definición (abierto).
Un conjunto es llamado abierto si
todos sus puntos son interiores.
1.4.7 Definición (cerrado).
Un conjunto es llamado cerrado si
contiene todos sus puntos frontera.
Con esta terminología podemos dar la definición de
continuidad de funciones de varias variables. Consideremos una función 
, definida por 
.
1.4.8 Definición. Diremos que una función es continua en un punto interior 
de 
si se cumple que 
.
Ejemplo: La función 
es continua en
todo punto del plano. En efecto. 
, pues dado 
existe 
, tal que 
, si 
.
1.4.9 Definición. Una función se dice continua en un conjunto abierto si ella es
continua en todos los puntos de .
1.4.10 Proposición: Sean 
y 
funciones
continuas en el punto . Entonces:
a) 
es continua en
b) 
es continua en
c) 
es continua en si 
.
1.4.11 Proposición (composición
de funciones continuas).
Si una función real de varias variables es continua en el
punto y una
función real de una variable es continua en 
, entonces la composición 
, definida por 
es continua en .
Ejemplo: Muestre que la función 
es continua en
cada punto del plano.
Solución: La función 
es un polinomio y
por lo tanto es continua en cada punto 
del plano. Además,
la función 
es continua en
cada número real. Por la proposición 1.4.11 se concluye que la
función 
es continua en
cada punto del plano.
Ejercicios:
1) Describir el conjunto más grande donde cada una de las siguientes
funciones es continua.
a)
b)
c)
d)
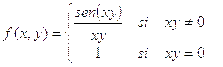
e)
