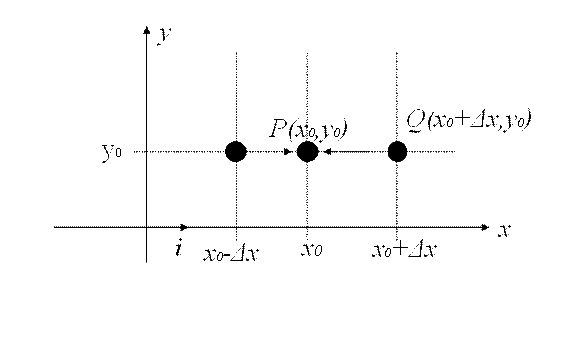(Cálculo 30. Profesor Richard Rosales.)
Apuntes de Cálculo 30
Sección 2.1
Derivada parcial y derivada direccional en un punto.
2.1.1
Motivación. En la sección anterior
aprendimos a calcular límites de funciones de varias variables. La
pregunta natural ahora es ¿ se puede calcular la derivada de una
función de varias variables?. La respuesta la daremos en lo que sigue.
Para ello, vamos a comenzar considerando a ![]() como una
función de dos variables x e y.
como una
función de dos variables x e y.
Tomemos ahora la
función ![]() , como aquella que evalúa a
, como aquella que evalúa a
![]() en
puntos que varían solo en su primera componente mientras que la segunda
permanece constante y tomemos la función
en
puntos que varían solo en su primera componente mientras que la segunda
permanece constante y tomemos la función ![]() , como la función
que evalúa a
, como la función
que evalúa a ![]() en puntos cuya segunda
componente varía mientras que la primera permanece constante. Como ahora
tenemos dos funciones de una sola variable, podemos preguntarnos acerca de la
derivada de dichas funciones, es decir, ¿existirán
en puntos cuya segunda
componente varía mientras que la primera permanece constante. Como ahora
tenemos dos funciones de una sola variable, podemos preguntarnos acerca de la
derivada de dichas funciones, es decir, ¿existirán ![]() y
y
![]() ?
La respuesta, como ustedes ya saben, será afirmativa si existe el
límite del cociente incremental estudiado en Calculo 20. Estos
límites son los siguientes:
?
La respuesta, como ustedes ya saben, será afirmativa si existe el
límite del cociente incremental estudiado en Calculo 20. Estos
límites son los siguientes:
![]() , (1)
, (1)
![]() . (2)
. (2)
Si los
límites (1) y (2) existen, entonces diremos que la función ![]() es
derivable en el punto
es
derivable en el punto ![]() con respecto a x e y
respectivamente, y estas derivadas serán llamadas derivada parcial con
respecto a x cuya notación será
con respecto a x e y
respectivamente, y estas derivadas serán llamadas derivada parcial con
respecto a x cuya notación será ![]() y
derivada parcial con respecto a y cuya notación será
y
derivada parcial con respecto a y cuya notación será
![]() respectivamente.
Escribamos la definición.
respectivamente.
Escribamos la definición.
2.1.2
Definición (Derivada parcial de f con
respecto a x). Sea f una función
real definida en un conjunto ![]() abierto. Sea
abierto. Sea ![]() un
punto interior de D. Diremos que el número L es la
derivada parcial de f con respecto a x en el punto
un
punto interior de D. Diremos que el número L es la
derivada parcial de f con respecto a x en el punto ![]() ,
si dado cualquier número
,
si dado cualquier número ![]() , existe un número
, existe un número ![]() tal que
tal que
![]() ,
si
,
si ![]() .
.
Observación:
La definición anterior no es otra cosa mas que el límite (1)
llamando L a ![]() .
.
Notación: ![]()
2.1.3
Definición (Derivada parcial de f con
respecto a y). Sea f una función
real definida en un conjunto ![]() abierto. Sea
abierto. Sea ![]() un
punto interior de D. Diremos que el número L es la
derivada parcial de f con respecto a y en el punto
un
punto interior de D. Diremos que el número L es la
derivada parcial de f con respecto a y en el punto ![]() ,
si dado cualquier número
,
si dado cualquier número ![]() , existe un número
, existe un número ![]() tal que
tal que
![]() ,
si
,
si ![]() .
.
Observación:
La definición anterior no es otra cosa mas que el límite (2)
llamando L a ![]() .
.
Notación: ![]()
Observación: La definición de derivada parcial está dada en términos de límites, mas sin embargo, en la práctica nosotros derivaremos con respecto a una sola variable, considerando la otra variable como una constante y así podremos usar las herramientas para derivar aprendidas en Calculo 20. Esto se pondrá en evidencia en el siguiente ejemplo.
Ejemplo 1: Encuentre las derivadas parciales con respecto a
x e y de la función f siguiente en cualquier
punto. ![]() .
.
Solución: El dominio D de la función f consiste en los
puntos del plano cartesiano. Por lo tanto, todos los puntos del dominio son
interiores. Sea ![]() .
.
![]() .
.
![]() .
.
Se puede observar claramente que hemos derivado la función, como si fuera una función de una sola variable en cada caso.
Ejemplo 2: Determinar ![]() y
y ![]() si
si ![]() .
.
Solución: El dominio D de la función f consiste en los
puntos del plano cartesiano. Por lo tanto, todos los puntos del dominio son
interiores. Sea ![]() .
.
![]() .
.
![]() .
.
Note que en este ejercicio hemos usado las técnicas de derivación para funciones de una variable, considerando en el primer caso a y como una constante y en el segundo a x.
Ejercicios:
1)
Determinar ![]() y
y ![]() en los puntos
indicados:
en los puntos
indicados:
a) ![]()
b) ![]()
c) ![]()
2) Hallar ![]() y
y ![]() para
cada una de las siguientes funciones. Describir geométricamente el
conjunto donde estas derivadas existan.
para
cada una de las siguientes funciones. Describir geométricamente el
conjunto donde estas derivadas existan.
a) ![]()
b) ![]()
c) ![]()
2.1.4 Interpretación geométrica de las derivadas parciales.
Consideremos la
función ![]() . Supongamos que esta
función genera una superficie S. Intersectemos esta superficie
con el plano
. Supongamos que esta
función genera una superficie S. Intersectemos esta superficie
con el plano ![]() . La intersección es una
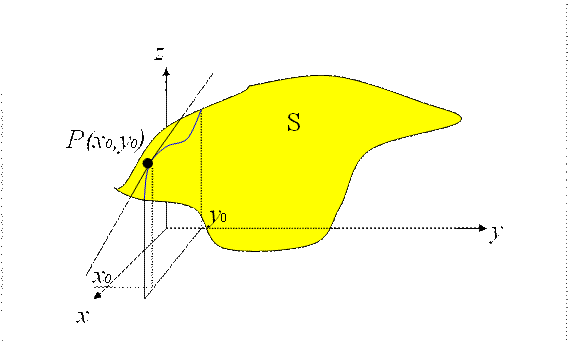
curva sobre las dos superficies. Dado el punto
. La intersección es una
curva sobre las dos superficies. Dado el punto ![]() sobre esta curva,
dibujemos la recta tangente a la curva en el punto P. La pendiente de la
recta tangente encontrada es la derivada parcial de f con respecto a y
(ver figura 1). De forma análoga tenemos que
la derivada parcial de f con respecto a x, es la pendiente de la
recta tangente a la curva generada por la intersección de la superficie
dada por f y el plano
sobre esta curva,
dibujemos la recta tangente a la curva en el punto P. La pendiente de la
recta tangente encontrada es la derivada parcial de f con respecto a y
(ver figura 1). De forma análoga tenemos que
la derivada parcial de f con respecto a x, es la pendiente de la
recta tangente a la curva generada por la intersección de la superficie
dada por f y el plano ![]() en el punto P (ver figura 2).
en el punto P (ver figura 2).
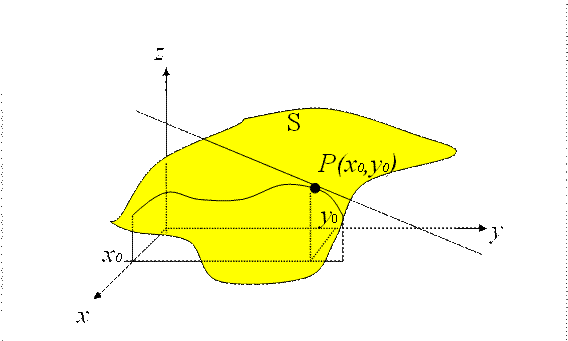
Figura 1
Figura 2
Note que cuando se calculan las derivadas parciales, se incrementa una sola variable, es decir, nos movemos a lo largo de alguna de las direcciones canónicas del plano xy. En la figura 3 se observa el caso en que nos movemos en la dirección del eje x para encontrar la derivada parcial con respecto a x, el punto Q tiende al punto P cuando Δx tiende a 0.
Figura 3
En la figura 4 se observa el caso en que nos movemos en la dirección del eje y para encontrar la derivada parcial con respecto a y, el punto Q tiende al punto P cuando Δy tiende a 0.
Figura 4
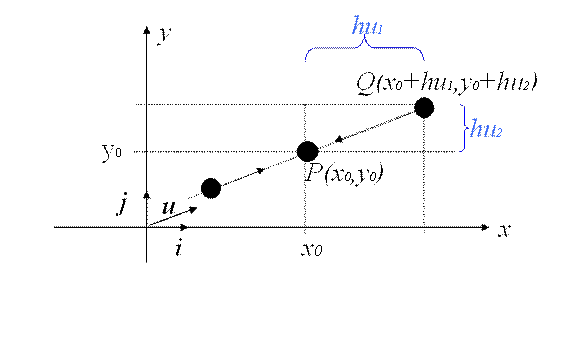
Es natural ahora pensar en acercarnos al punto P a lo largo de cualquier dirección distinta a las de los ejes coordenados. Es decir, que sucede con los límites (1) y (2) si nos acercamos al punto P a lo largo de una dirección unitaria que denotaremos por c. En la figura 5 podemos apreciar un esquema de lo que sucede. El punto Q se acerca al punto P a lo largo de la dirección de u. La distancia entre P y Q está denotada por h.
Figura 5
Si procedemos de esta manera, entonces vamos a estar calculando la derivada de la función f en el punto P pero en la dirección del vector unitario u. Esta será llamada derivada direccional.
2.1.5 Derivada direccional en un punto.
Sea ![]() una
función de dos variables definida en el conjunto abierto D. Sea
una
función de dos variables definida en el conjunto abierto D. Sea ![]() un
punto interior de D y
un
punto interior de D y ![]() una dirección
unitaria en el plano xy. Consideremos el siguiente límite
una dirección
unitaria en el plano xy. Consideremos el siguiente límite
![]()
Si este límite existe, entonces será llamado la derivada direccional de f en el punto P en la dirección de u.
Observación:
Note que si ![]() , entonces la derivada direccional
coincide con la derivada parcial con respecto a x. Y si
, entonces la derivada direccional
coincide con la derivada parcial con respecto a x. Y si ![]() ,
entonces la derivada direccional es precisamente la derivada parcial con
respecto a y.
,
entonces la derivada direccional es precisamente la derivada parcial con
respecto a y.
Ejemplo 3: Sea ![]() .
Calcular la derivada de f en el punto
.
Calcular la derivada de f en el punto ![]() en la
dirección del vector
en la
dirección del vector ![]() .
.
Solución:
Primero debemos encontrar un vector unitario en la dirección de ![]() . Para
ello, dividamos al vector
. Para
ello, dividamos al vector ![]() por su módulo.
Llamemos
por su módulo.
Llamemos ![]() a dicho vector. Entonces
a dicho vector. Entonces ![]() .
Ahora
.
Ahora ![]() =
=![]() =
= ![]() .
.
Ejemplo 4: Sea ![]() . Calcular la derivada de f en el punto
. Calcular la derivada de f en el punto ![]() en
la dirección de
en
la dirección de ![]() .
.
Solución:
Primero debemos encontrar un vector unitario en la dirección de ![]() . Para
ello, dividamos al vector
. Para
ello, dividamos al vector ![]() por su módulo.
Llamemos
por su módulo.
Llamemos ![]() a dicho vector. Entonces
a dicho vector. Entonces ![]() .
Ahora
.
Ahora
![]() =
= 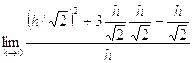 =
= 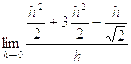 =
=
![]() =
= ![]() .
.
Observación: Más adelante, cuando estudiemos el vector gradiente, calcular derivadas direccionales será un juego de niños (bajo ciertas condiciones sobre f).
Ejercicios:
1)
Calcular la derivada direccional de la
función ![]() en el punto
en el punto ![]() en la
dirección del vector
en la
dirección del vector ![]() .
.
2)
Calcular la derivada direccional de la
función ![]() en el punto
en el punto ![]() en la
dirección del vector
en la
dirección del vector ![]() .
.
3)
Calcular la derivada direccional de la
función ![]() en el punto
en el punto ![]() en la
dirección del vector
en la
dirección del vector ![]() .
.
4)
Calcular la derivada direccional de la
función ![]() en el punto
en el punto ![]() en la
dirección del vector
en la
dirección del vector ![]() .
.
5)
Calcular la derivada direccional de la función
![]() en
el punto
en
el punto ![]() en la dirección del
vector
en la dirección del
vector ![]() .
.
2.1.6 Interpretación geométrica de las derivadas direccionales.
Como en el caso de las derivadas parciales, la derivada direccional de una función f en un punto P representa la pendiente de la recta tangente a la curva intersección de la superficie generada por f y el plano generado como un cilindro cuya directriz es el vector director u, en el punto P. Veamos esto de forma gráfica.
Consideremos la
función ![]() . Supongamos que esta
función genera una superficie S. Sea P un punto interior
del dominio de f y
. Supongamos que esta
función genera una superficie S. Sea P un punto interior
del dominio de f y ![]() un vector unitario en el
plano xy. Tracemos la recta l que es paralela al vector u y
que pasa por P. Luego, al dibujar rectas perpendiculares al plano xy
que pasen por la recta l (llamadas rectas generatrices del cilindro),
obtenemos un plano. Intersectemos la superficie S con el plano que hemos
generado. La intersección es una curva sobre las dos superficies. Dado
el punto
un vector unitario en el
plano xy. Tracemos la recta l que es paralela al vector u y
que pasa por P. Luego, al dibujar rectas perpendiculares al plano xy
que pasen por la recta l (llamadas rectas generatrices del cilindro),
obtenemos un plano. Intersectemos la superficie S con el plano que hemos
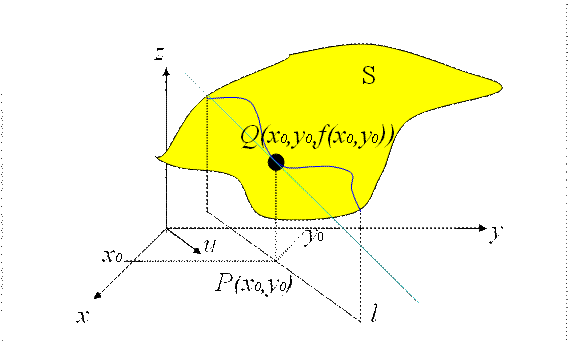
generado. La intersección es una curva sobre las dos superficies. Dado
el punto ![]() sobre esta curva, dibujemos
la recta tangente a la curva en el punto P (ver
figura 6). La pendiente de la recta tangente encontrada es la derivada
direccional de f en la dirección de u.
sobre esta curva, dibujemos
la recta tangente a la curva en el punto P (ver
figura 6). La pendiente de la recta tangente encontrada es la derivada
direccional de f en la dirección de u.
Figura 6