Destilación Flash de Sistemas No Ideales

El objetivo de este problema es mostrar como usar los modelos de coeficientes de actividad para describir las diferentes condiciones de operación de un equipo de destilación simple o flash Se tiene una alimentación de composición 30% molar en acetona(1) y 70% molar en n-hexeno que se quiere separar a través de una destilación súbita o flash a presión de 610 mmHg Seleccione el modelo termodinámico que mejor describe al sistema y determine a la presión de operación:

  1. Temperatura de Burbuja y composición de la primera burbuja
  2. Temperatura de Rocío y composición de la última gota
  3. Temperatura necesaria para evaporar el 30% de la alimentación y composición de las corrientes de salida

Contents

Preparación e introducción de datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura
% Declaramos todas las variables globales
global Ren
global A
global B
global C
global Pop
global k
global x
global y
global z
global fvap
Pop=610;                            % Presión de operación en torr o mmHg
Ren=1.987;                          % cal/mol/K

Selección del modelo

Vo=[74.05 84.161/.6731];            % Volumen molar en cm^3/mol
mu=[2.91     0];                    % Momento Dipolar a 20 ^oC en D
PM=[58.080 84.161];                 % Peso Molecular
omega=[0.307 0.280];                % Factor acéntrico
% Las desviaciones de la idealidad están causadas por una fuerte diferencia
% de polaridad entre las moléculas y una diferencia de tamaño moderada,
% puesto que difieren de la esfericidad en la misma cantidad
% Debido a la fuerte diferencia en polarida seleccionamos el modelo de
% Wilson

Modelo de Wilson

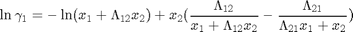
$$ \ln\gamma_1=-\ln (x_1 + \Lambda_{12} x_2)+x_2(\frac{\Lambda_{12}}{x_1+\Lambda_{12}x_2}-\frac{\Lambda_{21}}{\Lambda_{21}x_1+x_2})$$

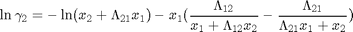
$$ \ln\gamma_2=-\ln (x_2 + \Lambda_{21}x_1)-x_1(\frac{\Lambda_{12}}{x_1+\Lambda_{12}x_2}-\frac{\Lambda_{21}}{\Lambda_{21}x_1+x_2})$$

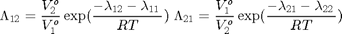
$$ \Lambda_{12}=\frac{V_2^o}{V_1^o}\exp(\frac{-\lambda_{12}-\lambda_{11}}{RT})$$ $$ \Lambda_{21}=\frac{V_1^o}{V_2^o}\exp(\frac{-\lambda_{21}-\lambda_{22}}{RT})$$

$$ k=[\lambda_{12}-\lambda_{11} \: \lambda_{21}-\lambda_{22}\: V_1^o \: V_2^o] $$

k=[1055.33888337994 38.8118860842799 Vo];  % Param. en cal/mol y cm^3/mol
% Los parámetros de Wilson fueron obtenidos por ajuste de data experimental
% tomada desde http://www.ddbst.com/en/EED/VLE/VLE%20Acetone%3B1-Hexene.php
% Ver archivo TxyAcetonanHexeno1atm.m

Determinación de la presión de vapor de compuestos puros

Usando la ecuación de Antoine 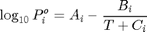$$ \log_{10}P_i^o=A_i-\frac{B_i}{T+C_i} $$ P en bar y T en K http://webbook.nist.gov/cgi/cbook.cgi?Name=1-hexene&Units=SI&cTC=on&cTP=on http://webbook.nist.gov/cgi/cbook.cgi?Name=acetone&Units=SI&cTC=on&cTP=on

A=[4.42448 3.99063];
B=[1312.253 1152.971];
C=[-32.445 -47.301];

Temperatura de Burbuja de la alimentación a la presión de operación

En el punto de burbuja se sabe que la cantidad de vapor formada es despreciable en relación a la alimentación, por lo que la composición de la fase líquida es aproximadamente igual a la de la alimentación

z=[0.3 0.7];                %Fracción Molar de acetona(1)-n-hexeno(2)
x=z;
% La temperatura de burbuja será aquella que permita alcanzar las
% condiciones del equilibrio termodinámico entre las fases líquido y vapor
% para la composición conocida a la presión de operación, definidas por las
% ecuaciones f_1 y f_2:

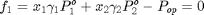
$$ f_1=x_1\gamma_1 P_1^o+x_2\gamma_2 P_2^o-P_{op}=0 $$

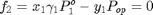
$$ f_2=x_1\gamma_1 P_1^o-y_1 P_{op}=0 $$

Debemos crear un archivo auxiliar llamado BurbujaWilson2.m con las ecuaciones de f_1 y f_2, donde T y y_1 son las incógnitas

Burbuja=fsolve(@BurbujaWilson2,[325 0.5])
% La temperatura de burbuja es 317.85 K y la composición de la primera
% burbuja es y_1=0.4626. No podrá obtenerse un destilado de composición
% superior a 46.3% molar en acetona por destilación en una etapa simple a
% la presión de operación

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




Burbuja =

   1.0e+02 *

   3.178507242204001   0.004625725960097

Temperatura de Rocio a la presión de operación

En el punto de rocío se sabe que la cantidad de líquido existente es despreciable en relación a la alimentación, por lo que la composición de la fase vapor es aproximadamente igual a la de la alimentación

Debemos crear un archivo auxiliar llamado RocioWilson2.m con las ecuaciones de f_1 y f_2, donde T y x_1 son las incógnitas

y=z;
% Debemos crear un archivo auxiliar llamado RocioWilson2.m con las
% ecuaciones de f_1 y f_2, pero donde T y x_1 son las incógnitas
Rocio=fsolve(@RocioWilson2,[328 0.5])
% La temperatura de rocío es 321.87 K y la última gota de líquido tiene una
% composición de 90.18 % molar en n-hexeno. No podrá obtenerse un producto
% de fondo de composición superior a 90.18% molar en n-hexeno por
% destilación en una etapa simple a la presión de operación

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




Rocio =

   1.0e+02 *

   3.218701081512530   0.000980604824662

Temperatura necesaria para evaporar el 30% de la alimentación

En este caso a las condiciones de equilibrio líquido-vapor se le suma la ecuación del balance de masas en el destilador

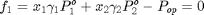
$$ f_1=x_1\gamma_1 P_1^o+x_2\gamma_2 P_2^o-P_{op}=0 $$

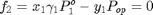
$$ f_2=x_1\gamma_1 P_1^o-y_1 P_{op}=0 $$

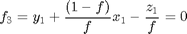
$$ f_3=y_1+\frac{(1-f)}{f}x_1-\frac{z_1}{f}=0 $$

Debemos crear un archivo auxiliar llamado FlashNoIdeal2.m con las ecuaciones de f_1, f_2 y f_3 pero donde T, x_1 y y_1 son las incógnitas

fvap=0.30
Vaporizacion30=fsolve(@FlashNoIdeal2,[326 0.5 0.5])
% La temperatura de operación para vaporizar el 30% de la alimentación es
% 318.43 K, y permite obtener un destilado(vapor) 43.38 % molar en acetona
% y un producto de fondo de 24.27 % molar en acetona (~ 75.73 %en n-hexeno)

fvap =

   0.300000000000000


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




Vaporizacion30 =

   1.0e+02 *

   3.184311828575037   0.002426803678212   0.004337458084173

Tarea

Resuelva el problema utilizando el método gráfico sabiendo que los datos al equilibrio del sistema acetona(1)-n-hexeno(2) a 610 mmHg son:

  1. x_1
  2. y_1
  3. T(K)
disp('x_1                     y_1                        T(K)');
disp([0                   0               329.864426811670;
        0.0500000000000000 0.200348940303143 324.616611859870;
        0.100000000000000 0.303022830049118 321.786884024348;
        0.150000000000000 0.364920355023409 320.113050677142;
        0.200000000000000 0.406803248462648 319.052124366538;
        0.250000000000000 0.437813968961155 318.343303067032;
        0.300000000000000 0.462572596011694 317.850724220521;
        0.350000000000000 0.483686658313216 317.499670421429;
        0.400000000000000 0.502782435279093 317.248018133764;
        0.450000000000000 0.520983225702364 317.072477907274;
        0.500000000000000 0.539157448523618 316.961649359537;
        0.550000000000000 0.558064936750288 316.912511313146;
        0.600000000000000 0.578459548137768 316.928838897652;
        0.650000000000000 0.601179652083386 317.020885413996;
        0.700000000000000 0.627249783639366 317.206112828693;
        0.750000000000000 0.658019299760550 317.511067366253;
        0.800000000000000 0.695377972563578 317.974831050585;
        0.850000000000000 0.742123103178153 318.654999151883;
        0.900000000000000 0.802634087090848 319.638131014557;
        0.950000000000000 0.884212606657654 321.058786407576;
        1                 1.00000000006370  323.136439325220]);

x_1                     y_1                        T(K)
   1.0e+02 *

                   0                   0   3.298644268116700
   0.000500000000000   0.002003489403031   3.246166118598700
   0.001000000000000   0.003030228300491   3.217868840243480
   0.001500000000000   0.003649203550234   3.201130506771420
   0.002000000000000   0.004068032484626   3.190521243665380
   0.002500000000000   0.004378139689612   3.183433030670321
   0.003000000000000   0.004625725960117   3.178507242205210
   0.003500000000000   0.004836866583132   3.174996704214290
   0.004000000000000   0.005027824352791   3.172480181337640
   0.004500000000000   0.005209832257024   3.170724779072740
   0.005000000000000   0.005391574485236   3.169616493595370
   0.005500000000000   0.005580649367503   3.169125113131460
   0.006000000000000   0.005784595481378   3.169288388976520
   0.006500000000000   0.006011796520834   3.170208854139960
   0.007000000000000   0.006272497836394   3.172061128286930
   0.007500000000000   0.006580192997605   3.175110673662530
   0.008000000000000   0.006953779725636   3.179748310505850
   0.008500000000000   0.007421231031782   3.186549991518830
   0.009000000000000   0.008026340870908   3.196381310145570
   0.009500000000000   0.008842126066577   3.210587864075760
   0.010000000000000   0.010000000000637   3.231364393252200


Published with MATLAB® R2012b