Equilibrio Líquido-Vapor de sistemas no ideales

El diagrama muestra un esquema simplificado para la producción de alcohol a partir de la fermentación de azucares.

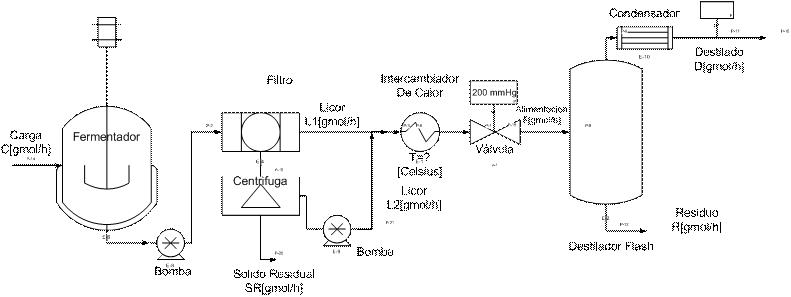
Como sabe. durante los procesos de fermentación controlados. las levaduras generan enzimas capaces de desdoblar las moléculas de azucares y

producir alcoholes. aldehídos y cetonas. La producción del etanol a partir de la glucosa puede representarse por la siguiente ecuación química:

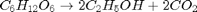
$C_6H_{12}O_{6} \rightarrow 2C_2H_5OH+2CO_2$

Preparación e Introducción de Datos
Balance de masa en el destilador Flash
Condiciones de ELV
Modelo de Energía Libre de Gibbs de Exceso
Resolución del sistema de ecuaciones
Solución
Tarea:

La carga a la salida del fermentador o cerveza posee un 11 % de alcohol en volumen (equivalente a una fracción molar de etanol en agua de 0.0367).

Si la presión de operación del destilador Flash es 200 mmHg. cual debería ser la temperatura a la salida de la válvula de estrangulamiento para lograr la producción de 3800 gmol/h de Destilado D con 10000 gmol/h de Residuo R. Cuales son las composiciones de todas las corrientes en el destilador.
Estime la cantidad mínima de azúcar en forma de glucosa en carga que debe existir para producir el destilado.
De poseer un segundo destilador Flash (operando a la misma presión y fracción de vaporización) cual seria la composición de destilado de salida?.
Considerando el rendimiento de este sistema. proponga alternativas para la producción de etanol absoluto usando destilación. Use toda la bibliografía que posea.

Preparación e Introducción de Datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura
% Creamos variables globales
global A
global B
global C
global Pop
global AVL
global z
global fvap
% La carga a la salida del fermentador o cerveza posee un 11 % de alcohol en volumen
z=[0.0367 1-.0367];                 % Composición de la alimentación al flash
Pop=200 ;                           % Presión de operación del flash en mmHg
V=3800;                             % Flujo molar de Destilado en mol/h
L=10000;                            % Flujo molar de Producto de Fondo en mol/h (Residuo)

Balance de masa en el destilador Flash

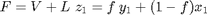
$F=V+L $$ $$ z_1=f\:y_1+(1-f)x_1$

F=V+L                               % Flujo molar de alimentación al Flash en mol/h
fvap=V/F                            % Fracción de vaporización

La relación entre el vapor y el líquido a la salida del destilador se corresponde con una fracción de vaporización de 27.54 % Se conoce la fracción de vaporización. f. z_A y la presión de operación del Flash pero se desconocen la temperatura y la composición de las corrientes de salida. para lo cual debemos considerar las condiciones del Equilibrio Líquido-Vapor (ELV)

Condiciones de ELV

Para cada componente se establece que al ELV se iguala la fugacidad molar parcial de cada compuesto en cada fase. por tanto:

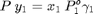
$P\:y_1=x_1\:P_1^o\gamma_1$

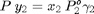
$P\:y_2=x_2\:P_2^o\gamma_2$

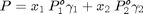
$P=x_1\:P_1^o\gamma_1+x_2\:P_2^o\gamma_2$

La presión de vapor de los componentes puros puede calcularse mediante la ecuación de Antoine:

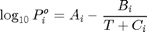
$\log_{10}P_i^o=A_i-\frac{B_i}{T+C_i}$

P en mmHg y T en ^oC

disp ('Compuesto       A            B           C')
disp('Etanol         8.1122     1592.864    226.184')
disp('Agua           8.07131    1730.63     233.426')
A=[8.1122 8.07131];
B=[1592.864 1730.63];
C=[226.184 233.426];

Modelo de Energía Libre de Gibbs de Exceso

La selección del modelo termodinámico para estimar la actividad de las especies en solución depende de la diferencia en forma. tamaño y polaridad de las sustancias en solución. Para ponderar la influencia de la forma comparamos el factor acéntrico de las moléculas (w). Recordemos que éste es una medida de la no esfericidad de la molécula en relación a las llamadas moléculas simples. Argón. Kriptón y Xenón (1): Etanol (compuesto más volátil) (2): Agua

w=[0.644 0.344];
dw=diff(w)./w(1).*100               % Diferencia porcentual respecto a (1)
% Para evaluar la diferencia en polaridad usamos el momento dipolar (mu)
mu=[1.73 1.86];                     % Momento Dipolar a 25 ^oC
dmu=diff(mu)./mu(1).*100            % Diferencia porcentual respecto a (1)
% Para evaluar la influencia del tamaño consideramos el peso molecular (PM)
% y el volumen molar del compuesto puro (Vo)en estado líquido a una temperatura
% determinada
PM=[46.07 18.015]                   % Peso Molecular g/mol
dPM=diff(PM)./PM(1).*100            % Diferencia porcentual respecto a (1)
rhoo=[0.789 1] ;                    % Densidad en g/mL
Vo=PM./rhoo                         % Volumen molar en mL/mol
dVo=diff(Vo)./Vo(1).*100            % Diferencia porcentual respecto a (1)

Las moléculas de etanol y agua son muy similares en polaridad (sólo difieren en un 7% una de otra). pero manifiestan diferencias moderadas en forma (~ 47%). y tamaño (60.9% en PM y 69.2% en Vo). Sabemos que tales diferencias ocasionarán desviaciones de la idealidad para la fase líquida. por lo que sus fugacidades serán superiores a las reportadas por la regla de Lewis-Randall. Debemos entonces seleccionar un modelo para estimar el coeficiente de actividad. Seleccionamos el modelo de van Laar por su sencillez y su buena representación del sistema etanol-agua Constantes de van Laar (Manual del Ingeniero Químico. Perry. Tomo IV)

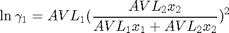
$\ln\gamma_1=AVL_1 (\frac{AVL_2x_2}{AVL_1x_1+AVL_2x_2})^2$

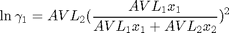
$\ln\gamma_1=AVL_2 (\frac{AVL_1x_1}{AVL_1x_1+AVL_2x_2})^2$

AVL=[1.6798 0.9927];

Resolución del sistema de ecuaciones

Se requiere resolver el sistema de tres ecuaciones con tres incógnitas (T. y_1. x_1) formado por el balance de masa y las condiciones de ELV. Para resolver este sistema debemos crear un archivo auxiliar FlashNoIdeal2VL.m

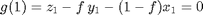
$g(1)=z_1-f\:y_1-(1-f)x_1 =0$

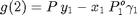
$g(2)= P\:y_1-x_1\:P_1^o\gamma_1$

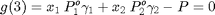
$g(3)= x_1\:P_1^o\gamma_1+x_2\:P_2^o\gamma_2 -P=0$

Con las siguientes ecuaciones auxiliares: 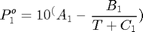$P_1^o=10^(A_1-\frac{B_1}{T+C_1})$

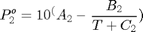
$P_2^o=10^(A_2-\frac{B_2}{T+C_2})$

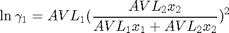
$\ln\gamma_1=AVL_1 (\frac{AVL_2x_2}{AVL_1x_1+AVL_2x_2})^2$

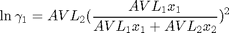
$\ln\gamma_1=AVL_2 (\frac{AVL_1x_1}{AVL_1x_1+AVL_2x_2})^2$

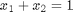
$$ x_1+x_2=1 $$

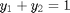
$$ y_1+y_2=1 $$

Empleamos el comando fsolve cuyos argumentos de entrada son el archivo de la función donde se encuentran las ecuaciones y las condiciones iniciales para cada incógnitas w=[T x_1 y_1]

solucion=fsolve(@FlashNoIdeal2VL.[70 0.1 0.6])

Solución

La temperatura de operación del Flash es de 64.18^oC. las corrientes de vapor y líquido a la salida del equipo tienen una composición molar en etanol de 10.7% y 1%. respectivamente. Para calcular la cantidad mínima de azúcar en forma de Glucosa que debe existir en la carga al fermentador es la definida por la estequiometría de la reacción:

$ C_6H_{12}O_{6} \rightarrow 2C_2H_5OH+2CO_2 $

Glucosa=F*z(1)*1/2                      % Flujo molar de glucosa mol/h

Para dar respuesta a la pregunta: De poseer un segundo destilador Flash (operando a la misma presión y fracción de vaporización) cual sería la composición de destilado de salida?. Debemos imaginar que el vapor a la salida del primer destilador se convierte en la alimentación al segundo destilador. De tal forma que resolvemos el mismo sistema de ecuaciones. pero cambiando la composición de la alimentación (z=y)

z=solucion(3)     % Fracción molar en etanol a la salida del 1er destilador
solucion2=fsolve(@FlashNoIdeal2VL.[50 0.01 0.9])

El segundo destilador debería operar a una temperatura de 59.74^oC y permitiría obtener una nueva corriente de vapor al 28.9 % molar en etanol y una corriente de líquido de 3.8% molar en etanol Como se observa esta no es la mejor manera de producir etanol de elevada pureza

Para conocer alternativas de producción de etanol absoluto usando destilación consulte el siguiente link: Deshidratación del etanol A.M. Uyazán ; I.D. Gil ; J.L. Aguilar ; G. Rodríguez ; L.A. Caicedo ; Ingeniería e Investigación 2004. 24 (3) http://www.redalyc.org/articulo.oa?id=64324308

Tarea:

Repita el problema pero de realice la solución gráfica considerando los siguientes datos para el ELV del sistema Etanol(1)-Agua(2) a 200 mHg

disp(' T(degC)       xA      yA')
disp('66.49532068	0       0')
disp('52.3371998	0.2     0.546680543')
disp('50.23357322	0.4     0.630337485')
disp('49.5539498	0.5     0.668515426')
disp('48.9711698	0.6     0.71247253')
disp('48.13302345	0.8     0.828403072')
disp('47.99154165	0.86	0.872836992')
disp('47.95801372	0.88	0.888862088')
disp('47.93175857	0.9     0.905542945')
disp('47.91306063	0.92	0.922911876')
disp('47.90221241	0.94	0.941003489')
disp('47.8995157	0.96	0.959854919')
disp('47.90015161	0.965	0.964691111')
disp('47.90528277	0.98	0.979506089')
disp('47.9188961	0.999	0.998954588')
disp('47.9198377	1       1')