Sistemas Ideales en equilibrio-vapor

Los líquidos A y B forman disoluciones ideales. Son isómeros, de modo que sus pesos moleculares son los mismos (y, por lo tanto sus fracciones en peso y molares). Una disolución de composición xA tiene una presión de vapor de 650mmHg a 50ºC. Se destila después (sin reflujo) hasta que la mitad se ha recogido como condensado. El condensado tiene una composición x’A igual a 0,60; y el líquido residual una composición x’’A de 0,40; y una presión de vapor de 600mmHg a 50ºC. Calcular la composición de la solución original y la presión de vapor de A y B como componentes puros. [1] Problemas de Química-Física, Arthur Adamson, Editorial Reverté, Madrid,

Contents

Preparación e introducción de datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura
% Creamos variables globales
global x
global y
global Pv_sol
global Pv_fon
global fvap
fvap=0.5;                              % Fracción de vaporización
% Se destila(sin reflujo) hasta que la mitad se ha recogido como condensado
% Las composiciones de las fases líquido(x) y vapor (y) están dadas
% Creamos vectores cuyas componentes son las fracciones molares de A y B
y=[0.6 1-0.6]; %El condensado tiene una composición x’A igual a 0,60
x=[0.4 1-0.4]; %El líquido residual una composición x’’A de 0,40
Pv_sol=650;                         % Presión de vapor de solución en mmHg
Pv_fon=600;                         % Presión de vapor de líquido residual en mmHg

Condiciones de ELV

Para cada componente se establece que al ELV se iguala la fugacidad molar parcial de cada compuesto en cada fase, por tanto:

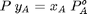
$$ P\:y_A=x_A\:P_A^o $$

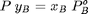
$$ P\:y_B=x_B\:P_B^o $$

Balance de masas en el compuesto más volátil

$$ x^p_A=f\:y_A+(1-f)x_A $$

Sistema de ecuaciones

Se establece un sistema de tres ecuaciones con tres incógnitas, donde:

w: Vector de incógnitas

  1. w(1): Presión de vapor de A a 50^oC
  2. w(2): Presión de vapor de B a 50^oC
  3. w(3): Fracción molar de A en la alimentación
  1. f(1)=@(w) x(1).*w(1)+x(2).*w(2)-P_{fondo}; % Ley de Raoult aplicada al líquido residual
  2. f(2)=@(w) w(3).*w(1)+(1-w(3)).*w(2)-P_{solucion}; % Ley de Raoul aplicada a la solución original
  3. f(3)=@(w) w(3)-fvap.*y(1)+(1-fvap).*x(1); % Balance de masas

Estas ecuaciones se escriben en un archivo de función llamado ELVIsomerosf.m

Este archivo DEBE ESTAR GUARDADO en la misma carpeta de trabajo donde se encuentre el archivo de este problema

Resolución del sistema de ecuaciones

Usamos la función fsolve de MatLab y usamos un vector de condiciones iniciales

soluciones=fsolve(@ELVIsomerosf,[400 200 0.5])

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




soluciones =

   1.0e+02 *

   9.000000000000002   4.000000000000000   0.005000000000000

Solución al problema

Las presiones de vapor de A y B son respectivamente 900mmHg y 400 mmHg La fracción molar de A en la solución original es 0.5


Published with MATLAB® R2012b