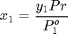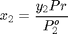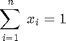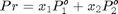Contents

Equilibrio líquido-vapor de sistemas ideales

Se tiene una mezcla equimolar de 1-propanol y 2-propanol a la Temperatura de 60^oC. Calcule:

  1. Presión de rocío de la solución
  2. Presión de burbuja de la solución
  3. La proporción de Vapor y Líquido, y sus respectivas composiciones ... cuando la mezcla se somete a una presión igual al promedio aritmético entre la Presión de Burbuja y la Presión de Rocío.

La presión de vapor de los componentes puros puede calcularse mediante la ecuación de Antoine:

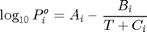
$$ \log_{10}P_i^o=A_i-\frac{B_i}{T+C_i} $$

P en mmHg y T en ^oC

disp ('Compuesto       A       B       C')
disp('1- Propanol     8,37895	1788,02	227,438')
disp('2- Propanol     8,87829	2010,32	252,636')
%

Compuesto       A       B       C
1- Propanol     8,37895	1788,02	227,438
2- Propanol     8,87829	2010,32	252,636

Preparación e introducción de datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura
% Debemos chequear que el iso-propanol es más volátil que el 1-propanol
% Definimos que: (1):2-propanol (2):1-propanol
A=[8.87829 8.37895 ];
B=[2010.32 1788.02 ];
C=[252.636 227.438 ];
z=[0.5 1-0.5];                      % Composición de la solución original
T= 60;                              % Temperatura del sistema (constante)

Modelo descriptivo para el ELV

El sistema 1-propanol/2-propanol se comporta a la temperatura de 60^oC puede modelarse usando la ecuación de gas ideal para la fase vapor (presiones de vapor de los compuestos muy por debajo de la presión crítica), y la ecuación de Raoult para la fase líquida (sustancias muy similares en forma, tamaño y polaridad; cuya presión de vapor está cercana a la presión total del sistema).

Presión de burbuja (Pb)

A temperatura constante, la presión de vapor de los compuestos puros permanece constante. La calculamos usando la ecuación de Antoine

P1vap=10.^(A(1)-B(1)./(T+C(1))); % mmHg
P2vap=10.^(A(2)-B(2)./(T+C(2))); % mmHg

En el punto de burbuja la composición del líquido no difiere de aquella de la solución original

x=z;
Pb=x(1)*P1vap+x(2)*P2vap
yb=x(1)*P1vap/Pb

Pb =

     2.123001271754318e+02


yb =

   0.660821530054008

La presión de burbuja es de 212.3 mmHg y la primera burbuja de vapor por expansión isotérmica tiene una composición molar de en 1-propanol de 66.1% (máxima posible para el vapor proveniente de la destilación de la solución original)

Presión de rocío (Pr)

En el punto de rocío, la composición del vapor no difiere de aquella de la solución original, y la composición del líquido es desconocida

y=z;
  1. $$ x_1=\frac{y_1Pr}{P^o_1} $$
  2. $$ x_2=\frac{y_2Pr}{P^o_2} $$

Uniendo las ecuaciones 1 y 2 debe cumplirse que:

  1. $$ \sum_{i=1}^n\:x_i=1 $$
  2. $$ Pr=x_1P^o_1+x_2P^o_2 $$

Si mezclamos ambas ecuaciones, tendremos una ecuación con una sola incógnita, x_1, que nos permitirá definir la función a resolver

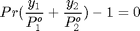
$$ Pr(\frac{y_1}{P^o_1}+\frac{y_2}{P^o_2})-1=0$$

f=@(x1) (x1*P1vap+(1-x1)*P2vap)*(y(1)/P1vap+y(2)/P2vap)-1;
xrocio=fsolve(f,0.2)
Pr=xrocio*P1vap+(1-xrocio)*P2vap

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




xrocio =

   0.339178470112729


Pr =

     1.903367750434110e+02

La presión de rocio es 190.34 mmHg y la última gota de líquido (durante expansión isotérmica) tiene una composición de 33.92% de 2-propanol, o sea 66.08 % molar en 1-propanol (máxima posible para el líquido proveniente de la destilación de la solución original)

Destilación Flash a T=60^oC y P=(Pb+Pr)/2

P=mean([Pb Pr])        % Presión promedio entre la de burbuja y rocío

P =

     2.013184511094214e+02

En este caso deben satisfacerse las ecuaciones del balance de masa y del equilibrio líquido-vapor:

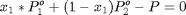  1. $$ x_1*P^o_1+(1-x_1)P^o_2 -P =0$$
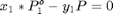
  2. $$ x_1*P^o_1-y_1P=0 $$
  3. $$ f_{vap}y_1+(1-f_{vap})x_1-z_1=0 $$

Se tienen tres ecuaciones con tres incógnitas: x_1, y_1, fvap Creamos un archivo auxiliar llamado ELVnPropisoPropanolf.m Este archivo DEBE ESTAR GUARDADO en la misma carpeta de trabajo donde se encuentre el archivo de este problema

Resolución del sistema de ecuaciones

Usamos la función fsolve de MatLab y usamos un vector de condiciones iniciales. Debemos crear variables globales para facilitar la resolución

global z
global P
global P1vap
global P2vap
soluciones=fsolve(@ELVnPropisoPropanolf,[0.5 0.5 0.5])

Warning: The value of local
variables may have been
changed to match the
         globals.  Future
         versions of MATLAB
         will require that
         you declare
         a variable to be
         global before you
         use that variable. 
Warning: The value of local
variables may have been
changed to match the
         globals.  Future
         versions of MATLAB
         will require that
         you declare
         a variable to be
         global before you
         use that variable. 
Warning: The value of local
variables may have been
changed to match the
         globals.  Future
         versions of MATLAB
         will require that
         you declare
         a variable to be
         global before you
         use that variable. 
Warning: The value of local
variables may have been
changed to match the
         globals.  Future
         versions of MATLAB
         will require that
         you declare
         a variable to be
         global before you
         use that variable. 

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




soluciones =

   0.419589235056365   0.584797074312514   0.486724875191714

La destilación Flash de la solución equimolar a la presión de 201.3 mmHg y 60^oC permite obtener un líquido con una composición molar 41.95% y un vapor de composición molar 58.5% molar en 2-propanol, logrando un 48.7% de vaporización. Observamos que la separación no es eficiente, puesto que los compuestos tienen volatilidades similares. La volatilidad relativa a 60 ^oC es sólo de 1.95 (\alpha)


Published with MATLAB® R2012b