Equilibrio Líquido-Vapor de soluciones de acetona(1) y cloroformo(2)

8. Se dispone de los siguientes datos para las soluciones de acetona y cloroformo a 50ºC: Calcular los coeficientes de actividad de ambos componentes y trazar su gráfica conforme a las expresiones de Van Laar para determinar las constantes empíricas del sistema (A y B). ¿Tienen alguna interpretación los coeficientes de Van Laar en función de las interacciones entre componentes de las soluciones?

Contents

Preparacion

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura

Introducción de datos

Primera columna: fracción molar en acetona x_1 en fase líquida Segunda columna: fracción molar en acetona y_1 en fase vapor Tercera columna: presión de equilibrio en mmHg

xyP=[0.00	0.00	521;
    0.1	0.071	495;
    0.2	0.165	474;
    0.3	0.279	463;
    0.38 0.38	458;
    0.4	0.408	460;
    0.5	0.55	469;
    0.6	0.684	489;
    0.7	0.789	511;
    0.8	0.89	540;
    0.9	0.955	576;
    1	1	612];
% Creamos un arreglo de columnas para la composición del líquido
% La primera columna contiene la fracción molar en acetona, la segunda en
% cloroformo. No tomamos ni la primera ni la última fila porque contienen la
% presión de vapor de los compuestos puros
x=[xyP(2:end-1,1) 1-xyP(2:end-1,1)];
y=[xyP(2:end-1,2) 1-xyP(2:end-1,2)];
P=xyP(2:end-1,3);

Determinación de la presión de vapor de compuestos puros

P1vap=xyP(end,3); % Pvap de acetona en mmHg
P2vap=xyP(1,3);   % Pvap de cloroformo en mmHg

Determinación de los coeficientes de actividad

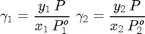
$$ \gamma_1=\frac{y_1\:P}{x_1\:P_1^o} $$ $$ \gamma_2=\frac{y_2\:P}{x_2\:P_2^o} $$

Para todos los cálculos usamos los operadores precedidos de punto ya que necesitamos operaciones elemento a elemento

gamma1=y(:,1).*P./(P1vap.*x(:,1));
gamma2=y(:,2).*P./(P2vap.*x(:,2));

Representación gráfica de resultados

figure
plot(x(:,1), gamma1, '+-b', x(:,1), gamma2, '*-r')
xlabel('Fracción molar en fase líquida x_1')
ylabel('\gamma_1 & \gamma_2')
title('ELV acetona(1)/cloroformo(2) a T=50^oC')
grid on
% El sistema presenta desviaciones negativas de la idealidad
% Para cada compuesto la fugacidad en solución es inferior a la que tendría
% en una solución ideal de la misma composición a la misma T y P

Determinación de la Energía Libre de Gibbs de Exceso

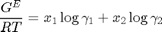
$$ \frac{G^E}{RT}=x_1\log \gamma_1+x_2\log \gamma_2 $$

GERT=x(:,1).*log(gamma1)+x(:,2).*log(gamma2);
GERTx1x2=GERT./x(:,1)./x(:,2);
x1x2GERT=1./GERTx1x2;
% Las desviaciones de la idealidad son negativas y sugieren que no hay una
% influencia significativa de la forma y tamaño en las moléculas, puesto que
% la parábola G^E/RT es casi simétrica alrededor de su foco.
% Las desviaciones de la idealidad están causadas por una fuerte diferencia
% de polaridad entre las moléculas

Representación gráfica de resultados

figure
plot(x(:,1), GERT, '+-b')
xlabel('Fracción molar en fase líquida x_1')
ylabel('GE/RT')
title('ELV acetona(1)/cloroformo(2) a T=50^oC')
grid on

Aplicación del modelo de van Laar

El modelo de van Laar establece que: $$ \frac{x_1x_2}{\frac{G^E}{RT}}=\left(\frac{1}{A_{21}}-\frac{1}{A_{12}}\right)x_1+\frac{1}{A_{12}} $

Y=x1x2GERT;                   % Variable dependiente a modelar
X=x(:,1);                     % Variable independiente a modelar
gradoPolinomio=1;             % Se requiere una línea recta Y=Pendiente*X+Corte
b=polyfit(X,Y,gradoPolinomio) % b contiene coeficientes del polinomio (pendiente y corte)
Ycalc=polyval(b,X)            % Estimamos las predicciones del modelo
Residuos=Y-Ycalc;             % Estimamos los errores de las predicciones
% Análisis de la bondad del ajuste
whichstats={'rsquare', 'adjrsquare', 'fstat'};
stats=regstats(Y,X,'linear', whichstats);
r2=stats.rsquare        % Factor de correlación o r cuadrado debe estar cercano a 1
adjr2=stats.adjrsquare  % Factor de correlación ajustado debe estar cercano a 1 y a r2
valorp=stats.fstat.pval % Valor p para el análisis de varianza de la regresión p<\alpha, \alpha=0.05

b =

  -0.099585233228802  -1.229992936114284


Ycalc =

  -1.239951459437164
  -1.249909982760044
  -1.259868506082924
  -1.267835324741229
  -1.269827029405805
  -1.279785552728685
  -1.289744076051565
  -1.299702599374445
  -1.309661122697325
  -1.319619646020205


r2 =

   0.250518308796628


adjr2 =

   0.156833097396207


valorp =

   0.140635702095649

Representacion grafica de los resultados

figure
plot(x(:,1), x1x2GERT, '+b', x(:,1), Ycalc,'*-r')
xlabel('Fracción molar en fase líquida x_1')
ylabel('x_1x_2/(GE/RT))')
title('ELV acetona(1)/cloroformo(2) a T=50^oC')
grid on
legend('Exp','Ajuste van Laar')

Conclusión

El modelo de van Laar no representa adecuadamente el ELV del sistema acetona-cloroformo a 50 ^oC tal como se esperaba, puesto que éste presenta desviaciones negativas de la Ley de Raoult, y el modelo de van Laar sólo es capaz de describir desviaciones positivas Sin embargo notamos que las constantes de van Laar son ambas negativas guardando una relación con el tipo de desviaciones mostradas por el sistema Estas constantes tienen un valor de

A12=1/b(2)
A21=(b(1)+b(2))^(-1)
% La literatura(Perry, 1998) reporta las constantes de A12=-0.8343 y A21=-0.5899
% para este mismo sistema

A12 =

  -0.813012799210975


A21 =

  -0.752118245513972


Published with MATLAB® R2012b