Equilibrio de Fases de Sustancias Puras

Contents

Algo de teoría

Recordemos que si una sustancia pura se somete a una transformación de fases cualquiera, donde \alpha y \beta representan estados de existencia característicos, por ejemplo una vaporización de \alpha=líquido a \beta=vapor:

El equilibrio termodinámico para esta transformación se alcanza cuando se cumplen las tres condiciones:

  1. $$ T^\alpha=T^\beta=T $$
  2. $$ P^\alpha=P^\beta=P $$
  3. $$ G^\alpha=G^\beta $$

Al satisfacerse estas tres relaciones se está garantizando el cumplimiento de las leyes de la termodinámica, y la ausencia de gradientes finitos de presión que pudieran conducir a la transferencia de cantidad de movimiento, la ausencia de gradientes finitos de temperatura que pudieran conducir a la transferencia de energía en forma de calor, o y la ausencia de gradientes finitos de energía libre de Gibbs molar (potencial químico) que pudieran conducir a la transferencia neta de masa en la interfase \alpha-\beta (el cambio de masa de una fase que describe lo ganado es exactamente igual a lo que pierde la segunda) En el equilibrio termodinámico a una temperatura T y presión P correspondientes, se debe cumplir que:

  1. $$ dG^\alpha=dG^\beta $$
  2. $$ -S^\alpha dT + V^\alpha dP =-S^\beta dT + V^\beta dP $$
  3. $$ \frac{dP}{dT}=\frac{S^\beta-S^\alpha}{V^\beta-V^\alpha}=\frac{\Delta S^{\beta\rightarrow\alpha}}{\Delta V^{\beta\rightarrow\alpha}} $$

Esta última ecuación es la ecuación de Clasius y puede ser aplicada a cualquier transformación de fase. En los casos particulares de la sublimación y la evaporación puede ser transformada en la ecuación de Clasius-Clapeyron si se realizan las siguientes aproximaciones:

  1. $$ \Delta S^{\beta\rightarrow\alpha}=\frac{\Delta H^{\beta\rightarrow\alpha}}{T} $$
  2. $$ \Delta V^{\beta\rightarrow\alpha}\sim V^{\beta} $$
  3. $$ V^{\beta}=V^{vapor}=\frac{RT}{P} $$

La ecuación de Clasius-Clapeyron describe la relación entre la presión y temperatura del equilibrio termodinámico para la sublimación o la vaporización, y sus procesos inversos, siempre y cuando, se cumplan las condiciones establecidas, es especial la de comportamiento de gas ideal para la fase vapor involucrada

  1. $$ \frac{dP}{dT}=\frac{\Delta H^{\beta\rightarrow\alpha}P}{RT^2} $$
  2. $$ \log P = -\frac{\Delta H^{\beta\rightarrow\alpha}}{RT}+Ctte $$

El siguiente conjunto de problemas se enfoca en la aplicabilidad de ambas ecuaciones, y de su importancia para predecir las condiciones necesarias para el establecimiento del equilibrio termodinámico de la transformación de fases de una sustancia pura

Problemas de repaso extraídos de: Ball, David Fisicoquímica (2004) México: Thomson https://books.google.co.ve/books/about/Fisicoqu%C3%ADmica.html?hl=es&id=HNJqPBFNa_0C&redir_esc=y

Problema sobre Equilibrio Sólido-Líquido

Ejemplo 6.4 página 149 Calcule la presión que se requiere para fundir el agua a -10oC si el volumen molar del agua en estado líquido es de 18.01 mL y el volumen molar del hielo es de 19.64 mL. El valor de \Delta S para este proceso es de 22.04 J/K; puede suponer que estos valores permanecen relativamente constantes con respecto a la temperatura. Se necesitará el siguiente factor de conversión: 1Lbar =100 J Preparación e introducción de datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
Po=1.01325;                         % Presión en bar para estado inicial
DeltaT=-10;                         % Cambio esperado para la temperatura de fusión (-10-0)^oC
DeltaS=22.04;                       % Entropía de fusión del agua a 0^oC y Po
V=[19.64 18.01]/1000;               % volumen molar en L/mol para sólido y líquido a 0^oC y Po
DeltaV=diff(V)                      % Calculamos el cambio de volumen de fusión
% Notamos que la fusión del agua implica una reducción del espacio ocupado
% por un mol de la sustancia

DeltaV =

  -0.001630000000000

Usamos la ecuación de Clasius suponiendo constancia en la entropía de fusión y el cambio de volumen molar en el intervalo [0^oC, -10^oC]

DeltaP=DeltaS/DeltaV/100*DeltaT; % Usamos el factor de conversión 1Lbar =100J
Pf=Po+DeltaP

Pf =

     1.353160489263804e+03

Para que la fusión del hielo se realice a -10oC se requiere de una presión equivalente a ~ 1350 bar

Problema sobre cambio de fase en estado sólido (Alotropía)

Ejemplo 6.5 página 150 Estime la presión necesaria para obtener diamante a partir de grafito a una temperatura de 2298 K con \Delta T =(2298-298)K=2000 K. (Esta conversión se la consiguió a nivel industrial, por primera vez General Electric en 1955). Se necesitará el siguiente factor de conversión: 1Lbar =100 J Utilice la siguiente información

    $$ C_{s, grafito}\rightarrow C_{s,diamante}$$
  1. S(J/mol/K) 5.69 2.43
  2. V(L/mol) 4.41E-03 3.41E-03

Entre las formas alotrópicas del carbono están el grafito (b) y el diamante (a)

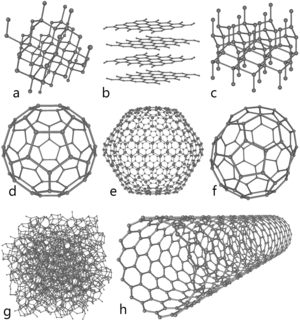
Tomado desde: https://commons.wikimedia.org/wiki/File:Eight_Allotropes_of_Carbon.png#/media/File:Eight_Allotropes_of_Carbon.png

Preparación e introducción de datos

clear all                           % Borramos toda posible variable que venga del problema anterior
clc                                 % Limpiamos la pantalla de comando
S=[5.69 2.43] ;                     % Entropía molar de grafito y diamante a 298 K y 1 atm en J/K/mol
V=[4.41 3.41]/1000;                 % volumen molar en L/mol para grafito y diamante a 298K y 1 atm en L/mol
Po=1.01325;                         % Presión en bar para estado inicial
T=[298 2298];                       % Cambio de Temperatura requerido para la transformación de fases
DeltaT=diff(T)                      % Calculamos el cambio de temperatura
DeltaV=diff(V)                      % Calculamos el cambio de volumen molar durante la transformacion de fases
DeltaS=diff(S)                      % Calculamos el cambio de entropía molar durante la transformacion de fases
% Usamos la ecuación de Clasius para la transformación de fases del carbono
% entre sus formas alotrópicas
DeltaP=DeltaS/DeltaV/100*DeltaT; % Usamos el factor de conversión 1Lbar =100J
Pf=Po+DeltaP
% Para lograr la transformación de fases de grafito a diamante a 2298 K se
% requiere una presión aproximada de 65200 bar.
% Para información adicional consulte:
% https://es.wikipedia.org/wiki/Al%C3%B3tropos_del_carbono
% http://www.ige.org/gemologia/diamantes/diamantes-sinteticos/
% http://www.bbc.com/mundo/noticias/2014/03/140312_elementos_diamantes_finde

DeltaT =

        2000


DeltaV =

    -9.999999999999996e-04


DeltaS =

  -3.260000000000000


Pf =

     6.520101325000003e+04

Equilibrio de Fases Líquido-Vapor

Ejercicio Propuesto 6.30 ¿A qué presión alcanza los 300^oC el punto de ebullición del agua? Si la presión del oceano se incrementa 1 atm cada 10 m ¿qué profundidad del oceáno corresponde a esta presión? ¿Existen dichas profundidades oceánicas en este planeta? ¿cuáles son las implicaciones potenciales de los volcanes sumergidos en el mar? Preparación e introducción de datos

clear all                           % Borramos toda posible variable que venga del problema anterior
clc                                 % Limpiamos la pantalla de comando
Rene=8.314;
S=[1.3072 7.3542]*18 ;              % Entropía molar en J/mol/K líquido y vapor saturados a 100oC y 1 atm (Tablas)
V=[0.001043 1.6720]*18;             % volumen molar en L/mol líquido y vapor saturados a 100oC y 1 atm (Tablas)
H=[419.17 2675.6]*18;               % Entalpía molar de líquido y vapor saturados a 100oC y 1 atm (Tablas)
Po=1.01325;                         % Presión en bar para estado inicial
T=[100 300]+273.15                  % Cambio de Temperatura requerido para la transformación de fases
DeltaT=diff(T)                      % Calculamos el cambio de temperatura
DeltaV=diff(V)                      % Calculamos el cambio de volumen molar durante la transformacion de fases
DeltaS=diff(S)                      % Calculamos el cambio de entropía molar durante la transformacion de fases
DeltaH=diff(H)
% Usamos la ecuación de Clasius-Clapeyron para describir mejor el efecto de
% la temperatura sobre el cambio de las propiedades del ELV, sin embargo el
% valor hallado será una aproximación al valor real, puesto que tanto el
% cambio entálpico como el de volumen molar varían en magnitud entre 100oC y
% 300oC
Pf=Po.*exp(-DeltaH./Rene*(1/T(2)-1/T(1))) % Presión en bar
PfmH2O=Pf/1.01325*10               % Presion equivalente a metros de agua
% La presión requerida para el agua se evapore a 300oC es de
% aproximadamente 98 bar lo que correspondería a una profundidad aproximada
% de 963m ~ 1Km

T =

   1.0e+02 *

   3.731500000000000   5.731500000000000


DeltaT =

   200


DeltaV =

  30.077226000000000


DeltaS =

     1.088460000000000e+02


DeltaH =

     4.061574000000000e+04


Pf =

  97.665365699173776


PfmH2O =

     9.638822176084261e+02

http://biblioteca.ucm.es/media/images/blogs/fotoblog4603.JPG
Imagen tomada desde: http://biblioteca.ucm.es/blogs/GeoBlog/4603.php#.WbcVLtGQzDc
Consulte el mismo link para mayor información


Published with MATLAB® R2012b