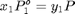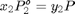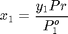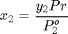Segunda Evaluación Parcial Semestre U-2017

Curso de Pre-grado: Fisicoquímica para Ingenieros

Contents

Primer Problema

(7 puntos) La tabla 1 muestra las propiedades físicas y los datos de solubilidad de algunos gases de importancia industrial. En la figura 1 se muestra un sistema típico de absorción de gas. El gas se hace burbujear en contracorriente con agua en una columna de lecho empacado y luego el líquido se lleva a un tanque de almacenamiento para su posterior uso. Se asume generalmente, que la columna opera a temperatura y presión constante, y que las corrientes de salida de la columna se encuentran en condiciones de equilibrio termodinámico. De acuerdo a su número de lista, determine para el gas correspondiente lo siguiente:

  1. Número de moles de gas absorbido por centímetro cúbico de agua a 30oC y 15oC cuando el gas ejerce una presión de 1 atm. Use la ley de Henry definida en la ecuación (1)
  2. Flujo mínimo de gas en mol h y m3/h (medidos a condiciones estándar de 273:15 K y 1 atm) que debe hacerse burbujear para saturar con el gas, una corriente de agua de 1 mh3 a 15oC cuando el gas ejerce una presión de 1 atm
  3. Ocurre un ascenso de la temperatura ambiental de 15oC a 30oC. En caso de que el gas se desorba con el cambio de temperatura, determine el porcentaje de desorción, y el volumen de gas desorbido (medido a la temperatura ambiente y 1 atm). Discuta sobre los riesgos de tal situación.

Sander R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmospheric Chemistry and Physics. 2015 apr;15(8):4399–4981. Available from: http://www.atmos-chem-phys.net/15/4399/2015/.

clear all
clc
close all
H298=55.3/56;                    % Constante de Henry a 298.15 K en atm
DeltaHR=4100;                  % Relación entre calor de dilución y R
PM=17.0305;                     % Peso Molecular del amoníaco
Ta=[15 30]+273.15;               % Temperatura en K
PNH3=1;                         % Presión en atm
Caudal=1*1E6;                   % Caudal de agua en cm3/h

Variación de Ley de Henry con la temperatura

Usamos la expresión del tipo van't Hoff que nos permite estimar la variación de la constante de Henry con cambios de temperatura, en intervalos pequeños donde puede considerarse que el calor de dilución del gas se mantiene aproximadamente constante

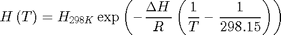
$$ H\left(T\right)=H_{298K}\exp\left(-\frac{\Delta H}{R}\left(\frac{1}{T}-\frac{1}{298.15}\right)\right) $$

Definimos la función en términos de la temperatura

H=@(T) H298.*exp(-DeltaHR*(1./T-1./298.15));

Determinamos el valor de la constante de Henry a 15^oC y 30^oC:

HT=H(Ta)

HT =

   0.612741744393877   1.238908611201399

Observamos que tal como se espera, el aumento de la temperatura conduce a un aumento de la constante de Henry, ya que la solubilidad del amoníaco gaseoso en agua, disminuye con aumentos de temperatura

Determinación del coeficiente de Bunsen

Se estima ahora el valor del coeficiente de Bunsen como una función de la constante de Henry

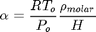
$$ \alpha=\frac{RT_o}{P_o}\frac{\rho_{molar}}{H} $$

R=83.14/1.01325;                % cm3*atm/mol/K
To=273.15;                      % K
Po=1;                           % bar
DensidadMolarSte=1/18.07;       % mol/cm3
alfa=R.*To./Po.*DensidadMolarSte./HT    % cm3 gas a STP / cm3 agua/atm

alfa =

   1.0e+03 *

   2.024225965565892   1.001145474310208

Número de moles de gas absorbidos a Ta

Para estimar el número de moles de gas absorbido por centímetro cúbico de agua a 30oC y 15oC cuando el gas ejerce una presión de 1 atm, sencillamente usamos la definición del coeficiente de Bunsen:

$$ n_{NH3}=\alpha\frac{p_{NH3}}{\frac{RT_o}{P_o}} $$

nNH3=alfa.*PNH3./(R.*To./Po)    % moles de gas por cm3 de agua

nNH3 =

   0.090315934268310   0.044668624150140

Observamos que a mayor temperatura, menor el número de moles de gas que pueden disolverse por unidad de volumen del solvente

Flujo de gas necesario para saturar Caudal de Agua a Ta

Usamos el caudal de agua para estimar el flujo mínimo de gas en mol h y m3/h (medidos a condiciones estándar de 273:15 K y 1 atm) que debe hacerse burbujear para saturar con el gas, una corriente de agua de 1 mh3 a 15oC cuando el gas ejerce una presión de 1 atm

Flujomolar=nNH3.*Caudal % mol/h
Flujovolumetrico= Flujomolar.*R.*To./Po /1E6 %m3/h

Flujomolar =

   1.0e+04 *

   9.031593426831041   4.466862415014006


Flujovolumetrico =

   1.0e+03 *

   2.024225965565892   1.001145474310208

Desorción del gas

Para estimar los moles desorbidos, sencillamente comparamos el estado final (2) con el estado inicial (1) y hallamos el porcentaje de desorción:

molesdesorbidos=(nNH3(2)-nNH3(1)).*Caudal % moles desorbidos por hora
volumengasdesorbido=molesdesorbidos.*R.*Ta(2)./Po./1000 % litros de gas desorbidos medidos a 30oC y 1 atm
DesorcionPorcentual=(nNH3(2)-nNH3(1))./nNH3(1).*100

molesdesorbidos =

    -4.564731011817034e+04


volumengasdesorbido =

    -1.135445180026215e+06


DesorcionPorcentual =

 -50.541812458653638

Segundo Problema

(6 puntos) El diclorobenceno (C6H4Cl2) puede existir en sus formas isoméricas como orto-, meta- y para-diclorobenceno, comúnmente llamadas o-DCB, m-DCB y p-DCB. El o-DCB o es usado como solvente y desodorizante, el m-DCB no tiene usos conocidos, y el p-DCB es usado en desodorizantes y pesticidas [1], también para repeler culebras, ratas, murciélagos e insectos [2]. Luego de la síntesis del DCB, el p-DCB puede separarse por filtración porque es sólido a condiciones atmosféricas, pero los otros dos isómeros son líquidos, y sólo elo-DCB es de importancia comercial [1]. En la figura ?? se muestran las fórmulas estructurales de los DCB’s [3] En la tabla se muestran las propiedades físicas más relevantes (incluídas las constantes de Antoine para estimar la presión de vapor con la ecuación (1) con P en mmHg y T en oC) del o-DCB y m-DCB [4][5][6][7]. Use esta información y sus conocimientos sobre la termodinámica del equilibrio de fases líquido y vapor para determinar lo siguiente: 1. Composición máxima en o-DCB y m-DCB que puede obtenerse por destilación de una mezcla con relación molar de 3 1 de o-DCB y m-DCB a la temperatura de 100oC 2. Eficiencia de la separación por destilación, cuando se vaporiza súbitamente una mezcla con relación molar de 3 1 de o-DCB y m-DCB a la presión promedio entre el punto de burbuja y el punto de rocío a la temperatura de 100oC 3. Factibilidad de separación de ambos compuestos por destilación súbita o flash a la presión promedio entre el punto de burbuja y el punto de rocío a la temperatura de 100oC

Preparación e Introducción de datos

clear all
clc
close all
PM=[147.002 147.002];
densidad20=[1.2884 1.3059 ];
factoracentrico=[0.324 0.324];
momentodipolar=[1.48 2.54 ];
Tfo=[248.39 256.0 ];
Tbo=[446.2 453.7];
Top=100;
% Presión de vapor según modelo de Antoine
A=[7.3037 7.07030];
B=[1782.4 1649.55];
C=[230.01 213.32];
P1=@(T) 10.^(A(1)-B(1)./(T+C(1)));
P2=@(T) 10.^(A(2)-B(2)./(T+C(2)));
% Composición de la solución a separar
z=[1 3]./4
% Variables globales
global z
global P
global P1vap
global P2vap

z =

   0.250000000000000   0.750000000000000

Warning: The value of local variables may have been changed to
match the
         globals.  Future versions of MATLAB will require that
         you declare
         a variable to be global before you use that variable.

Estudio de la Volatilidad Relativa

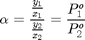
$$ \alpha=\frac{\frac{y_1}{x_1}}{\frac{y_2}{x_2}}=\frac{P_1^o}{P_2^o} $$

T=[20:1:Tbo(2)-273.15];
alfa=@(T) P1(T)./P2(T);
figure
subplot(1,2,1)
plot(T,alfa(T))
grid on
xlabel ('T(^oC)')
ylabel ('\alpha')
title ('\alpha para el sistema m-DCB(1)/o-DCB(2)')
subplot(1,2,2)
plot(1./(T+273.15),log10(P1(T)),'b',1./(T+273.15),log10(P2(T)),'r')
grid on
xlabel ('1/T(K)')
ylabel ('log_1_0 P_i ^o')
title ('P_i^o de m-DCB(1)/o-DCB(2)')
legend({'m-DCB','o-DCB'})
Top
alfaTop=alfa(Top)

Top =

   100


alfaTop =

   1.250537890852150

Modelo descriptivo para el ELV

Una solución de composición %25 molar de m-DCB en o-DCB se encuentra a la temperatura de 256 K lejos del punto crítico de los compuestos, por lo que puede modelarse usando la ecuación de gas ideal para la fase vapor. Dada la similitud en forma, tamaño y polaridad de estos isomeros podemos usar la ecuación de Raoult para la fase líquida. Para cada compuesto debe cumplirse entonces al ELV que:

  1. $$ x_1P^o_1=y_1P $$
  2. $$ x_2P^o_2=y_2P $$

Diagramas de equilibrio de fases

figure
y=@(x1) alfaTop.*x1./(1+(alfaTop-1).*x1);
x1=[0:0.01:1];
plot(x1,x1,x1,y(x1))
xlabel('x_1')
ylabel('y_1')
grid on

Presión de burbuja (Pb)

En el punto de burbuja la composición del líquido no difiere de aquella de la solución original

x=z;
Pb=x(1)*P1(Top)+x(2)*P2(Top)
yb=[x(1)*P1(Top)/Pb x(2)*P2(Top)/Pb]

Pb =

  67.910760250212292


yb =

   0.294206974026396   0.705793025973604

La máxima concentración del compuesto más volátil

La presión de burbuja es de 67.9108 mmHg y la primera burbuja de vapor por expansión isotérmica tiene una composición molar de m-DCB de 29.42% (máxima posible para este compuesto). Debemos recordar que la composición en la alimentación era de 25% en m-DCB.

Presión de rocío (Pr)

En el punto de rocío, la composición del vapor no difiere de aquella de la solución original, y la composición del líquido es desconocida

y=z;
  1. $$ x_1=\frac{y_1Pr}{P^o_1} $$
  2. $$ x_2=\frac{y_2Pr}{P^o_2} $$

Uniendo las ecuaciones 1 y 2 debe cumplirse que:

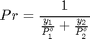
$$ Pr=\frac{1}{\frac{y_1}{P^o_1}+\frac{y_2}{P^o_2}} $$

Pr=1./sum(y(1)./P1(Top)+y(2)./P2(Top))

Pr =

  67.277588302072616


xr=[y(1)./P1(Top) y(2)./P2(Top)]*Pr

xr =

   0.210454819964769   0.789545180035231

La presión de rocio es 67.278 mmHg y la última gota de líquido (durante expansión isotérmica) tiene una composición de 21.04% m-DCB, o sea 78.96 % molar en o-DCB (máxima posible para este compuesto). Debemos recordar que la composición inicial de la solución en o-DCB era de 75% molar

Destilación Flash a Tmax

P=(Pb+Pr)/2      % Presión de operación
P1vap=P1(Top)
P2vap=P2(Top)

P =

  67.594174276142454


P1vap =

  79.919277108188012


P2vap =

  63.907921297553727

En este caso deben satisfacerse las ecuaciones del balance de masa y del equilibrio líquido-vapor:

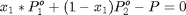  1. $$ x_1*P^o_1+(1-x_1)P^o_2 -P =0$$
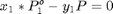
  2. $$ x_1*P^o_1-y_1P=0 $$
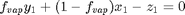
  3. $$ f_{vap}y_1+(1-f_{vap})x_1-z_1=0 $$

Se tienen tres ecuaciones con tres incógnitas: x_1, y_1, fvap Creamos un archivo auxiliar llamado ELVDCBs.m Este archivo DEBE ESTAR GUARDADO en la misma carpeta de trabajo donde se encuentre el archivo de este problema

Resolución del sistema de ecuaciones

Usamos la función fsolve de MatLab y usamos un vector de condiciones iniciales.

soluciones=fsolve(@ELVDCBs,[0.1 0.8 0.1])
%
% # x_1=soluciones(1)=0.230227409982384     % Fracción molar de m-DCB en líquido
% # y_1=soluciones(2)=0.272207011526092     % Fracción molar de m-DCB en vapor
% # f=soluciones(3)=  0.471004693206632     % Fracción de vaporización
%

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




soluciones =

   0.230227409982384   0.272207011526092   0.471004693206632

A 100^oC y una presión de 67.594 mmHg, la composición molar % en m-DCB en la fase líquida es de 23.02%, mientras que la del vapor es 27.55%, lográndose una vaporización del 47%. Al estimar la eficiencia de separación del m-DCB en el destilado obtenemos un valor de 51.28%, mientras que la eficiencia de separación del o-DCB es de 54.29%.

xfondo=[soluciones(1) 1-soluciones(1)];
ydestilado=[soluciones(2) 1-soluciones(2)];
fvap=soluciones(3);
eficienciamDCB=ydestilado(1)*fvap/z(1)*100
eficienciaoDCB=xfondo(2)*(1-fvap)/z(2)*100

eficienciamDCB =

  51.284311981016394


eficienciaoDCB =

  54.294144988999214

Conclusión: Debido a la baja eficiencia de separación de los compuestos (volatilidad relativa de 1.25 a las condiciones de operación del destilador flash), no se considera factible la operación. Se sugiere probar otros procesos de separación, tales como la extracción líquido-líquido

Tercer Problema

(6 puntos) Estime la eficiencia de separación del isopropanol presente en una solución de composición 40 % molar de isopropanol en agua y la composición del destilado y el producto de fondo obtenidos, cuando la solución se somete a una destilación flash a la temperatura promedio entre su punto de burbuja y su punto de rocío a la presión de 1 atm. Puede realizar el problema de forma gráfica o analítica según sea su preferencia. En caso de existir un azeotropo, estime la temperatura y composición de éste. (1 punto adicional)

Preparación e Introducción de datos

clear all
clc
close all
global P;
global Tflash;
global k;
global A;
global B;
global C;
global z;
global xx;
global yy;
global fvap;
global Ren;
%Ren=1.987; % cal/mol/K
Ren=1.986; % cal/mol
% Modelo de Antoine con p en bar y T en K
A=[4.8610 4.6543]
B=[1357.427 1435.264]
C=[-75.814 -64.848]
k=[659.5473 1230.2080 76.92 18.07]; % cal/mol
P=1.01325; % bar
z=[0.4 0.6]; % fracción molar de la alimentación

A =

   4.861000000000000   4.654300000000000


B =

   1.0e+03 *

   1.357427000000000   1.435264000000000


C =

 -75.813999999999993 -64.847999999999999

Temperatura de Burbuja

Seleccionamos el modelo de Wilson para describir los coeficientes de actividad de las especies en solución

xx=z;
Tb=fsolve(@WilsonELV2examen, 81+273.15)
TbC=Tb-273.15

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




Tb =

     3.543231057823244e+02


TbC =

  81.173105782324456

Función a resolver

function f=WilsonELV2examen(T) %x: Temperatura en grados K %k=[lambda12-lambda11 lamba21-lambda22 v1L v2L]; global P; global k; global A; global B; global C; global xx; global Ren; %Ren=1.987; % cal/mol/K Lambda12=k(4)./k(3).*exp(-k(1)./(Ren.*T)); %(T+273.15))); Lambda21=k(3)./k(4).*exp(-k(2)./(Ren.*T)); %(T+273.15))); gamma(1)=exp(-log(xx(1)+Lambda12.*xx(2))+xx(2).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2)))); gamma(2)=exp(-log(xx(2)+Lambda21.*xx(1))-xx(1).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2)))); f=xx(1).*gamma(1).*10.^(A(1)-B(1)./(T+C(1)))+xx(2).*gamma(2).*10.^(A(2)-B(2)./(T+C(2)))-P;

La temperatura de burbuja de la solución 40% molar en isopropanol es 81.17 ^oC

Temperatura de Rocío

yy=z;
solucion=fsolve(@WilsonELV2examen2,[85+273.15 0.05])
Tr=solucion(1)
xr=solucion(2)
TrC=Tr-273.15
xr=xx
% La temperatura de rocío es de  87.29 ^oC y la última gota de líquido
% tiene una fracción molar de 0.0486 en isopropanol

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




solucion =

   1.0e+02 *

   3.604454427694403   0.000486442168075


Tr =

     3.604454427694403e+02


xr =

   0.048644216807500


TrC =

  87.295442769440342


xr =

   0.048644231708661   0.951355768291339

Función a resolver:

function f=WilsonELV2examen2(w)

x: Temperatura en grados K

k=[lambda12-lambda11 lamba21-lambda22 v1L v2L];

global P; global k; global A; global B; global C; global xx; global yy; global Ren; %Ren=1.987; % cal/mol/K T=w(1);% xx(1)=w(2);% xx(2)=1-xx(1);

Lambda12=k(4)./k(3).*exp(-k(1)./(Ren.*T)); %(T+273.15)));

Lambda21=k(3)./k(4).*exp(-k(2)./(Ren.*T)); %(T+273.15)));

gamma(1)=exp(-log(xx(1)+Lambda12.*xx(2))+xx(2).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2))));

gamma(2)=exp(-log(xx(2)+Lambda21.*xx(1))-xx(1).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2))));

f(1)=yy(1).*P./(gamma(1).*10.^(A(1)-B(1)./(T+C(1))))+yy(2).*P./(gamma(2).*10.^(A(2)-B(2)./(T+C(2))))-1;

f(2)=xx(1)*gamma(1).*10.^(A(1)-B(1)./(T+C(1)))-yy(1);

Destilación Flash a T promedio entre Tburbuja y Trocío

Tflash=mean([Tb,Tr])
flash=fsolve(@WilsonELV2examen3,[0.1 0.5 0.5])
xsalida=[flash(1) 1-flash(1)]
ysalida=[flash(2) 1-flash(2)]
fvaporizacion=fvap
eficiencia=ysalida(1).*fvaporizacion./z(1).*100

Tflash =

     3.573842742758824e+02


Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




flash =

   0.111045960990455   0.484555361493657   0.773619108364641


xsalida =

   0.111045960990455   0.888954039009545


ysalida =

   0.484555361493657   0.515444638506343


fvaporizacion =

   0.773619123265802


eficiencia =

  93.715323483116734

El producto de fondo tiene una fracción molar en isopropanol de 0.11884; mientras que el destilado tiene una fracción molar en isopropanol de 0.4846 y a la temperatura promedio entre el punto de burbuja y el de rocío se vaporiza el 76,9% de la alimentación; lo que permite separar el 93.13% del isopropanol presente en la alimentación.

Función a resolver

function f=WilsonELV2examen3(w)

x: Temperatura en grados K

k=[lambda12-lambda11 lamba21-lambda22 v1L v2L];

global P; % global Tflash; global k; global A; global B; global C; global z; global xx; global yy; global fvap; global Ren;

Ren=1.987; % cal/mol/K

Vector de incógnitas

T=Tflash;xx(1)=w(1); % Composición del líquido yy(1)=w(2); % Composición del vapor fvap=w(3); % Fracción de vaporización

Lambda12=k(4)./k(3).*exp(-k(1)./(Ren.*T));

Lambda21=k(3)./k(4).*exp(-k(2)./(Ren.*T));

gamma(1)=exp(-log(xx(1)+Lambda12.*xx(2))+xx(2).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2))));

gamma(2)=exp(-log(xx(2)+Lambda21.*xx(1))-xx(1).*(Lambda12./(xx(1)+Lambda12.*xx(2))-Lambda21./(Lambda21.*xx(1)+xx(2))));

f(1)=xx(1).*gamma(1).*10.^(A(1)-B(1)./(T+C(1)))+xx(2).*gamma(2).*10.^(A(2)-B(2)./(T+C(2)))-P;

f(2)=xx(1)*gamma(1).*10.^(A(1)-B(1)./(T+C(1)))-yy(1);

f(3)=yy(1)+(1-fvap)./fvap.*xx(1)-z(1)./fvap;

Estimación del punto azeotrópico

En el punto azeotrópico se cumple que:

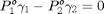
$$ P_1^o\gamma_1-P_2^o\gamma_2=0 $$

$$ P-x_1P_1^o\gamma_1-x_2P_2^o\gamma_2=0 $$

Resolvemos la función:

Azeotropo=fsolve(@WilsonELV2Azeotropo, [0.5 75+273.15])

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.




Azeotropo =

   1.0e+02 *

   0.007033442839133   3.533338220890834


Published with MATLAB® R2012b