Equilibrio Líquido-Vapor en sistemas no ideales: aplicaciones

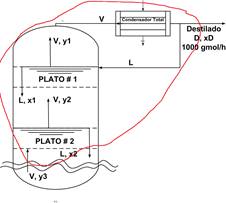
En la figura se muestra el esquema de operación del tope de una torre de destilación. La torre opera a presión atmosférica y permite separar la mezcla acetona-agua. Todas las variables x y y se refieren a la fracción molar del compuesto más volátil en las corrientes. L y V representan los flujos molares de líquido y vapor.

1.     Determine todas las composiciones y flujos molares de las corrientes mostradas, así como las temperaturas de operación, si se sabe que: La relación L/V es constante e igual a 1/8. El destilado tiene una composición xD=0.8 molar en A

2.     Ubique gráficamente todas las composiciones de las corrientes en los diagramas de equilibrio del sistema.

Contenido

§  Preparación e introducción de datos

§  Estudio del equilibrio líquido-vapor del sistema acetona(1)-agua(2) a P=1 atm

§  Estudio de la existencia de punto azeotrópico

§  Balance de masa global

§  Balance de masa por componente en envolvente indicada

§  Condensador Total:

§  Plato 1

§  Plato 2

§  Plato 3

§  Representación gráfica de los resultados

§  Perfil de Temperatura

Preparación e introducción de datos

clear all                           % Borramos toda posible variable
clc                                 % Limpiamos la pantalla de comando
close all                           % Cerramos toda ventana de figura
% Creamos variables globales
global y                            % Composición en fracción molar del vapor
global x                            % Composición en fracción molar del líquido
global k                            % Constantes del modelo de G^E a usar
global A                            % Constantes de Antoine para Pi^o
global B
global C
global Ren                          % Constante de los gases
global P                            % Presión de operación de la torre en bar
P= 1.01325;
Ren=1.986;                          % R en cal/mol para constantes del modelo de Wilson
% Acetona: Compuesto 1 (más volátil)  Agua: Compuesto 2 ( más pesado)
% Perry, Robert "Manual del ingeniero químico" tomo
k=[344.3346 1482.2133 74.05 18.07];  % Modelo de Wilson
% Constantes de Antoine con P en bar y T en K
% http://webbook.nist.gov/cgi/cbook.cgi?ID=C67641&Mask=4#Thermo-Phase
A=[4.42448 4.6543];
B=[1312.253 1435.234];
C=[-32.445 -64.848];
Rint=1/8;                           % Relación de reflujo interno L/V
xD=[0.8 0.2];                       % Composición molar del destilado
D=1000;                             % Flujo molar del destilado en gmol/h

Estudio del equilibrio líquido-vapor del sistema acetona(1)-agua(2) a P=1 atm

Antes de estudiar el funcionamiento de la torre debemos conocer que tipo de desviaciones de la idealidad presenta el sistema, para lo cual podemos realizar los diagramas de fase correspondientes. Iniciamos estimando la temperatura de burbuja de una serie de soluciones desde 0% a 100 % acetona en agua usando el archivo de función TburbujaWilson.m

xx=[0:0.005:1]';
Tb0=100+273.15;
yc=[];
for i=1:max(size(xx))
    x=[xx(i) 1-xx(i)];
    options=optimset('Display','off');
    Tb(i)=fsolve(@Tburbuja2Wilson, Tb0, options);
    Tb0=Tb(i);
    yc=[yc;y];
end
Tb=Tb';
figure
subplot(1,2,1)
plot(xx(:,1),Tb, yc(:,1), Tb,'LineWidth',2)
grid on
xlabel ('(x,y): fracción molar de acetona')
ylabel ('Temperatura (K)')
axis([0 1 50+273.15 100+273.15])
subplot(1,2,2)
plot(xx(:,1),xx(:,1), xx(:,1),yc(:,1),'LineWidth',2)
axis([0 1 0 1])
grid on
xlabel ('x:fracción molar de acetona en fase líquida')
ylabel ('y:fracción molar de acetona en fase vapor')

Estudio de la existencia de punto azeotrópico

Estimamos la constante de reparto K=y/x para cada compuesto

K=yc./[xx 1-xx];
VolatilidadRelativa=K(:,1)./K(:,2);
figure
plot(xx, VolatilidadRelativa, 'LineWidth',2)
xlabel('Fracción molar en acetona(1) en fase líquida')
ylabel('Volatilidad Relativa: \alpha=K_1/K_2')
grid on

La figura anterior indica que no existe punto azeotrópico, ya que para ninguna composición se cumple que la volatilidad relativa sea igual a uno

Balance de masa global

$$ V=L+D = V Rint+D \rightarrow V=\frac{D}{1-Rint} $$

Usamos la relación de reflujo externo y el flujo molar de destilado para determinar la magnitud de los flujos molares de la zona de enriquecimiento (ZE)

V=D/(1-Rint)                        % Flujo molar de vapor en ZE
L=V-D                               % Flujo molar de líquido en ZE
 
V =
 
     1.142857142857143e+03
 
 
L =
 
     1.428571428571429e+02
 

Balance de masa por componente en envolvente indicada

Recordemos que todas las corrientes tendrán una composición indicada por un vector cuya primera componente coincide con la fracción molar del más volátil, y la segunda componente coincide con la fracción molar del más pesado. El subíndice que acompaña a y y x identifica la etapa o plato dentro de la torre de destilación $$ y_{i+1}V=Lx_{i}+Dx_D $$

A partir de este balance se determina la ecuación de la línea de operación de la zona de enriquecimiento $$ y_{i+1}=\frac{L}{V}x_{i}+\frac{D}{V}x_D $$

Condensador Total:

La condensación total del vapor V de composición y_1 garantiza que x_D=y_1=0.8, por lo que se conoce de manera directa, la composición molar del vapor que sale del plato 1

y1=xD;

Plato 1

El vapor V de composición y_1 está en equilibrio termodinámico (ELV) con el líquido que sale del plato. Para ello debe cumplirse para cada uno de los componentes que: $$ y_1P=x_1P_{vap}\gamma $$

Se tiene un sistema de dos ecuaciones con dos incógnitas: la temperatura del ELV, y la composición de la fase líquida. Resolvemos el sistema usando un archivo auxiliar de función ELV2Wilson.m

y=y1;
Plato1=fsolve(@ELV2Wilson, [65+273.15 0.2])
x1=[Plato1(2) 1-Plato1(2)]      % Fracción molar del líquido a la salida del plato 1
T1=Plato1(1)-273.15             % Temperatura del ELV en el plato 1
 
Equation solved.
 
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
 
 
 
 
Plato1 =
 
   1.0e+02 *
 
   3.357419182982953   0.002632995717102
 
 
x1 =
 
   0.263299571710198   0.736700428289802
 
 
T1 =
 
  62.591918298295298
 

Plato 2

Usamos la línea de operación para hallar la composición del flujo de vapor que sale de plato 2

y2=Rint.*x1+D./V.*xD
% Ahora estimamos la composición del líquido en ELV con este vapor:
y=y2;
Plato2=fsolve(@ELV2Wilson, [70+273.15 0.2])
x2=[Plato2(2) 1-Plato2(2)]      % Fracción molar del líquido a la salida del plato 1
T2=Plato2(1)-273.15             % Temperatura del ELV en el plato 1
 
y2 =
 
   0.732912446463775   0.267087553536225
 
 
Equation solved.
 
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
 
 
 
 
Plato2 =
 
   1.0e+02 *
 
   3.412062639336341   0.001030019881065
 
 
x2 =
 
   0.103001988106462   0.896998011893538
 
 
T2 =
 
  68.056263933634057
 

Plato 3

Usamos la línea de operación para hallar la composición del flujo de vapor que sale de plato 3

y3=Rint.*x2+D./V.*xD
% Ahora estimamos la composición del líquido en ELV con este vapor:
y=y3;
Plato3=fsolve(@ELV2Wilson, [80+273.15 0.1]);
x3=[Plato3(2) 1-Plato3(2)]    % Fracción molar del líquido a la salida del plato 1
T3=Plato3(1)-273.15           % Temperatura del ELV en el plato 1
 
y3 =
 
   0.712875248513308   0.287124751486692
 
 
Equation solved.
 
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
 
 
 
 
x3 =
 
   0.086365103036454   0.913634896963546
 
 
T3 =
 
  69.568270459423388
 

Representación gráfica de los resultados

figure
plot(xx(:,1),xx(:,1), xx(:,1),yc(:,1),'LineWidth',2)
axis([0 1 0 1])
grid on
xlabel ('x:fracción molar de acetona en fase líquida')
ylabel ('y:fracción molar de acetona en fase vapor')
hold on
% Línea de operación
yLOP=Rint.*xx(:,1)+D./V.*xD(1,1);
plot(xx(:,1),yLOP,'-k', 'LineWidth',2)
text(0.85,0.83, 'LOP')
hold on
xplatos=[x1;x2; x3];
yplatos=[y1; y2; y3];
Tplatos=[T1;T2;T3];
line([yplatos(1,1) xplatos(1, 1)],[yplatos(1,1) yplatos(1,1)], 'LineWidth',2, 'Color', 'red')
text(yplatos(1, 1)*0.8,yplatos(1, 1)*1.05, 'Cond. Total')
hold on
for j=2:3
    line([xplatos(j-1,1) xplatos(j, 1)],[yplatos(j,1) yplatos(j,1)], 'LineWidth',2, 'Color', 'red')
    hold on
    line([xplatos(j-1,1) xplatos(j-1, 1)],[yplatos(j-1,1) yplatos(j,1)],'LineWidth',2, 'Color', 'blue')
    hold on
    text(xplatos(j-1,1)*1.1,yplatos(j-1,1)*0.95,['Plato_' num2str(j-1)])
    hold on
end

Perfil de Temperatura

figure
plot(1:3,Tplatos,'*-','LineWidth',2)
grid on
xlabel('Plato')
ylabel('T(^oC)')


Published with MATLAB® R2012b