Ajuste de modelos de energía libre de Gibbs de Exceso a datos de ELV

Sistema Acetona(1)-Cloroformo(2) a Presión constante http://www.ddbst.com/en/EED/VLE/VLE%20Acetone%3BChloroform.php Determine si el modelo de Wilson describe correctamente el ELV del sistema Acetona(1)-Cloroformo(2) a 1 atm Momento Dipolar a 20^oC: \mu_1=2.88D \mu_2=1.11D Peso Molecular: PM_1=58.080 PM_2=119.377 Volumen Molar a 20^oC: V_1^o=74.05 V_2^o=80.67 cm^3/mol Factor acéntrico: \omega_1=0.304 \omega_2=0.288 Datos desde: http://www.echeguru.com/html_data_files/Acentric_Factor_and_Dipole_Moment.html

Contents

Preparación

clear all
clc
close all
global Ren
global T
global Vo

Introducción de datos

P=760;               % torr
Ren=1.987;           % cal/mol/K
Vo=[74.05 80.67];  % cm^3/mol
% Primera columna: Temperatura en K
% Segunda columna: fracción molar en acetona en fase líquida
% Tercera columna: fracción molar en acetona en fase vapor
Txy=[
335.75 	0.09800 	0.06000
336.65 	0.18600 	0.14300
337.25 	0.26600 	0.23000
337.55 	0.36000 	0.36000
336.95 	0.46800 	0.51400
335.85 	0.57800 	0.64600
334.65 	0.67300 	0.75100
333.45 	0.75500 	0.83000
332.15 	0.82700 	0.89000
331.05 	0.89200 	0.93900
330.15 	0.94900 	0.97500];
x=Txy(2:end-1,2);
y=Txy(2:end-1,3);
T=Txy(2:end-1,1);
[x, indice]=sort(x);
y=y(indice);
T=T(indice);
% Creamos un arreglo de columnas para la composición del líquido
% La primera columna contiene la fracción molar en cloroformo, la segunda en
% agua. No tomamos ni la primera ni la última fila porque contienen la
% datos de los compuestos puros
x=[x 1-x];
y=[y 1-y];

Determinación de la presión de vapor de compuestos puros

Usando la ecuación de Antoine 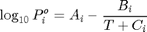$$ \log_{10}P_i^o=A_i-\frac{B_i}{T+C_i} $$ P en torr y T en ^oC

A=[7.11714 6.95465];
B=[1210.595 1170.966];
C=[229.664 226.232];
% Valores de Tabla 13-4 Manual del Ingeniero Químico Perry, R. 1996
P1vap=10.^(A(1)-B(1)./((T-273.15)+C(1))); % mmHg
P2vap=10.^(A(2)-B(2)./((T-273.15)+C(2))); % mmHg

Determinación de los coeficientes de actividad

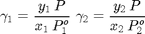
$$ \gamma_1=\frac{y_1\:P}{x_1\:P_1^o} $$ $$ \gamma_2=\frac{y_2\:P}{x_2\:P_2^o} $$

Para todos los cálculos usamos los operadores precedidos de punto ya que necesitamos operaciones elemento a elemento

gamma1=y(:,1).*P./(P1vap.*x(:,1));
gamma2=y(:,2).*P./(P2vap.*x(:,2));

Representación gráfica de resultados

figure
plot(x(:,1), gamma1, '+-b', x(:,1), gamma2, '*-r')
xlabel('Fracción molar en fase líquida x_1')
ylabel('\gamma_1 & \gamma_2')
title('ELV acetona(1)/cloroformo(2) a T=50^oC')
grid on
% El sistema presenta desviaciones negativas de la idealidad
% Para cada compuesto la fugacidad en solución es inferior a la que tendría
% en una solución ideal de la misma composición a la misma T y P

Determinación de la Energía Libre de Gibbs de Exceso

$$ \frac{G^E}{RT}=x_1\log \gamma_1+x_2\log \gamma_2 $$

GERT=x(:,1).*log(gamma1)+x(:,2).*log(gamma2);
% Las desviaciones de la idealidad son negativas y sugieren que no hay una
% influencia significativa de la forma y tamaño en las moléculas, puesto que
% la parábola G^E/RT es casi simétrica alrededor de su foco.
% Las desviaciones de la idealidad están causadas por una fuerte diferencia
% de polaridad entre las moléculas

Ajuste al modelo de Wilson

El modelo de Wilson posee dos parámetros de interacción y es no lineal:

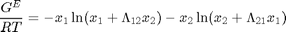
$$\frac{G^E}{RT}=-x_1\ln (x_1+\Lambda_{12}x_2)-x_2\ln (x_2+\Lambda_{21}x_1) $$

El ajuste requiere una regresión sobre una función no lineal que debe construirse en un archivo auxiliar que deberá llamarse GEWilson.m y estar guardado en la misma carpeta de trabajo que se usa Debe escribirse de esta forma:

Función no lineal sobre la que se efectuará la regresión

Transcriba esto en un archivo .m omitiendo el símbolo % function f=GEWilson(beta,x) % beta: parámetros del modelo de Wilson % siempre beta debe ser el primer argumento global Ren global T global Vo x1=x(:,1); x2=x(:,2); b1=Vo(2)./Vo(1).*exp(-beta(1)./(Ren.*T)); % beta(1) b2=Vo(1)./Vo(2).*exp(-beta(2)./(Ren.*T)); % beta(2); f=-x1.*log(x1+b1.*x2)-x2.*log(x2+b2.*x1);

X=x;
Y=GERT;
beta0=[100 -500]; % condiciones iniciales Tabla 13-2 Perry,1996
% La función nlinfit efectuará la regresión no lineal guardando los valores
% óptimos para las constantes de Wilson en el vector beta
[beta,R,J,CovB,MSE,stats]= nlinfit(X,Y,@GEWilson,beta0)
% Una vez que se obtienen los valores de beta que minimizan el error de
% regresión, los usamos para calcular el valor de GExceso/RT
Ycalc=GEWilson(beta,X);
% Esta rutina para la evaluación del ajuste escapa del objetivo del curso de
% Fisicoquímica. De estar interesado podemos conversar durante las horas de
% consulta
[rcuadrado,rcuadradoajustado,p, ErrorTotal]=BondadAjuste(X,Y,Ycalc,1)
% Los parámetros rcuadrado=0.998, rcuadradoajustado=0.9978, valor p <0.05 y
% la magnitud y patrón de los residuos, indican que el modelo representa
% adecuadamente los datos experimentales

beta =

   1.0e+02 *

   1.008120907945681  -4.828031960151259


R =

   0.001487324589539
   0.000029779242526
  -0.002754429656749
   0.000292274975425
   0.002257616879847
   0.000096849275280
  -0.002142207432440
   0.001450885387348
  -0.000552157860602


J =

   1.0e-03 *

   0.223543707225499   0.366912221015448
   0.286259897509841   0.444802130104553
   0.335446638278545   0.491139508908509
   0.360549719081866   0.495971467631179
   0.351757909053433   0.456317727409191
   0.316433309998618   0.391506663322103
   0.265396088310378   0.315889111051837
   0.205009131310729   0.236225377955322
   0.137848905738477   0.154408644301197


CovB =

   1.0e+02 *

   3.849542404481194  -2.803444235251314
  -2.803444235251314   2.064708075408912


MSE =

     3.141505969330311e-06


stats = 

              ErrorModel: 'constant'
         ErrorParameters: 0.001772429397559
           ErrorVariance: @(x)mse*ones(size(x,1),1)
                     MSE: 3.141505969330311e-06
          ScheffeSimPred: 3
          WeightFunction: 0
            FixedWeights: 0
    RobustWeightFunction: 0


nx =

     9


columnasx =

     2


ny =

     9


columnasy =

     1


Residuales =

   0.001487324589539
   0.000029779242526
  -0.002754429656749
   0.000292274975425
   0.002257616879847
   0.000096849275280
  -0.002142207432440
   0.001450885387348
  -0.000552157860602


ErrorTotal =

     2.199054178531218e-05


rcuadrado =

   0.998034368586514


F =

     3.554196647537416e+03

El modelo es significativo al 95% nivel de confianza con un valor p= 9.8067e-11

rcuadrado =

   0.998034368586514


rcuadradoajustado =

   0.997753564098873


p =

     9.806666589895485e-11


ErrorTotal =

     2.199054178531218e-05

Representación gráfica de resultados

figure
plot(x(:,1), GERT, '+k', x(:,1), Ycalc, 'r*-')
xlabel('Fracción molar en fase líquida x_1')
ylabel('GE/RT')
title('ELV acetona(1)/cloroformo(2) a P=1atm')
grid on
legend('Exp', 'Wilson')

Conclusión

El modelo de Wilson representa satisfactoriamente las relaciones descriptivas del equilibrio líquido-vapor del sistema acetona(1)-cloroformo(2) a 1 atm


Published with MATLAB® R2012b