Conceptos Geométricos

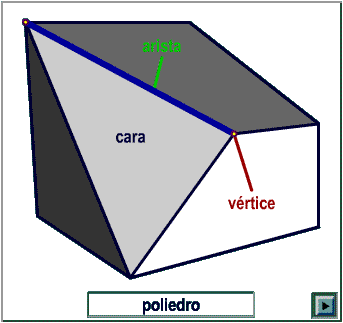
Poliedro

Sólido limitado por superficies planas (polígonos). Sus partes se denominan:

• caras: polígonos que limitan al poliedro,
• aristas: lados de las caras del poliedro,
• vértices: puntos donde concurren varias aristas.

Clasificación de los Poliedros

Los poliedros se clasifican básicamente en:

• poliedros regulares
• poliedros irregulares

Poliedro Regular

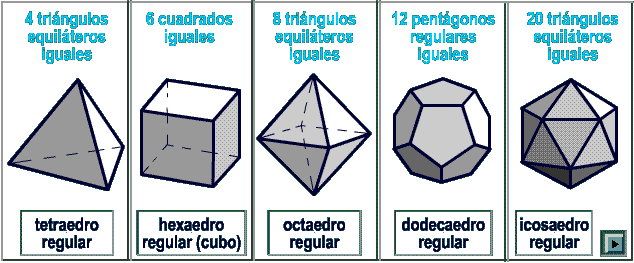
Poliedro cuyas caras son polígonos regulares iguales y todas sus aristas son de igual longitud; en consecuencia, todos sus vértices están contenidos en una esfera. Los poliedros regulares son cinco y se denominan:

• tetraedro regular: poliedro regular definido por 4 triángulos equiláteros iguales,
• hexaedro regular (cubo): poliedro regular definido por 6 cuadrados iguales,
• octaedro regular: poliedro regular definido por 8 triángulos equiláteros iguales,
• dodecaedro regular: poliedro regular definido por 12 pentágonos regulares iguales,
• icosaedro regular: poliedro regular definido por 20 triángulos equiláteros iguales.

poliedros regulares

Poliedro Irregular

Poliedro definido por polígonos que no son todos iguales.

Clasificación de los Poliedros Irregulares

Los poliedros irregulares se clasifican básicamente en:

• tetraedro, pentaedro, hexaedro, heptaedro, octaedro,
• pirámide
• prisma

denominación de los poliedros irregulares,
según el número de sus caras

Pirámide

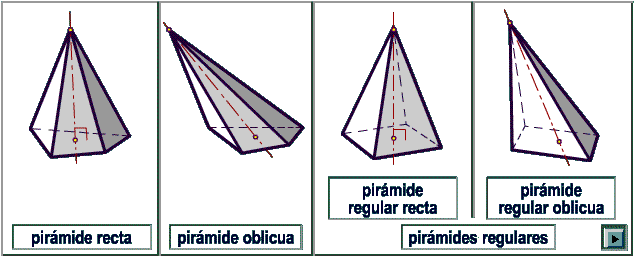
Poliedro definido por un polígono base y cuyas caras laterales son triángulos que poseen un vértice común (V), denominado vértice de la pirámide, que no está contenido en el plano base. La recta que pasa por el vértice de la pirámide y el centro geométrico de la base se denomina eje de la pirámide (e). Las pirámides se clasifican en:

• pirámide recta: el eje es perpendicular al polígono base,
• pirámide oblicua: el eje no es perpendicular al polígono base,
• pirámide regular: la base es un poligono regular,
  • pirámide regular recta: la base es un poligono regular y el eje es perpendicular al polígono base.
  • pirámide regular oblicua: la base es un poligono regular y el eje no es perpendicular al polígono base.

pirámides

Prisma

Poliedro definido por dos polígonos iguales y paralelos (bases) y cuyas caras laterales, en consecuencia, son paralelogramos. La recta que une los centros geométricos de las bases se denomina eje del prisma (e). Los prismas se clasifican en:

• prisma recto: el eje es perpendicular a los polígonos base,
• prisma oblicuo: el eje no es perpendicular a los polígonos base,
• prisma regular: las bases son poligonos regulares,
  • prisma regular recto: las bases son poligonos regulares y el eje es perpendicular a los polígonos base.
  • prisma regular oblicuo: las bases son poligonos regulares y el eje no es perpendicular a los polígonos base.
• paralelepipedo: prisma cuyas bases son paralelogramos. Pueden ser a su vez rectos u oblicuos

prismas

Conceptos Geométricos