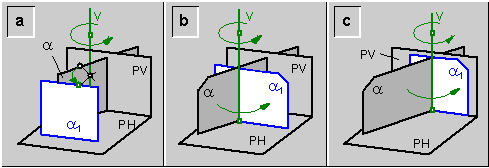
Para rotar un plano (a) que se encuentre en posición vertical hasta una posición frontal (a₁), debe hacerse girar el plano (a) a través de un eje vertical (v)\ fig.9a. El eje de rotación (v), puede también estar contenido en el plano (a)\ fig.9b, o ser la traza vertical del plano (a)\ fig.9c, en este caso se coloca el plano (a) sobre el plano vertical de proyección.

 

 

Al encontrarse el plano (a) en posición frontal (a₁), su proyección vertical se encuentra en verdadero tamaño.

 

 

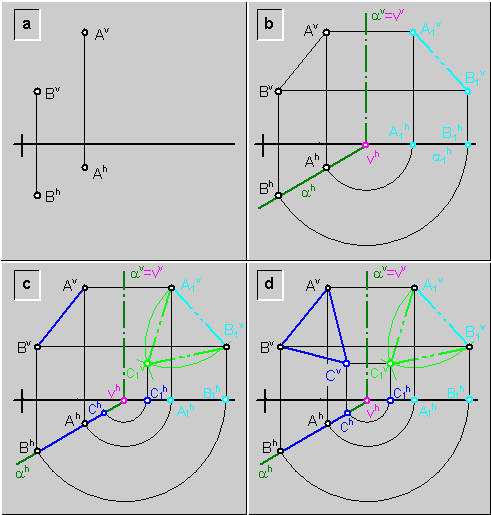
Ejemplo: Definir las proyecciones del triángulo equilátero (A;B;C) contenido en un plano vertical (a), conocido su lado (A-B) y dado que el vértice (C) esta por debajo de (B)\ fig.10a:

 

Solución:

 

a)     La proyección horizontal (A^h-B^h) del lado (A-B) define la proyección horizontal (a^h) de la traza horizontal del plano (a) que contiene al triángulo (A;B;C); y la proyección vertical (a^v) de la traza vertical del plano (a) es perpendicular a la línea de tierra y se corta con (a^h) en la línea de tierra, por lo tanto se definen ambas trazas\ fig.10b.

b)    Se elige como eje vertical (v) de rotación a la traza vertical del plano (a) y se rota, a través de él, el lado (A-B) hasta colocarlo sobre el plano vertical de proyección (A₁-B₁).

 

 

c)     Se dibuja, en verdadero tamaño, el triángulo (A; B; C) en su proyección vertical girada (A₁^v; B₁^v; C₁^v), y se define la proyección horizontal (C^h) del vértice (C), y por consiguiente la proyección horizontal (A^h; B^h; C^h) del triángulo (A; B; C)\ fig.10c.

d)    Se define la proyección vertical (C^v) del vértice (C), y por consiguiente la proyección vertical (A^v; B^v; C^v) del triángulo (A; B; C)\ fig.10d.

---