Campo de Direcciones
Consideremos la siguiente ecuación diferencial:
![]() (1)
(1)
| > | restart:with(DEtools): |
| > | ED1:=diff(y(x),x) = a+b*y(x); |
![]()
Antes de hacer cualquier representación gráfica es necesario espicificar los parámetros involucrados en la ecuación, en este caso
![]() y
y
![]() .
.
| > | a:=4: b:=1/8: |
| > | dfieldplot(ED1, y(x), x=0..10,y=0..100, title=`Ejemplo 1`,color=a+b*y,arrows=MEDIUM); |
![[Maple Plot]](images/campo_direcciones5.gif)
La ecuación (1) es una ecuación diferencial lineal de primer orden que tiene como sulución:
| > | ED1:=diff(y(x),x) = a+b*y(x);dsolve(ED1,y(x)); |
![]()
![]()
Esta curva se puede graficar directamente sobre el campo de direcciones para un conjunto particular de condiciones iniciales, en este caso, como la ecuación diferencial es de primer orden bastara una condición inicial y escojeremos que y(0) = 1.
| > | DEplot(ED1,y(x),x=0..10,[[y(0)=1]],y=0..100,title=`Solucion`,color=green,linecolor=-32+exp(1/8*x)); |
![[Maple Plot]](images/campo_direcciones8.gif)
La clase de ecuación diferencial como la que aparece en la ecuación (1) surge en la descripción de un objeto que cae en nuestra atmosfera. El movimiento de este objeto de masa
![]() estará gobernado por la segunda ley de Newton,
F =
estará gobernado por la segunda ley de Newton,
F =
![]() a.
Si se considera que el objeto cae sometido a la accion de la fuerza de la gravedad
a.
Si se considera que el objeto cae sometido a la accion de la fuerza de la gravedad
![]() y a la resistencia del aire, que supondremos proporcional a la velocidad:
y a la resistencia del aire, que supondremos proporcional a la velocidad:
![]() , entonces la segunda ley de Newton se puede escribir de la forma:
, entonces la segunda ley de Newton se puede escribir de la forma:
![]()
Supondremos que
![]() Kg,
Kg,
![]() Kg/s, y que el cuerpo parte del reposo, entonces
Kg/s, y que el cuerpo parte del reposo, entonces
![]()
| > | m:=8:kappa:=2: |
| > | ED2:=diff(v(t),t) = 9.8 - kappa/m*v(t); sol:=dsolve([ED2,v(0)=0],v(t)); |
![]()
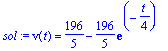
El gráfico de la solución es:
| > | DEplot(ED2,v(t),t=0..10,[[v(0)=0]],v=0..100,title=`Solucion particular`,color=green,linecolor=49-49*exp(-1/5*t)); |
![[Maple Plot]](images/campo_direcciones19.gif)
Es importante notar que cada segmento que aparece en la figura es en realidad una linea tangente al gráfico de la solución de la ecuación diferencial. Ahora grafiquemos unicamente el campo de direcciones
| > | dfieldplot(ED2, v(t), t=0..10,v=0..100, title=`Campo de Velocidades`,color=green,arrows=MEDIUM); |
![[Maple Plot]](images/campo_direcciones20.gif)
Se puede notar que existe un cierto
valor crítico
para la velocidad, que es aquel donde la velocidad de hace cero, y en la figura esta representada por las lineas de pendiente cero. Si hacemos
![]() , en la ecuación diferencial, lo que queda es despejar la velocidad:
, en la ecuación diferencial, lo que queda es despejar la velocidad:
| > | ec1:=subs(diff(v(t),t)=0,ED2); solve(ec1,v(t)); |
![]()
![]()
Es claro que la función
![]() (m/s) es una solución particular de la ecuación diferencial y como es constante se llama una solución de equilibrio, por el equilibrio entre la fuerza de la gravedad y la fricción.
(m/s) es una solución particular de la ecuación diferencial y como es constante se llama una solución de equilibrio, por el equilibrio entre la fuerza de la gravedad y la fricción.
Otra cosa que se puede notar es que si la velocidad está por debajo de este valor crítico, todos los segmentos tienen pendiente positiva, lo que significa que a medida que el cuerpo cae la velocidad va en aumento hasta alcanzar la velocidad crítica, por otro lado, si la velocidad está por arriba de este valor crítico todos los segmentos tienen pendiente negativa, lo que significa que la velocidad va disminuyendo a medida que pasa el tiempo para finalmente alcanzar la velocidad crítica.
Tambien podemos decir que todas las soluciones convergen a la solución de equilibrio a medida que el tiempo aumenta.
Para graficar esta solución particular pues lo unico que tenemos que hacer es repetir lo anterior pero con la condicion inicial
![]() :
:
| > | DEplot(ED2,v(t),t=0..10,[[v(0)=39.2]],v=30..50,title=`Velocidad Limite`,color=blue,linecolor=t); |
![[Maple Plot]](images/campo_direcciones26.gif)
Fin.