|
Topología asociada a una distancia
|
Muchos de los conceptos estudiados no dependen de la métrica. Para definir clausura, frontera, densidad,...etc sólo interviene el concepto de conjunto abierto. Estos son los llamados conceptos topológicos, pues no dependen directamente de la definición de la métrica.
Veamos como se define una topología sobre un conjunto
Si en un conjunto X tomamos una familia de subconjuntos τ , cuyos elementos satisfacen las tres condiciones de abierto .
|
El par ( X, τ ) se llama espacio topológico.
La familia de conjuntos τ , se llama una topología sobre X, y sus elementos, los conjuntos A i , se llaman los abiertos de la topología.
Ejemplos de Topologías o como entretenerse con un simple rectángulo
1. Topología caótica. Si X es un conjunto cualquiera y τ es la familia { X, Æ}, entonces τ es una topología ( el lector debe verificarlo) llamada la topología caótica.
2. Topología discreta. Si X es cualquier conjunto y τ es la familia (X), formada por todos los subconjuntos de X, entonces τ es una topología llamada la Topología Discreta.
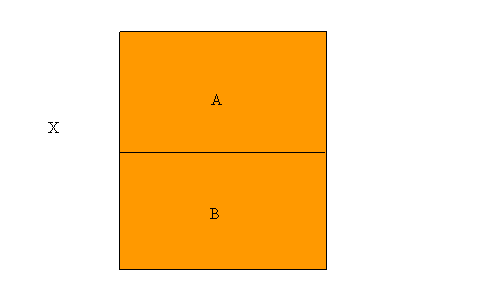
Veamos u ejemplo muy sencillo en el plano. Supóngase que X es el rectángulo de arriba U (un rectángulo del pleno formado por pares de números reales) el cual está dividido por dos rectángulos A y B , entonces τ = { X, Æ, A, B} es una topología sobre X ( verificarlo), la cual es discreta.
Podemos dividir el conjunto de arriba en cuatro rectángulos , para tener otro conjunto Y, y observar que está pasando con la topología.
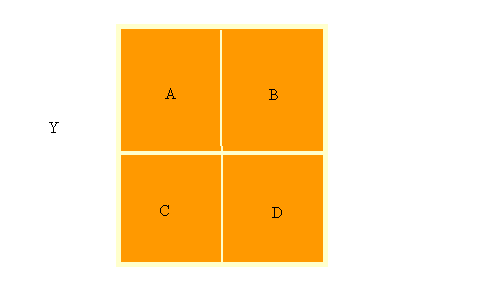
@¿Cómo definimos una topología en Y? Notemos que las partes de Y ( el número de subconjuntos de Y) consiste de 24 = 16 elementos. Una posible topología sería tomar τ ' = { X, Æ, A, X \ A }. Entonces tenemos una topología sobre Y, que no es la discreta, ni tampoco caótica.
Antes e continuar, debemos dar una definición para comparar las topologías sobre un conjunto. Es posible que sobre un mismo conjunto X tengamos dos topologías definidas τ y σ . Entonces, diremos que τ es más fina que σ , si todo abierto de σes un abierto de τ . Esto lo denotamos por σ ≤ τ .
En base a esta definición, podemos decir que la topología discreta es la más fina de todas las topologías y que toda topología es más fina que la topología caótica. Ellas representan los dos extremos entre los cuales se encuentran las otras topologías.
+ Problema para pensar: ¿ Podrías dar una topología sobre Y, más fina que τ ' , que contenga más abiertos y que no sea la topología discreta?
Solución: Por supuesto que sí es posible! J Es posible construir una topología más fina, formada por ocho elementos ( rogamos al lector efectuar la verificación).
Tomemos τ ' ' = { X, Æ, A, X \ A , C, X \ C, B ∪ D, A ∪C }
Para resumir, podemos hacer un recuento de todas las topologías que hemos encontrado en Y. Las topologías caóticas y discreta, serán denotadas por C y D. Tenemos entonces las relaciones:
C ≤ τ ' ≤ τ ' ' ≤ D.
3. Todo espacio métrico es un espacio topológico, con la topología dada por los conjuntos abiertos en el sentido de la métrica. Esta topología se llama topología inducida por la métrica. Recordemos que un conjunto A es abierto en un espacio métrico ( M ,d) , si todos los puntos son interiores.
4. Topologías equivalentes. dadas dos topologías σ y τ sobre un espacio X, diremos que ellas son equivalentes, o que definen la misma topología sobre X, si son iguales como conjuntos. Es decir, todo abierto en la topología ( X, σ ) es un abierto en la topología ( X,τ ).
En un espacio topológico un conjunto es cerrado si su complemento es abierto.
5. Métricas equivalentes. Dos métricas d1 y d2 sobre un conjunto M se dicen equivalentes si existen constantes positivas c y k, tales que
d1 ( x, y) ≤ c d2 (x ,y) ≤ k d1 ( x, y)
| Un espacio topológico X se dice que es del tipo T 1, si {a} es cerrado en X, para todo a en X. |
Ejemplo: Sea X = { a, b, c, d} con una topología τ , entonces ( X, τ ) es un espacio T 1 si τ es la topología discreta ¿ Será posible hallar una topología menos fina sobre X para que dicho espacio sea del tipo T 1?
|
Un espacio topológico X es del tipo T2 , o Hausdorff, si para cada par de puntos a y b en X, existen abiertos disjuntos U y V que los contienen y además U ∩V = Æ .
|
Todo espacio métrico es un espacio de Hausdorff.
| Sea ( X, τ ) un espacio topológico. Una base de abiertos para la topología , es una subfamilia ϐ, de τ, tal que para cada U abierto y a Î U, existe un abierto V en ϐ, que cumple: a Î V Í U. |
Ejemplo: En un espacio métrico, las bolas abiertas forman una base para la topología inducida por la métrica.