
|
¿Qué es la Topología? |
La topología es una ciencia que ha tenido orígenes diversos en la historia del pensamiento matemático. Es un tipo de geometría que estudia propiedades distintas a las métricas, como ángulo y distancia. La topología es una rama de la matemática que estudia las propiedades de los objetos invariantes bajo la acción de transformaciones continuas. Mas adelante serán definidas ésta cosas con todo el rigor matemático posible. Una transformación continua sobre un objeto es algo que lo deforma, lo sube, lo baja, lo voltea, lo mueve de un lado a otro, pero no lo rompe ni lo pega sobre si mismo. Por ejemplo si tenemos una banda de caucho y sobre esta banda dibujamos un círculo, entonces al estirar el caucho el circulo cambia deforma, pero hay cosas que no cambian: por ejemplo el interior del circulo original se conserva dentro del interior del circulo deformado. También en el circulo, el borde o la circunferencia es una línea continua sin interrupciones; lo mismo ocurre en el circulo deformado.




Podemos decir que C' es una imagen topológica de C o bien que las figuras C y C' son topológicamente equivalentes.
El Problema de los siete puentes de Königsberg.
Históricamente, el primer problema de topología planteado por matemático alguno fue el famoso Problema de Los Siete Puentes de Königsberg. En aquella ciudad existen dos islas sobre un río, las cuales se conectan a tierra mediante siete puentes. El problema consiste en hacer un recorrido que pase por todos los puentes y regresar al punto de partida, habiendo cruzado cada puente una sola vez ( ver la figura). Curiosamente, era un problema de matemáticas en el cual no se trataban cantidades, ni ángulos, ni medidas. Entonces se pensó que se trataba de algo sobre la geometría de la posición de los objetos. Un problema sobre el espacio. Algo totalmente nuevo en matemáticas, y que Leonhard Euler, resolvió y publicó en 1736 en un artículo titulado: Solutio problematis ad geometriam situs pertinentis.
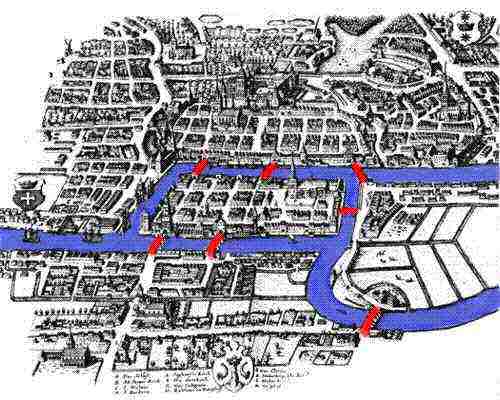
La técnica emplead por Euler, consistió en simplificar el problema, expresando las ideas en forma de un grafo, en donde solo aparecen vértices( nodos) y lados. Se demuestra que la trayectoria es imposible.
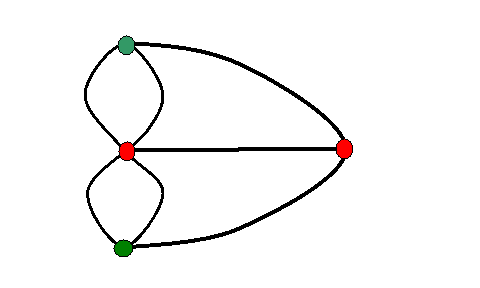
Los puntos rojos representan las dos islas, los puntos verdes representan la tierra en cada una de las orillas y los arcos en negro son las trayectorias posibles para ir de un lugar a otro. Podemos decir que un punto o nodo es de orden par si al mismo llegan un número par de arcos o trayectorias. Caso contrario diremos que el punto es de orden par. Euler descubrió que para poder hacer el recorrido completo es necesario y suficiente que haya exactamente dos puntos de orden par en el grafo.
La fórmula para los poliedros
En 1750, el mismo Euler, en una correspondencia con el matemático Goldbach, menciona una fórmula para los poliedros sobre el número de caras, vértices y aristas, que ningún geómetra de la antigüedad había sospechado. la fórmula de Euler viene dada por la sencilla relación
v - e + f = 2
donde v = número de vértices, e = número de lados y f = número de caras.
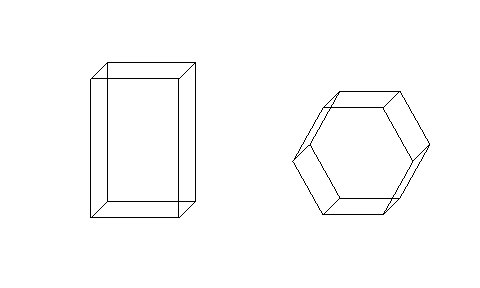
Nuevamente tenemos aquí una propiedad de los objetos que no depende de su tamaño, ni de la posición de los mismos en el espacio. la fórmula de Euler es un ejemplo de un invariante topólogico. Es decir, algo que no cambia, al hacer una pequeña deformación sobre el objeto. Euler dio una demostración incompleta de su fórmula en 1752. Más adelante, otro matemático muy poco conocido, Antoine-Jean Lhuillier continuó trabajando en la fórmula de Euler. Probó que es cierta para sólidos sin huecos. Si el sólido tiene g huecos, Lhuillier , probó que se tiene la fórmula
v - e + f = 2 - 2g
Superficies extrañas.
El estudio de algunas superficies tridimesionales algo extrañas, por parte de algunos geómetras también contribuyó al nacimiento de la Topología, a mediados del siglo XIX. Möbius descubrió su famosa banda que era una superficie de una sola cara. Möbius publicó una serie de propiedades de esta superficie en 1865. Sin embargo Johan Benedict Listing se adelantó a Möbius y estudió con mayor profundidad las propiedades de esta banda, como la conectividad y las componentes de superficie. Listing estudió las ideas topológicas propuestas por Gauss. Aunque Gauss nunca publicó ningún trabajo sobre topología, dio una prueba de tipo topológico sobre el teorema fundamental del álgebra, el cual estudiaremos en este curso. Fue este matemático alemán, Johan Benedict Listing, quien por vez primera utiliza la palabra Topología, en una monografía escrita en 1847.
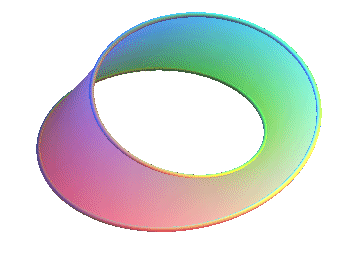
También mencionaremos la famosa superficie de Klein o botella de Klein, estudiada por Felix Klein en 1882. Este es un ejemplo de una superficie cerrada de una sola cara, sin ningún tipo de borde y que además no posee ni interior ni exterior. Otra superficie muy estudiada por los fundadores de la topología es el Toro ( en forma de rosca).
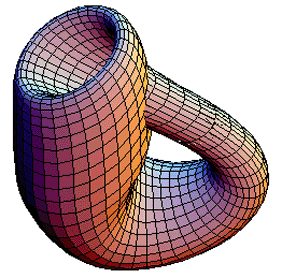

Entre los estudiosos de superficies con propiedades interesante, como la conectividad, también hay que señalar a Riemann quien desarrolló las superficies de Riemann en sus investigaciones sobre ecuaciones polinomiales con variable compleja en 1857.
Enlaces de interés.