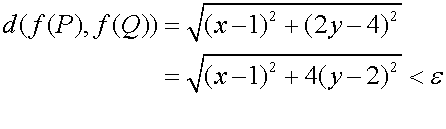Noción de continuidad
La continuidad es un concepto fundamental en el estudio de la topología. Muchos procesos naturales como el cambio en las condiciones meteorológicas en una región del espacio, se pueden modelar gracias a los sistemas dinámicos continuos. Podemos asociar a los cambios en un sistema, ciertas funciones matemáticas que dependen continuamente de algunos parámetros como el tiempo, la temperatura, la posición, la velocidad,..etc.

¿ Qué es la continuidad?

La continuidad es es pasarse uno la vida haciendo siempre lo mismo- dice Juan, uno de los estudiantes más aburridos del curso.

La continuidad es lo opuesto a la revolución - responde un revolucionario.

Todo lo contrario,- responde Margarita- podemos pasar de un estado a otro totalmente diferente mediante una transición continua.

Una curva continua es aquella cuerda que no se interrumpe- agrega otro de los estudiantes que se sienta al fondo del aula.

Todas las respuestas han sido correctas- dice el Profesor- pero alguien me puede responder  ¿ Que es la continuidad, sin hablar de la vida, una cuerda o la revolución? Nos sobran los ejemplos, pero necesitamos un solo concepto!

 

El concepto de continuidad se puede definir en los espacios métricos usando el concepto de distancia. El concepto de continuidad se define en primer lugar, localmente para cada punto. Luego se da una definición global de continuidad para todos los puntos de un cierto conjunto.

Sean (M, d) y (N, d')  dos espacios métricos y  f : N ——→ M es una función entre ellos. Diremos que f es continua en un punto a de N, si ocurre lo siguiente: cada vez que tomemos un punto x muy cercano a a, entonces la distancia entre las respectivas imágenes, f( x) y  f( a) se hace muy pequeña.

Si A es un subconjunto de M, entonces la función se dice continua en A, si es continua en todos los puntos de A.

Esta definición sin embargo es un poco vaga, pues no sabemos con precisión que quiere decir " muy cerca".

Por ejemplo, sea f : R2 ——→ R2 , la transformación del plano en sí mismo, dada por

f( x, y) = (2x , y)

Esta función,  llamada  dilatación horizontal del plano,  es un ejemplo de función continua en todo el plano.. Ella deforma los objetos del plano, manteniendo la altura de los mismos, pero doblando su anchura. Podemos imaginar la acción de la misma sobre sobre un circulo y un par de puntos situados a una distancia δ.

Esta transformación estira el plano horizontalmente, como si fuera una banda de caucho. Los dos puntos iniciales han sido separados un poco, pero todavía hay una proximidad entre ellos. Lo importante es que podemos hacer que las imágenes estén tan cercanas como se quieran, tomando las preimagenes muy cercanas.

Definiciones de Continuidad

 

1. Usando distancias

La función f es continua en un punto a, si para todo  ε > 0, existe un δ > 0, tal que

d( f( x), f( a)) < ε ,  si  d( x, a) < δ  .

 		  
2. Usando límites La función f es continua en un punto a, si
  1. f está definida en a.
  2. El límite de f( x) cuando x tiende hacia a existe y es iguala L.
  3. El valor de la función en el punto a es igual al límite anterior: f(a) = L.
  
3. Usando Bolas abiertas Sean (M, d) y (N, d')  dos espacios métricos y  f : N ——→ M es una función entre ellos. Diremos que f es continua en un punto a de N si para todo  ε > 0 , existe un  δ > 0, tal que

f (B ( a,  δ) )  Í  B( f (a), ε )

 

Muchos estudiantes me hacen la siguiente pregunta:

¿Cómo se calcula el delta, una vez conocido el epsilon ?

Veamos como se hace esto con un ejemplo concreto. Aquí se demuestra que la dilatación horizontal del plano es continua en el punto P ( 1, 2).

 

Usaremos la definición 1. Supondremos que alguien nos ha dado un número positivo ε > 0 y además nos ha hecho el siguiente requerimiento: ¿ A que distancia debe estar un punto Q( x, y) del punto P (1,2), para que la distancia entre las imágenes de ambos sea menos que ε ?

Partimos de este supuesto para poder responder a la pregunta. Tenemos entonces que

Por otra parte, sabemos que :

Para poder tener las dos desigualdades al mismo tiempo, debemos tener alguna manera de relacionar el épsilon con el delta. La clave viene dada por las dos expresiones radicales, que se pueden relacionar mediante la desigualdad:

Podemos ahora tomar a delta menor que epsilon medio y esto nos da la solución al problema.

 

Ejemplos de funciones continuas.

1) La función identidad 

I :  M ———→ M ,  x ——→ x , para todo x en M, es continua en todo punto a de M. En efecto, dado ε >0 , tómese δ = ε y entonces se tiene que d ( f( x) , f( a )) < ε , si d ( x, a) < δ.

2) Funciones Lipschitzianas.

Una función f  M ———→ N, se dice Lipschitziana, si existe una constante c, llamada constante de Lipschitz,  tal que

d( f (x), f( y) ) ≤ c. d ( x, y).

Toda función Lipschitziana es contínua en todas partes. En efecto, dado ε >0 , tómese δ = ε /c, y entonces se tiene que

d ( f( x) , f( a )) <   c. d ( x, y) < c.   ε /c = ε, si d ( x, a) < δ.

Ejemplo. La función  f  ℜ ———→ ℜ, dada por f( x) = | x | es Lipschitziana y por lo tanto continua. En efecto notemos que se tiene la desigualdad

 | f( x) - f( y) | =  | | x | -  | y | | ≤  | x - y |

Una función f  M ———→ N, se dice Localmente Lipschitziana, si para cada punto a de M, existe una bola abierta B (a, r) tal que la restricción de f a esta bola es lipschitziana. Es claro que toda función localmente lipschitziana es continua en cada punto.

Ejemplo. La función  f  ℜ ———→ ℜ, dada por f( x) =  x2  es localmente Lipschitziana y por lo tanto continua. En efecto notemos que en el intervalo ( a- r, a + r) se tiene la desigualdad

| f( x) - f( y) |  = | x2  -   y2  |   ≤ 2 | a + r | | x - y |

3) Isometrías

Una función f  M ———→ N se dice que es una isometría, si f es biyectiva y además

d( f (x), f( y) ) = d ( x, y).

para todos x e y en M. Por lo visto anteriormente, tendremos que toda isometría es continua.

Una isometría del plano es una transformación del plano en sí mismo que no cambia la forma de las figuras. Por ejemplo, las translaciones, rotaciones y reflexiones son ejemplos de isometrías.

4) Contracciones

Una función f  M ———→ N se dice que es una contracción si

d( f (x), f( y) ) < d ( x, y).            (*)

para todo par de puntos x e y en M.

5. Contracciones débiles

Una función f  M ———→ N se dice que es una contracción débil si

d( f (x), f( y) ) ≤ d ( x, y).            (*)

para todo par de puntos x e y en M.

 

Ejemplo 1: Si A es un conjunto cualquiera de un espacio métrico (M ,d), la función

f A : M ———→ ℜ  , f A( x) = d ( x, A) es una contracción débil . Esto se deduce de la relación  la relación

| d( a, A) - d ( b, A) | ≤ d ( a, b)

para todo par de puntos a y b en M..

Página principal                Siguiente Ü