|
Distancia entre subconjuntos |
Si A es un subconjunto de un espacio métrico M, y a es un punto cualquiera de M, entonces nos interesa hallar la distancia desde a hasta el conjunto A, lo cual se denota por d (a, A). Si a es un elemento de A mismo, entonces la distancia entre a y A, será cero. Si por el contrario, a está fuera de A, la distancia será el ínfimo de las distancias entre todos los puntos de A y a. Luego podemos definir
d( a, A) = inf { d( x, a), con x en A }
En el caso de los números reales, la distancia entre un número c y un conjunto A, la calculamos usando el valor absoluto
d( c, A) = Sup { | c - a | , tal que a Î A }
Por ejemplo, la distancia entre 1 y el intervalo I = (6 , 12) es igual a 5. ¿Por qué? Nótese, sin embargo, que ningún punto de I está a una distancia de 1 igual a 5.

En el dibujo de arriba tenemos otro elemento del espacio, representado por un punto rojo y el cual lo denotaremos por la letra b. Ciertamente, a y b están muy próximos. ¿Cuál será la diferencia entre d ( a, A) y d( b, A)? Esta diferencia, también debe permanecer pequeña , como lo comprobaremos a continuación:
Notemos en primer lugar, que si x es cualquier elemento del conjunto, se tendrá:
d (a, A) ≤ d ( a, x) ≤ d ( a, b ) + d (b, x )
Luego se debe tener d (a, A) - d ( a, b ) ≤ d (b, x ) , para todos los x en A. Pensemos que el lado izquierdo d e esta desigualdad es un valor constante y por lo tanto el ínfimo de todos los números d ( b, x), al hacer variar x en A, también satisface la desigualdad. Luego se tiene
d (a, A) ≤ d ( a, b ) + d (b, A )
Luego
d( a, A) - d ( b, A) ≤ d ( a, b)
Un argumento totalmente simétrico nos muestra
- d ( a ,b) ≤ d( a, A) - d ( b, A)
y de estas dos desigualdades se concluye
| d( a, A) - d ( b, A) | ≤ d ( a, b)
Si A y B son dos subconjuntos de un espacio métrico, M la distancia entre ellos viene dada por
d( A, B) = inf { d( x, y), con x en A e y en B}

Si A y B tienen intersección distinta del vacío entonces la distancia entre ellos será 0. El reciproco de esta afirmación no es cierto en general. Por ejemplo la distancia entre los números racionales y los irracionales, en la recta real con la métrica usual, es igual a cero. Sin embargo estos conjuntos no se interceptan.
Otro ejemplo, tomando como espacio métrico al plano R, con la métrica usual es el siguiente: Definimos A como el semiplano inferior al eje x y B al conjunto de puntos por encima de la gráfica de la función f( x) = 1/x ( ver el dibujo)
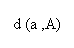
Entonces la distancia entre ambos conjuntos es igual a cero. Pero ellos no se interceptan.