En esta sección continuamos dando algunas definiciones básicas para el estudio de los espacios métricos. Son conceptos muy intuitivos, desde el punto de vista geométrico, y que pueden ser bien definidos usando la noción de conjunto abierto.

El Interior de A.

Para iniciar nuestra exposición, consideremos a R² ,  el plano euclideano con la métrica usual, y A  el conjunto formado por todos los puntos del primer cuadrante ( de color verde):

A =  {(x, y) en R² , tales que x > 0  e y > 0 }

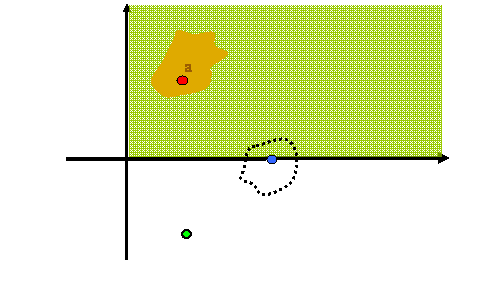
 Entonces el punto a = ( 3, 5) , de color rojo en el dibujo, es un punto interior de A. Hemos trazado una vecindad, de color marrón, que lo contiene y a su vez está contenida en A. Se puede mostrar que todos los puntos de A son puntos interiores.

Sea A un subconjunto de un espacio métrico M. Un punto a en A, se llama punto interior de A, si existe un abierto U conteniendo a a, tal que U Í  A.

Sea ahora el conjunto b, formado por el eje horizontal positivo

B =  {(x, y) en R² , tales que   x > 0 e y = 0 }

En el conjunto B, por otra parte, no hay puntos interiores. Un punto cualquiera de B, como el punto azul en la figura, no puede ser encerrado dentro de un conjunto abierto contenido en B. Hemos trazado un abierto, con la línea negra punteada, pero éste se sale de B.

El conjunto de todos los puntos interiores de un conjunto A, denotado por int (A) se llama el interior de A.

Se puede demostrar que A es abierto sí y sólo si todos sus puntos son interiores o también

A es abierto sí y sólo si A = int(A)

   La frontera de un conjunto A.

 En un conjunto A, vamos a considerar los puntos de la frontera. En M, pueden existir puntos b, tales que toda vecindad U que contiene a b contiene tanto puntos de A y como puntos del complemento de A. Estos son los llamados puntos frontera de A. El punto azul, en el dibujo de arriba es un punto frontera. El conjunto conjunto de todos estos puntos se llama la frontera de A, y se  denota por δ(A). En el ejemplo dado todos los puntos de B son parte de la frontera de A. ¿ Cuál es la frontera de A?

El exterior de A.

Un punto de M que se encuentra en el interior del complemento  A, se dice que es un punto exterior de A. Por ejemplo, el punto verde arriba está en el exterior de A. El exterior de A = int ( M \ A) estará formado por todos los puntos exteriores.

Tenemos la relación fundamental que liga estos tres conceptos como una unión disjunta..

 M = int (A)  ∪ δ(A) ∪ext (A).

! Advertencia

Todos éstos conceptos estudiados en esta sección son relativos y dependen de la métrica. Por ejemplo so consideramos al conjunto B de arriba como un subespacio métrico unducido por la métrica de R, entonces tendremos

int (B) = B , δ (B) = {(0,0)}, ext (B) = { x Î R tales que  x < 0}

Por otro lado, podemos considerar a B como un subconjunto del espacio métrico de R² . Luego

int(B) =Æ , δ (B) = B, 

ext (B) = {(x, y) en R² , tales que  y ¹ 0 }∪{(x, y) en R² , tales que   x ≤ 0 e y = 0 }

Página Principal                 Siguiente