|
Noción de límite |
Consideremos la sucesión de números 0, 1/2, 4/5, 1, 8/7, 5/4, 4/3, 7/10, 20/13,......:podemos representar los valores sobre una recta numérica
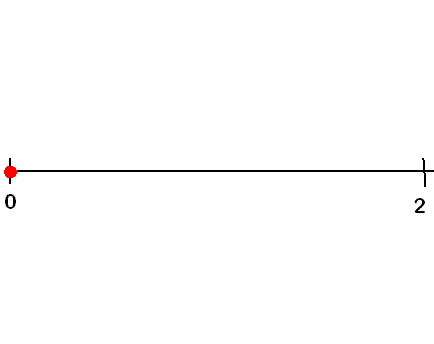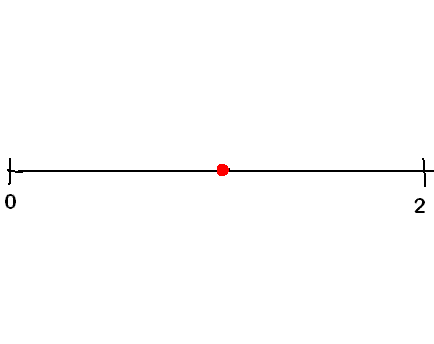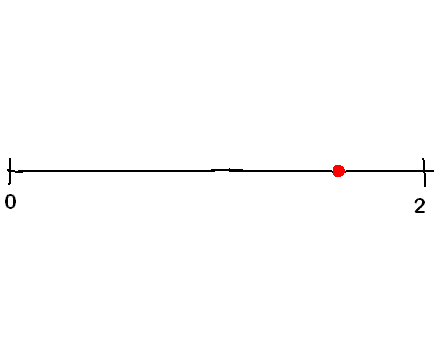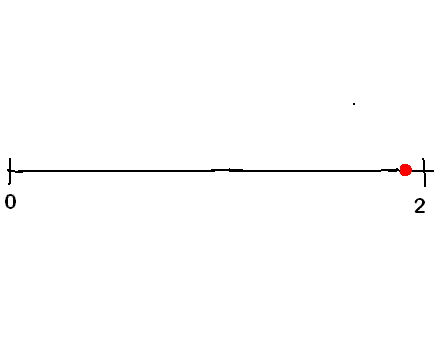
Vemos como los valores se aproximan a 2 en forma progresiva.
Podemos dar una notación especial para esta sucesión ( un poco de simbolismo siempre es necesario para poder expresar las ideas con claridad). Hacemos entonces
| a0 = 0 | a5 = 5 / 4 |
| a1 = 1 /2 | a6 = 4/3 |
| a2 = 4/ 5 | a7 = 7 / 5 |
| a3 = 1 | a8 = 16 / 11 |
| a4 = 8 / 7 | a n = 2n / n + 3 |
Podemos afirmar, en base a un conocimiento experimental, que la distancia entre los términos de la sucesión y 2, o lo que es lo mismo, | a n - 2 | se hace muy pequeño, a medida que n crece. Se dice que entonces que el límite de la sucesión {a n} es igual a 2. Nótese que en este caso, ningún valor de la sucesión es igual a 2! Lo importante aquí es que podemos hallar términos de la sucesión tan cercanos a 2 como se desee.
| Por ejemplo , si Juan le pide a María -Quiero un término de la sucesión que esté a menos de una milésima de 2. Entonces María le responde -Si tomo n = 10000, entonces a 10000 = 1,9994001799460161951414575627312.
|
Juan y María pueden pasar días enteros en este juego y siempre ganará María. ¿ Por qué?
Si ( M, d) es un espacio métrico y { a n } es una sucesión en M, entonces diremos que el límite de la sucesión cuando n tiende a infinito es L, o que la sucesión converge a L , si para todo ε >0, existe un número natural grande N0 , tal que
d( a n , L ) < ε , para todo n ≥ N0.
En otras palabras, dado un ε > 0 , podemos tener todos los puntos de la sucesión { a n } , a partir de n0, dentro de la bola abierta B ( L, ε).
Una sucesión { a n } en un espacio métrico M, es una función f : N ——→ M , donde la imagen de un número natural n, la representamos por f( n) = a n . Para denotar esto, usamos el simbolismo
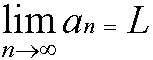
El límite de una función
Si ahora tenemos dos espacios métricos ( M, d ) y (N, d') y f es una función f : M ——→ N , examinaremos el concepto del límite de una función en un punto. Primero daremos una definición en términos de distancias.
|
Sea a perteneciente a N entonces el límite de f (x), cuando x tiende a a es L , y lo denotamos por
si para todo ε > 0 , existe un δ > 0, tal que d´( f( x) , L) < ε , si d ( x, a ) < δ .
|
Daremos una segunda definición de límite, equivalente a la anterior, en términos de bolas abiertas.
|
Sea a perteneciente a N entonces el límite de f (x), cuando x tiende a a es L , y lo denotamos por
si para todo ε > 0 , existe un δ > 0, tal que f (B ( a, δ) ) Í B( L, ε )
|
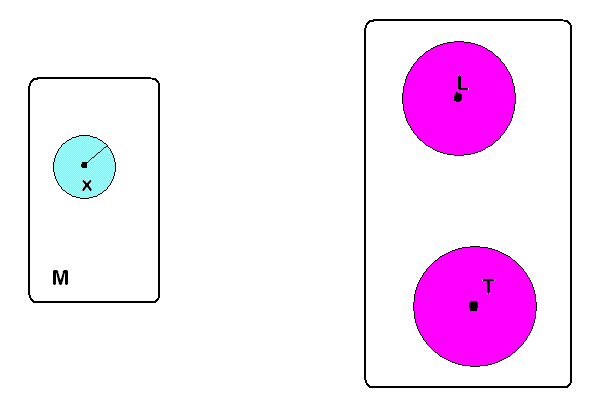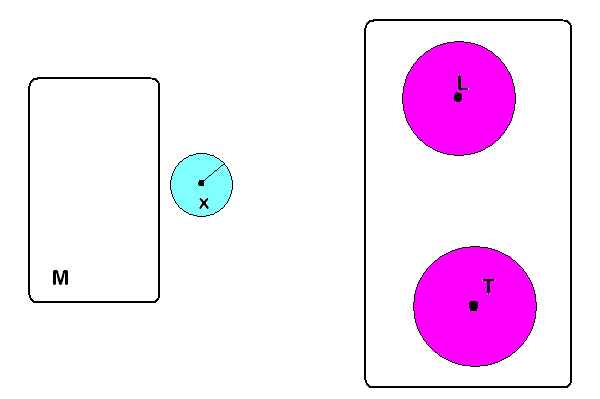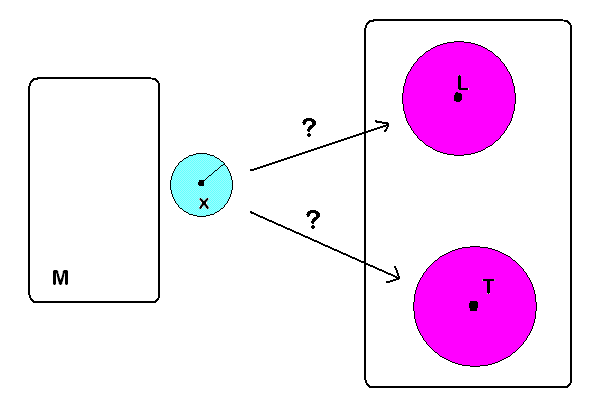
Podemos imaginar la acción de una función sobre la bola abierta con centro en x, de color celeste: la función lleva la bola dentro de la bola con centro en L ( de color magenta)
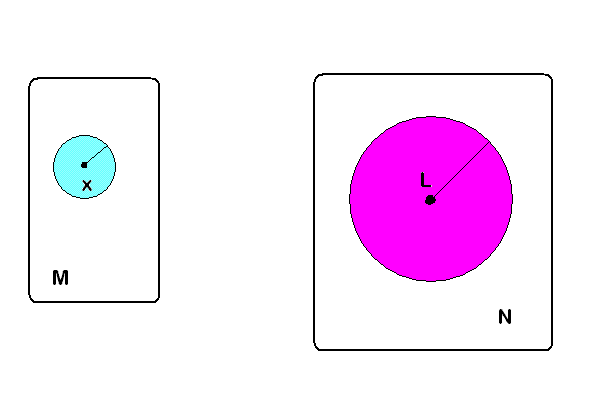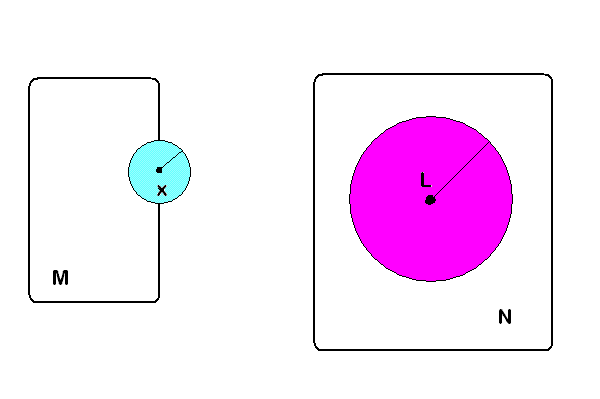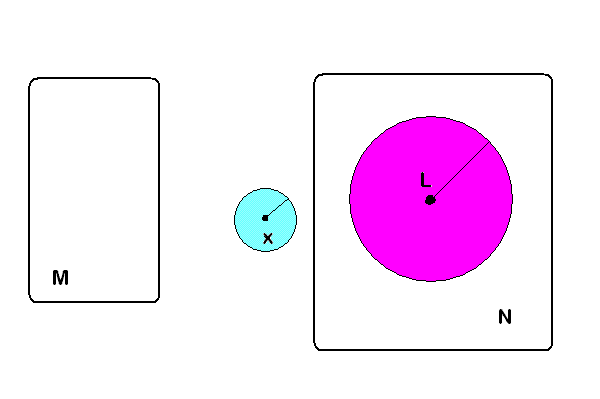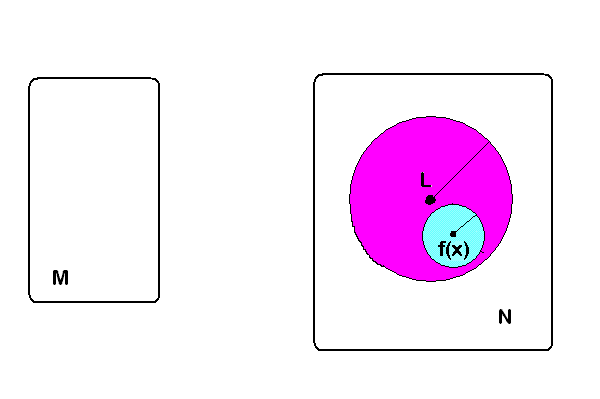
Observación: Si a es un elemento de un espacio métrico M y f es una función de M en otro espacio métrico N, y el límite de f( x) cuando x tiende a a es L, entonces el valor de L es único. NO puede ser posible que f( x) tienda hacia otro valor T, distinto de L.
ËËËËËËË
Para probar este hecho, podemos tomar dos bolas abiertas en el espacio N, una centrada en L y la otra en T, de tal manera que no se corten. Entonces ( aplicando la definición de límite en ambos casos ) podemos hallar una bola centrada en a B (a, δ ) de color celeste, la cual va a ser enviada por la función en dos lugares distintos simultáneamente. Esto por supuesto es una contradicción. Ejercicio: dar una demostración formal.