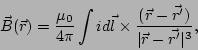Next: Flujo Magnético
Up: Electrodinámica
Previous: Campo Magnético
Si el origen del campo magnético son las cargas en movimiento o corrientes eléctricas,
entonces podemos considerar las fuerzas magnéticas que se ejercen elementos
de corriente 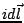 entre si. Sean los lazos de corriente
entre si. Sean los lazos de corriente 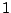 y
y 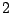 . La fuerza diferencial
que ejerce el lazo
. La fuerza diferencial
que ejerce el lazo 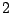 sobre un elemento diferencial de corriente del lazo
sobre un elemento diferencial de corriente del lazo 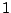 es
es
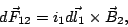 |
(29) |
donde 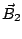 viene dado por la Ley de Biot-Savart
viene dado por la Ley de Biot-Savart
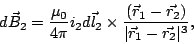 |
(30) |
donde
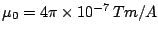 es la Permeabilidad del vacío y se determina experimentalmente.
En general, una corriente
es la Permeabilidad del vacío y se determina experimentalmente.
En general, una corriente 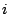 produce un campo magnético
produce un campo magnético
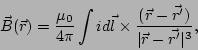 |
(31) |
donde 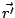 es el vector posición del elemento diferencial de corriente
es el vector posición del elemento diferencial de corriente 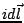 .
.
Willians Barreto
2006-10-06
![]() entre si. Sean los lazos de corriente
entre si. Sean los lazos de corriente ![]() y
y ![]() . La fuerza diferencial
que ejerce el lazo
. La fuerza diferencial
que ejerce el lazo ![]() sobre un elemento diferencial de corriente del lazo
sobre un elemento diferencial de corriente del lazo ![]() es
es