


Next: Cálculo estadístico de la
Up: Termodinámica
Previous: Cálculo cinético de la
Si hacemos un experimento y medimos la distribución de velocidades en un gas monoatómico a baja densidad,
observaremos que el histograma se ajusta muy bien a la siguiente función propuesta por Maxwell
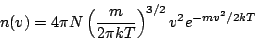 |
(16) |
donde 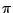 es el famoso
es el famoso 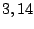 . Esta es la función de distribución de velocidades.
. Esta es la función de distribución de velocidades.
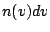 representa el número de moléculas con velocidades entre
representa el número de moléculas con velocidades entre 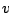 y
y 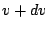 . Así,
. Así,
debe ser N, y en efecto lo es.
Hagamos otra pruebita a la función de distribución de Maxwell. Calculemos el promedio de la velocidad cuadrática.
Se encuentra que este promedio es (ver problema 11 del primer problemario):
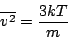 |
(17) |
y en consecuencia la 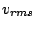 coincide con el cálculo cinético, como debe ser
coincide con el cálculo cinético, como debe ser
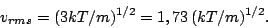 |
(18) |
Ya que podemos confiar en la función de distribución de Maxwell, calculemos ahora la velocidad promedio, resultando
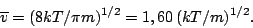 |
(19) |
La velocidad más probable corresponde al máximo de la función de distribución
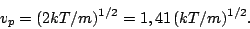 |
(20) |
Observe que
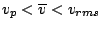 .
.
La distribución de velocidades explica por qué el agua se evapora sin alcanzar la temperatura de ebullición y
por qué la evaporación es un proceso de enfriamiento.
Explica por qué las reacciones químicas aumentan cuando aumentamos la temperatura. También por qué el hidrógeno
se escapa con mayor facilidad que el oxigeno y el nitrógeno de nuestra atmósfera.



Next: Cálculo estadístico de la
Up: Termodinámica
Previous: Cálculo cinético de la
Willians Barreto
2006-04-24