


Next: Formulación de Clausius para
Up: Termodinámica
Previous: Procesos reversibles e irrevesibles
Una máquina de calor es un dispositivo que convierte calor en trabajo útil. Esto es, la energía fluye
hacia el sistema en forma de calor y parte de esta energía sale del sistema en forma de trabajo
hecho sobre el entorno. Ustedes conocen el proceso inverso, trabajo convertido en calor: las fuerzas
de fricción convierten el trabajo en energía interna y esta energía puede ser transferida al entorno en
forma de calor. Otro ejemplo es el trabajo mecánico sobre un generador eléctrico que envía corriente a sus
hogares, donde un calentador eléctrico convierte el trabajo en energía interna, la cual fluye como
calor. Un cilindro con pistón (tapa móvil) que contiene un gas ideal y sobre un reservorio térmico a cierta temperatura es un
ejemplo representativo de una máquina de calor. Permitimos que el gas se expanda a isotérmicamente.
El calor entra al gas desde el reservorio y el gas realiza trabajo. Listo, inventamos la máquina de calor, salvo
algunos ``detalles'' tecnológicos. Como la temperatura en constante la energía interna no cambia,
obteniéndo así un dispositivo que convierte calor en trabajo. Pero nuestra máquina de calor
queriere algunos ajustes para que resulte útil. Por ejemplo, no puede operar indefinidamente. El cilindro
tiene una altura definida. Una maquinita más útil es la que opera en un ciclo, regresando al
punto de partida despues de realizar cierto trabajo y así indefinidamente.
Supongamos que el ciclo se realiza reversiblemente. Un ciclo en el sentido horario realiza trabajo negativo,
es decir, el trabajo realizado por el sistema, que es justo lo que se busca. Un posible ciclo para una máquina
de calor puede ser:
- Aumentamos la temperatura manteniendo el volumen constante (proceso isócoro), la presión aumenta;
- Aumentamos la tempetatura manteniendo la presión constante y permitiendo que el gas se expanda (aumento de volumen
en un proceso isóbaro);
- Disminuioms la temperatura mantiendo el volumen constante (proceso isócoro), la presión disminuye;
- Disminuimos la temperatura manteniendo la presión constante mientras el volumen decrece a su valor inicial
(compresión isóbara).
En los procesos 1 y 2 el calor es positivo, es decir, entra; en los procesos 3 y 4 el calor sale. El calor entrante es
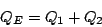 |
(32) |
y el calor saliente
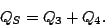 |
(33) |
Así, el calor neto es
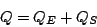 |
(34) |
o equivalentemente
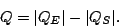 |
(35) |
En el ciclo 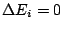 , por tanto segón la primera Ley de la Temodinámica,
, por tanto segón la primera Ley de la Temodinámica, 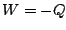 por lo que
podemos escribir
por lo que
podemos escribir
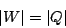 |
(36) |
y en consecuencia
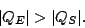 |
(37) |
Muy bien, ahora definamos el rendimiento o eficiencia de la máquina de calor como la razón entre la cantidad neta de trabajo
realizado por el gas sobre el entorno durante un ciclo y la cantidad de calor entrante:
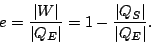 |
(38) |
Si lográramos que 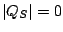 la máquina fuera perfecta, pero la segunda Ley de la Termodinámica nos dice
que esto es imposible, es decir, no es posible construir una máquina de calor
la máquina fuera perfecta, pero la segunda Ley de la Termodinámica nos dice
que esto es imposible, es decir, no es posible construir una máquina de calor 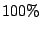 eficiente (
eficiente (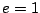 ).
La segunda Ley de la Termodinámica en la formulación de Kelvin-Planck nos dice:
).
La segunda Ley de la Termodinámica en la formulación de Kelvin-Planck nos dice:
No es posible en un proceso cíclico convertir calor completamente en trabajo sin que ocurra otro cambio.
En otras palabras, es imposible reducir 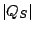 a cero. Pero ¿Por qué no?.
a cero. Pero ¿Por qué no?.
Observe el énfasis que se hace en la palabra cíclico. Hemos
visto que el calor inyectado a un gas ideal se puede transformar
completamente en trabajo, pero después de la expansión el
gas no se encuentra en el mismo estado inicial. Para que el gas
regrese al mismo estado inicial, tiene que ceder calor.



Next: Formulación de Clausius para
Up: Termodinámica
Previous: Procesos reversibles e irrevesibles
Willians Barreto
2006-04-24
![]() a cero. Pero ¿Por qué no?.
a cero. Pero ¿Por qué no?.