


Next: Entropía
Up: Termodinámica
Previous: Formulación de Clausius para
Se puede demostrar que la formulació de Kelvin-Pack y la de Clausius son equivalentes. Pero no nos avocaremos
a esto. Más bien nos preguntamos lo siguiente: ¿Cual es la máquina térmica ideal? Además,
respondiendo esta pregunta nos acercaremos a la variable de estado denominada Entropía que nos conducirá
a una formulación fundamental de la segunda Ley de la Termodinámica.
El ciclo ideal es el de Carnot, que procesa a un gas ideal como sustancia de trabajo y opera entre dos
isotermas y dos adiabáticas. Así el trabajo realizado en el ciclo es el óptimo con el uso eficiente
del calor entrante. Se puede demostrar fácilmente que el rendimiento es
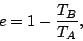 |
(41) |
donde 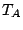 t
t 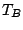 son las temperaturas de trabajo alta y baja, respectivamente. O invirtiendo el ciclo que la
eficacia es
son las temperaturas de trabajo alta y baja, respectivamente. O invirtiendo el ciclo que la
eficacia es
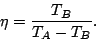 |
(42) |
Podemos decir entonces que el rendimiento o la eficacia en un ciclo de Carnot dependen sólo de las temperaturas
de los dos reservorios térmicos entre los cuales opera la máquina térmica.
Hemos usado un gas ideal como sustancia de trabajo; se pueden usar otras
sustancias. Las máquinas de calor reales no operan en ciclos reversibles.
La máquina de Carnot nos aporta información útil sobre el comportamiento
de cualquier máquina térmica. Nos indica cuál es el límite superior
en el rendimiento o eficacia de una máquina real y hacia dónde debemos
apuntar nuestros esfuerzos.
Teorema de Carnot:
El rendimiento o eficacia de cualquier máquina térmica que opera
entre dos temperaturas especiíficas nunca puede exceder el rendimiento
o eficacia de una máquina de carnot que opere entre las dos mismas
temperaturas.



Next: Entropía
Up: Termodinámica
Previous: Formulación de Clausius para
Willians Barreto
2006-04-24