|
Preguntas y Respuestas Marta Sananes Instituto de Estadística Aplicada y Computación IEAC Facultad de Ciencias Económicas y Sociales. Universidad de Los Andes Revisado Septiembre 1998. |
Contenido:
- ¿ Qué
es un computador ?
¿ Qué clase de procesamiento puede hacer el computador ?
¿ Dónde debe estar ubicada la información que se va a procesar ?
¿ Cómo procesa el computador la información alojada en su memoria ?
¿ Qué parte del computador reconoce y ejecuta las instrucciones ?
¿ Cuántas instrucciones puede ejecutar el CPU a la vez ?
¿ Dónde tiene que estar el programa ?
¿ Cómo hace un CPU para ejecutar todas las instrucciones de un programa ?
¿ Cómo sabe la ALU sobre cuál información debe operar la instrucción en ejecución ?
¿ Cómo se transfieren las instrucciones y los datos entre el CPU la memoria ?
¿ Cómo se introducen los datos y los programas a la memoria del computador ?
¿ Cómo se almacena la información que se introduce al computador ?
¿ Cómo se representa la información en la memoria ?
¿ Cómo es que podemos introducir números, textos, información lógica y cómo hace el computador para retenerlos ?
¿ Qué son HARDWARE Y SOFTWARE ?
¿ Qué es un Sistema Operativo ?
¿ Qué son y por qué hay tantos Lenguajes de Programación ?
Apéndice A: Sistemas de Codificación
de Caracteres
Apéndice B: Sistema de Numeración
Binario
¿ Qué es un computador ?
- Un computador es una máquina para
procesar
información. Un computador digital puede procesar(manipular,
transformar, operar) información
que esté codificada:
representada mediante símbolos.
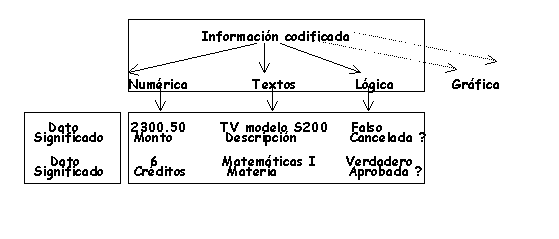
Cada unidad de información es un dato. Los datos o información
codificada pueden ser de diversos tipos:
¿ Dónde debe estar ubicada la información que se va a procesar ?
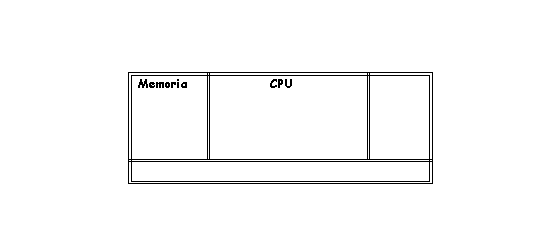
- La información o datos a procesar
tienen que estar colocados en la MEMORIA o Almacenamiento Principal,
uno de los componentes de un sistema
computador.
Esquemáticamente:
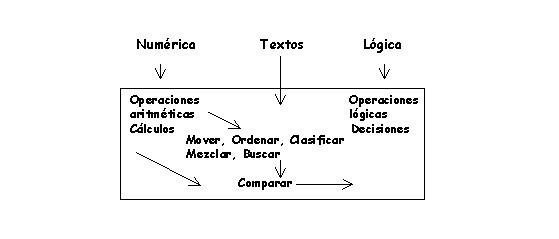
- Ejecutando las instrucciones contenidas en
un PROGRAMA. Todo computador es capaz de efectuar operaciones
elementales de un repertorio básico de operaciones o instrucciones
con el cual fué diseñado por sus fabricantes (Instrucción
Set).
Un programa ejecutable es una secuencia de instrucciones del repertorio básico.
- La capacidad de procesamiento de un computador
reside en uno de sus componentes, el componente principal: la Unidad Central
de Procesamiento (UCP o CPU: CentralProcesor Unit) o simplemente
Procesador
- En principio una sola. Pero en CPUs de alto
rendimiento hay capacidad de solapamiento entre instrucciones sucesivas.
Los computadores paralelos poseen varios CPUs de alto rendimiento trabajando
simultáneamente. Aún computadores sencillos usualmente, además
del CPU que ejecuta los programas, tienen varios procesadores dedicados
a distintas tareas, como el control de un dispositivo periférico,
por ejemplo.
- También en la memoria, como cualquier
otra información codificada.
- Internamente un CPU tiene varios componentes.
Uno de ellos es la Unidad de Control (UC) que tiene un registro
de instrucción (IR) -un registro es una pequeña memoria interna-
en donde se almacena una copia temporal de la instrucción
que esté en ejecución y otro registro en donde
lleva la dirección u ubicación en la Memoriade la
siguiente instrucción a ejecutar.
- Registros de datos: registros para alojar temporalmente valores de los operandos mientras se ejecuta una instrucción, resultados de operaciones, direcciones de operandos en memoria.
- Manejo de interrupciones: necesario en computadores con capacidad multitarea, es decir computadores que puedan alternar la ejecución de varios programas, metafóricamene como un maestro de ajedrez jugando una partida simultánea con varios jugadores.
Otro componente del CPU, la Unidad Aritmético-Lógica (UAL), se encarga de ejecutar propiamente la instrucción cargada en el registro IR. Cuando la UAL termina de ejecutar una instrucción, la UC carga (load) desde la memoria la instrucción alojada en la dirección indicada por el registro de dirección y éstapasa a ser inmediatamente la intrucción en ejecución, y así sucesivamente hasta que se llegue a una instrucción que indique el final del programa.
Para iniciar la ejecución de un programa, es necesario colocar en el registro de dirección la dirección de memoria de su primera instrucción.
Todo computador viene provisto también de un procedimiento inicial de arranque que se activa automáticamente al encender el equipo. Este proceso automático de arranque se encarga de colocar la dirección de la primera instrucción de un programa precargado -programa inicial de arranque- y de allí en adelante la ejecución de programas es como una especie de carrera de relevo.
Típicamente el procedimiento inicial coloca la dirección de la primera instrucción del programa inicial de arranque en el IR del CPU. Este programa inicial luego de chequear el estado normal de los componentes termina comunicándose con algún dispositivo periférico predeterminado desde el cual se carga usualmente un componente básico inicial de un Sistema Operativo el cual continuará controlando la actividad del computador según las órdenes de los usuarios hasta que el computador se apague normalmente o por alguna falla.
Proceso General del Computador
Otros elementos dentro de un CPU son:
El siguiente gráfico muestra esquemáticamente
los componentes de un computador:
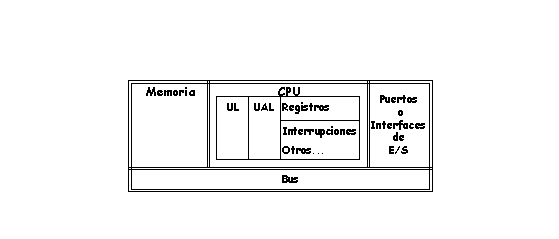
- Una instrucción típica de un
computador contiene dos partes: una parte es el códigode
operación que identifica el tipo de operación
a realizar y la otra parte contiene la o las referencias
a los operandos. Una referencia a un operando puede ser directamente
el valor del operando o la dirección del lugar donde se encuentra
el valor, que puede ser un lugar en la memoria o uno de los registros del
CPU.
Por ejemplo, una instrucción del repertorio de un procesador puede indicar en su parte de código de operación que se haga una SUMA y en la parte de los operandos, que se sumen los valores que están guardados uno en el registro A del CPU y el otro en la posición 1000 de la memoria, dejando el resultado en el mismo registro A.
¿ Cómo se
transfieren las instrucciones y los datos entre el
CPU la memoria ?
- Se transfieren através de canal de
comunicación llamados BUS, otro tipo de componente delcomputador.
Por medio del Bus se realizan generalmente las comunicaciones entre todos
los componentes de un computador.
- Existen dispositivos externos al computador
que se conectan a él a través de otro tipo de componentes:
Puertos o Interfaces de Entrada/Salida (I/O por Input/Output). Por los
Puertos se conectan dispositivos y Controladoras de dispositivos que poseen
su propia capacidad de procesamiento, como los contraladores de discos.
También se los ha llamado Canales.
Los dispositivos externos o periféricos pueden diferenciarse en dos clases: medios de comunicación y medios de almacenamiento secundario.
Los medios de comunicación son dispositivos para la comunicación del computador con los usuarios. Se diseñan para que en un lado de la comunicación acepten acciones de usuarios o les presenten información significativa -textos, gráficos, sonidos- mientras que del otro lado las acciones o la información se corresponden con representaciones internas. A esta clase corresponden teclados, pantallas, ratones, digitalizadores, lectores ópticos, micrófonos, cornetas.
- Los medios de almacenamiento o almacenamiento
secundario son dispositivos capaces de almacenar y recuperar hasta
grandes cantidades de información en volúmenes de almacenamiento
de tipos electromagnéticos como son discos duros o flexibles, cintas.
- Permiten acceso rápido a información que se usa reiteradamente, evitando tener que repetir manualmente su ingreso que además de lento es susceptible a errores.
- Permiten el acceso controlado del computador a cantidades grandes de información -incluyendo programas- que por su tamaño no caben en su memoria principal.
- Sirven como medios de almacenamiento masivo.
- Sirven como medios de comunicación entre computadores. Usuarios de computadores en red pueden tener acceso a información almacenada en computadores remotos. Los medios que soportan volúmenes desmontables se pueden trasladar de un computador a otro y montarse a voluntad según requimientos de la operación de los programas. Esta característica además permite la comunicación dentro de un mismo computador de información entre distintas sesiones de ejecución de programas.
Son necesarios porque:
El almacenamiento en medios secundarios
permite el desarrollo de Sistemas de Información, al facilitar la
planificación de tareas ya sean concurrentemente compartiendo la
misma información o por etapas sucesivas en forma de cadenas de
procesamiento donde la salida de una etapa puede ser la entrada para una
o más etapas subsiguientes.
Por varios años se usaron a la vez como medio de comunicación y de almacenamiento las cintas y tarjetas perforadas de papel, que cayeron en desuso cuando se desarrollaron y se hicieron económicamente accesibles los medios actuales más eficientes.
- Así complementamos el esquema del
Computador com sistema:
S I S T E M
A C O M P U
T A D O R
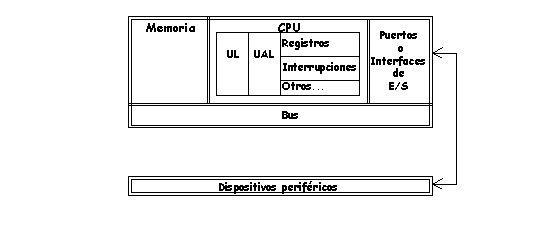
- La Memoria es un almacén de información
al cual el CPU tiene acceso directo tanto para poner datos como
para recuperarlos. Está organizada en forma de una secuencia
de unidades de almacenamiento elementales direccionables.
Podemos representarla como un gran pizarrón cuadriculado donde las casillas están numeradas desde 0 a m, para un total de (m+1) casillas usables.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ |
| ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ | ........ |
| m |
Al igual que en el pizarrón, cualquier casilla puede estar vacía o tener algo escrito y lo escrito permanecerá allí hasta que se lo borre y se reescriba otra cosa. Pero, las memorias ordinarias de computadores son volátiles: sólo mantienen la información mientras el equipo permanezca encendido.
Cada casilla es accesible independientemente tanto para escribir (guardar) como para leer (recuperar) un dato una vez especificada su dirección. A este tipo ordinario de memoria se le llama RAM por Random Access Memory.
Los computadores también vienen equipados
con memorias tipo ROM por Read Only Memory, que son memorias de
tipo permanente que sólo pueden ser leídas, no escritas.
Los fabricantes las usan para suministrar
con el equipo el programa inicial de arranque, que se ejecuta automáticamente
al encender el equipo, así como otros elementos.
A diferencia también del pizarrón,
lo escrito en cada casilla o byte tiene una estructura fija.Típicamante,
en una memoria de computador, un byte tiene 8 elementos llamados
cada uno bit, y cada bit puede contener la
representación
de un valor 0 o de un valor 1.
- Información lógica: Este tipo de información sólo tiene dos valores posibles: Verdadero (True) o Falso (False). Para almacenar un valor lógico basta con un bit, conviniendo arbitrariamente que el valor 1 equivale al Verdadero y el 0 al Falso. A nivel de instrucciones de la máquina, es posible direccionar un bit particular dentro de un byte.
- Texto: Para poder almacenar textos, es decir, información en forma de secuencias de caracteres alfanuméricos como letras del alfabeto, dígitos, signos de puntuación, etc., se establece una codificación que le asigna a cada símbolo representado una configuración particular de bits.
Usando solamente un byte para representar cada caracter alfanumérico, y dado que un byte consta de 8bits,entonces se pueden formar 28 configuracionesdistintas desde 00000000 hasta 11111111. Es posible entonces codificar un alfabeto de hasta 28= 256 caracteres distintos, por ejemplo nuestro alfabeto con las letras mayúsculas y minúsculas, los 10 dígitos de signos de puntuación(,;..), operadores aritméticos (+-*/), etc.
- Información numérica: Las primeras aplicaciones de los computadores y una buena parte de las actuales son aplicaciones de cálculo, es decir, queremos utilizar el computador para efectuar secuencias de operaciones numéricas. Entonces tiene que ser posible almacenar información numérica con la cual el computador, o mas específicamente, el CPU pueda efectuar las operaciones aritméticas elementales con las cuales se construye cualquier proceso de cálculo.
00000000 = 0
00000001 = 1
00000010 = 2
00000011 = 3
00000100 = 4
................
11111111 = 255
- A la izquierda del signo = tenemos
las representaciones en el sistema de numeración
Binario de los números de la derecha que están
escritos en el sistema normal de numeración que todos
utilizamos, el sistema de numeración decimal.
La consistencia de este tipo de representación numérica se completa definiendo la operación de suma según la tabla:
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Ejemplo: El siguiente del número binario 00001010 (10 en decimal) se obtiene sumando 1:
00001010 +
1
________
00001011
(11 en decimal)
y el siguiente
00001011 +
1
________
00001100
(12 en decimal)
Detalles de este tipo de representación en el Apéndice B: Sistema de numeración Binario.
La representación anterior usando 8 bits nos permitiría tan solo efectuar algunas operacionesaritméticas con los números naturales del 0 al 255 lo cual es muy limitado. Mediante programación se superan las limitaciones del hardware, implementando algoritmos que realicen por ejemplo las operaciones aritméticas con representaciones más amplias en microcomputadores que tienen ese microprocesador como su CPU, valiéndose de la representación y operaciones básicas. Los procedimientos o rutinas que implementan la aritmética extendida pueden estar incluidos en los Sistemas Operativos o en los lenguajes de programación.
Un algoritmo es una especificación detallada de los pasos a seguir para resolver un problema.
Un computador más complejo, como un PC con procesador Pentium, puede operar con los siguientes tipos numéricos:
- Enteros cortos: Ocupan 2 bytes consecutivos o sea, 16 bits en total. Para poder representar signo de los números, se utiliza el primer bit del primer byte como bit de signo: 0 positivo, 1: negativo, en una representación en formato complemento a 1. Quedan entonces 15 bits para representar la magnitud del número, lo cual nos permite representar números naturales en el rango
- Fracciones y números reales: Con el uso de las calculadoras electrónicas nos hemos familiarizado con la llamada notación científica para representar números racionales y en general aproximaciones racionales de números reales, por medio de una mantisa y un exponente. Por ejemplo, el número 0.0000005 lo podemos escribir en unacalculadora como
- Representación de punto Flotante en Simple Precisión: En muchos procesadores, ocupa 4 bytes, o sea, 32 bits. El primer bit del primer byte se usa para representar el signodel número y el resto del primer byte, o sea, 7 bits para el exponente de base 16. Los 3 bytes restantes, o sea, 24 bits, se usan para representar la mantisa. El rango depende del diseño particular. Puede ser por ejemplo,
- Representación de Punto Flotante en Doble Precisión: Ocupa 8 bytes consecutivos. El uso del primer byte es igual que en la representación de Precisión Simple. Los 7 bytes restantes se usan para representarla mantisa. El rango de los números representables es el mismo también pero usualmente se logran entre 15 y 17 dígitos decimales de precisión.
- [0 .. (215
- 1) ] = [0..32767 ]
(Por qué? ¿ Cuántos números hay en ese rango ? )
El rango incluyendo positivos y negativos es
[- 215 .. (215 - 1 )] = [-32768..32767 ]
La capacidad de operar con este tipo derepresentación
de números esta en el CPU delequipo. El procesador Pentium y otros
procesadores también puede operar con
representaciones numéricas de enteroslargos,ocupando
4 bytes consecutivos permitiendoasí un rango de [-231..(231
- 1)]
- Una representación numérica
en cualquier sistema de numeración en forma de mantisa
y exponente con la restricción de que la mantisa
deba ser un valor comprendido dentro de un rango fijo, por
ejemplo, entre 0 y 1, se dice que es una representación
de punto flotante porque la posición
verdadera del punto queda determinada por el valor del exponente.La
utilidad de una representación de este tipo es que permite
conservar el máximo de dígitos significativos
para un tamaño fijo de representación.
Para operar eficientemente con este tipo derepresentación flotante, el computador debe tenerun procesador que incluya en su repertorio de instrucciones las operaciones elementales de aritmética con representación flotante ya sea en su CPU principal o como procesador adicional especializado para ello, llamado coprocesador matemático. Si no lo tiene, también se recurre a la programación de algoritmos para que un computador puede efectuar también la aritmética de punto flotante, aunque en forma menos eficiente en cuanto al tiempo de ejecución de las operaciones.
Modos de representación usuales en varios computadores son:
- en valores absolutos, con aproximadamente
6 a 7 dígitos decimales de precisión.
El formato y tamaño de estas representaciones
son parte de las características de diseño de los procesadores.
- Si toda la información dentro del
computador está representada en binario y el CPU sólo puede
efectuar operaciones elementales, ¿cómo es entonces que hay
programas con instrucciones complejas escritas con el alfabeto ordinario,
cómo es que los datos numéricos los presentemos al computador
en el sistema decimal ordinario y que así mismo recibimos sus resultados
?
- Sistemas Operativos
- Ensambladores, Compiladores o Interpretadores de lenguajes de Programación.
- Sistemas o Paquetes para aplicaciones específicas.
La explicación está en que aprovechemos trabajo de programación acumulado.
Así como, por ejemplo, cuando alguien quiere hacerse un traje aprovecha materiales elaborados como telas, tijeras, agujas, hilos, cinta métrica, alfileres, etc., productos de los conocimientos y experiencias acumuladas por la humanidad y del trabajo de quienes participaron en su fabricación, así también cada vez que nos sentamos a trabajar con el computador estamos aprovechando, casi sin notarlo, la experiencia, conocimientos y el trabajo de otros diseñadores y programadores.
Estos productos elaborados en nuestro caso
son programas o conjuntos de programas de los siguientes tipos:
Bajo el término Hardware
designamos todo el conjunto de componentes físicos, funciones y
características propias del equipo en sí y bajo el término
Softwaretoda
la capacidad que le es superpuesta
por Programación.
- Un Sistema Operativo es un conjunto de programas
que permiten la operación continua de un equipo de computación
y el aprovechamiento de todos sus recursos, entre ellos la memoria
y los medios de Entrada/Salida.
- Controlar los medios de comunicación directa con los usuarios: Terminales (teclado y pantalla), Impresoras, Ratones, Lectoras/Perforadoras de tarjetas y cintas, etc.
- Controlar los medios de almacenamiento secundario: Discos, Disquetes, Cintas, Casetes, etc,. con organización de archivos y directorios. Efectuar las funciones de creación y mantenimiento de archivos y directoris (crear, copiar o mover, renombrar, eliminar).
- Disponer la ejecución de programas haciendo las asignaciones necesarias de recursos del equipo. Esto incluye la ejecución de Ensambladores, Compiladores, Interpretadores.
Entre las tareas típicas de un Sistema
Operativo están:
Si un computador viniera sin ningún
sistema operativo, estaríamos en una situación análoga
a la de un náufrago en una isla desierta: todo tendríamos
que construírnoslo con los recursos existentes en su forma natural
y con nuestro propio trabajo. Generalmente el fabricante suministra junto
con el equipo un sistema operativo especialmente diseñado para ese
equipo o para una familia de equipos similares. A los sistemas operativos
de fabricante se les llama en general sistemas propietarios, como son los
sistemas MVS y OS/400 de IBM.
A partir de los 80s, aparecieron sistemas operativos producidos por productores independientes de software para uso compatible por equipos producidos por diversos fabricantes. Hasta ahora los sistema operativos de tipo standard son: MS DOS, Windows NT para microcomputadores tipo IBM-PC compatibles, UNIX para diversos tipos y capacidades de computadores.
En la mayoría de los sistemas operativos la comunicación con los usuarios se establece a traves de un lenguaje de comandos propio del sistema. Sistemas operativos avanzados, como el Finder de Macintosh o Windows NT proporcionan interfaces gráficas con despliegue de menúes y cuadros de diálogos. Una solución intermedia a los sistemas operados por comandos han sido las interfaces gráficas de usuario, como las versiones de Windows anteriores a NT para PC que adicionalmente expanden la capacidad de trabajo del sistema DOS subyacente, o las interfaces para UNIX basadas en el sistema X-Window.
- Los lenguajes de programación son
lenguajes diseñados para programar: preparar cuerpos de instrucciones
según los diseños de algoritmos para que un computador pueda
ejecutarlos.
- Compilación: Se construye para cada lenguaje, tipo de equipo y/o sistema operativo, programas llamados Compiladores que se encargan de traducir el programa escrito en el lenguaje de alto nivel al lenguaje binario del procesador.Ejemplos: FORTRAN, COBOL, PL1, TURBOPascal, C, C++.
- Interpretación: Se construye para cada lenguaje y generalmente también para cada tipo de equipo y/o sistema operativo, programas llamados Interpretadores o intérpretes que no pretenden traducir hasta lenguaje de máquina sino que traen incorporadas, por programación, la implementación de la funcionalidad del lenguaje de alto nivel.Ejemplos: BASIC, dBASE.
- Mixto: Se utiliza un nivel intermedio de Máquina Virtual, definida por un Repertorio de Instrucciones (Instruction Set) que es implementado en cada tipo de Computador/sistem operativo por Programación de bajo nivel. Para el lenguaje de alto nivel se construye un Compilador al lenguaje de la Máquina Virtual. Esta estrategia fué introducida por N. Wirth (lenguaje P0) para la implementación del Pascal con el objetivo de lograr alta portabilidad, es decir, facilidad para ejecutar el mismo programa en distintos tipos de computadores. Recientemente [1992] Sun Microsystems introdujo el lenguaje Java, basado en esta estrategia, sobre la máquina virtual Java definida por la misma empresa.
- Precompilación: Es similar a la estrategia mixta, pero en vez de compilarse al lenguaje de alguna máquina virtual, se pre-compila a otro lenguaje. El lenguaje objetivo es de nivel inferior en el sentido de que no posee las facilidades de más alto nivel propias del lenguaje precompilado, las cuales son incorporadas directamente y/o mediante bibliotecas de procedimientos. El resultado de la precompilación es un programa expresado en el lenguaje objetivo, el cual a su vez se compila aprovechando el compilador de éste. Debido a la popularización en muchas plataformas del lenguaje C, éste es usado con frecuencia como lenguaje objetivo. Ejemplos: lenguajes de Bases de Datos embebidos en C en los SMBD Informix, DB2; el lenguaje 4GL de Informix usa la estrategia en dos niveles, primero a ESQL (embebido en C) y de éste a C; GNU Pascal, versión para Unix del ObjectPascal a GNU C; GLIDER usa como lenguaje objetivo TurboPascal en la versión DOS, SPARC Pascal en la versión Sun/Solaris y ObjectPascal en la versión Windows 95/NT.
Se distinguen dos tipos generales de lenguajes
de programación: de Bajo nivel y de Alto nivel.
Los lenguajes de Bajo nivel se caracterizan
por ser muy cercanos a los lenguajes propios de las máquinas
y se los llama en general Ensambladores (Assemblers). También
se llaman así a los programas encargados de traducir programas
escritos por los usuarios en lenguaje ensamblador al lenguaje binario de
la máquina. Por lenguaje
propio de la máquina entendemos en lenguaje imperativo que utiliza
solamente instrucciones del repertorio propio de la máquina.
Los lenguajes de Alto nivel, por el contrario, se caracterizan por tratar de ser más bien cercanos al lenguaje matemático ordinario e inclusive algunos pretenden ser cercanos a lenguajes de habla natural.
En general los programas escritos en lenguaje
de alto nivel no pueden ser ejecutados directamente por el CPU. Hay varias
estrategias de programación al problema de ejecutar esos programas:
Note sin embargo que el
lenguaje en sí no determina si el problema de ejecución se
resuelve por alguna de estas vías. Así existen versiones
de BASIC y dBASE compilados o de Pascal interpretado o precomplilado.
Otra distinción que se hace es entre lenguajes de propósito general y lenguajes orientados al problema.Los lenguajes orientados a problemas proporcionan a sus usuarios facilidades adicionales para el desarrollo de aplicaciones de tipo especializado. COBOL es un lenguaje orientado al desarrollo de aplicaciones para empresas, SIMULA, GPSS, GLIDER entre otros son lenguajes de Simulación de Sistemas. MAPLE es un lenguaje orientado a la resolución de problemas matemáticos. SQL y dBASE son lenguajes orientados a Bases de Datos. PL1, Pascal y ObjectPascal, C y C++ son lenguajes de propósito general.
Se llama Programa Fuente al programa en su versión original escrita en el lenguaje de programación. A la versión compilada al lenguaje de máquina pero no necesariamente lista para ejecución se la llama Programa Objeto y a la versión lista para ejecución Programa Ejecutable
En los computadores actuales se utilizan principalmente dos sistemas de codificación de caracteres:
- ASCII: American Standard Code
- EBCDIC: Extended Binary Coded Decimal Interchange Code
Como los textos pueden incluír información numérica, es necesaria la representación en caracteres de los números, pero para efectuar operaciones propiamente numéricas de cálculo se requiere que los operandos numéricos estén almacenados en memoria en representaación numérica binaria. El Apéndice B describe el Sistema de Numeración Binario que es el que se aplica para la representación interna de números para procesamiento numérico.
En el sistema EBCDIC la letra mayúscula "A" se codifica 11000001, la "B" 11000010, la "C" 11000011 y así sucesivamente. El dígito "0" se codifica 11110000, el "1" 11110001, el "2" 11110010, etc.
Una banda o string de caracteres se almacena en la memoria
en bytes consecutivos. La palabra "CASA" se representaría en memoria
así:
| 11000011 | 11000001 | 11100010 | 11000001 |
| C | A | S | A |
En el sistema ASCII la letra mayúscula "A" se codifica 01000001, la "B" 01000010, la "C" 01000011 y así sucesivamente. El dígito "0" se codifica 00110000, el "1" 00110001, el "2" 00110010, etc.
La palabra "CASA" se representaría en memoria así:
| 01000011 | 01000001 | 01100010 | 01000001 |
| C | A | S | A |
El sistema ASCII es el más usado actualmente en microcomputadores y estaciones de trabajo. En manuales de uso de equipos y lenguajes se pude hallar la tabla completa de la codificación ASCII.
Si se interpretan los códigos como números del Sistema Binario de Numeración (Ver Apéndice B), es posible comparar caracteres. Observe que en sistema EBCDIC las letras mayúsculas son menores que los dígitos mientras que en el sistema ASCII ocurre lo contrario.
El orden en el diseño de la codificación permite que sea posible para un computador realizar procesos como ordenación alfabética o búsqueda de palabras en un texto almacenado.
Los contenidos de memorias, pricipal o secundarias, son en definitiva secuencias de bytes cada uno conteniendo una de las 256 configuraciones posibles. El proceso de ejecución determina la interpretación de los contenidos ya sea como instrucciones de programa, datos numéricos o alfanuméricos. Hay ocasiones en que un usuario necesita revisar o asignar contenido de memoria directamente en binario, lo cual es bastante incómodo por tratarse de largas hileras de 0´s y 1´s. En esos casos es conveniente abreviar los contenidos de memoria usando representaciones numéricas de base múltiplo de la base 2 binaria. Las bases múltiplo de 2 más frecuentemente usadas por los computistas y manuales de documentación son la 16 -hexadecimal- y la 8 -octal.
Notación Hedadecimal
Consideremos los 8 bits del byte en dos porciones de 4 bits. Con 4 bits se tienen 16 configuraciones distintas. Las podemos designar para abreviar con los dígitos del 0 al 9 y las letras de la A a la F así:
0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100
= 4 0101 = 5 0110 = 6 0111 = 7
1000 = 8 1001 = 9 1010 = A 1011 = B 1100
= C 1101 = D 1110 = E 0111 = F
Con esta notación se define un sistema de numeración
en base 16 porque se usan 16 símbolos, el
sistema de numeración Hexadecimal. Para formar números,
los símbolos que son dígitos mantienen su valor decimal y
a las letras de la A a la F se las hace valer los valores sucesivos del
10 al 15.
Ejemplo: El valor decimal del número escrito en hexadecimal 7A3F es:
7*163 + (10)*162 + 3*161 + (15)*160 = ((7*16 + 10)*16 + 3)*16 + 15 = 31295
Teorema Fundamental de la Numeración
Usando notación hexadecimal se abrevia nuestra escritura
de números binarios y por tanto también la de los códigos
EBCDIC y ASCII. Por ejemplo, los códigos EBCDIC para las letras
mayúsculas "A",
"B" y "C" se abrevian en hexadecimal como C1, C2 y C3, respectivamente.
Los códigos de los dígitos en EBCDIC se abrevian F0, F1,
..., F9.
Veamos en detalle el caso de la letra "A":
- Su código EBCDIC en binario es: 11000001
Formemos las dos porciones de 4 bits: 1100 y 0001
El primer grupo corresponde a la configuración hexadecimal que designamos como C
El segundo grupo corresponde a la configuración que designamos por su valor 1
Entonces, juntando las dos abreviaciones queda C1
Calculando en binario:
(((((((1*2) + 1)*2 + 0)*2 +0)*2 + 0)*2 + 0)* 2 + 0)* 2 + 1 = 193
Notación Octal
Análogamente se define la notación Octal agrupando bits en grupos de a 3. Con tres bits se tienen las siguientes ocho configuraciones distintas y sus valores:
000 = 0 001 = 1 010 = 2 011 = 3 100 = 4 101 = 5 110 = 6 111 = 7
Usando la notación octal para abreviar códigos de 8 bits, se agrupan los bits de derecha a izquierda considerando un 0 adicional a la izquierda.
Veamos en detalle el caso de la letra "A":
- Su código ASCII en binario es: 01000001
Formemos las dos porciones de 3 bits: 001 000 y 001
El primer grupo corresponde a la configuración octal con valor 1
El segundo grupo corresponde a la configuración con valor 0
El tercer grupo corresponde a la configuración con valor 1
Entonces, juntando las tres abreviaciones queda en octal 101
(1)*82 + 0*8 + 1 = 64 + 0 +1 = 65
Calculando en binario:
(((((((0*2) + 1)*2 + 0)*2 +0)*2 + 0)*2 + 0)* 2 + 0)* 2 + 1 = 65
Apéndice B: Sistema de Numeración Binario
Estamos habituados desde la escuela primaria a usar el sistema de representación numérica Decimal o simplemente sistema decimal, llamado así porque se basa en el uso de 10 símbolos: los dígitos del 0 al 9. Para la formación de números se aplica el gran invento de la antigüedad: la notación posicional.
Teorema Fundamental de la Numeración
Así, por ejemplo, leemos el número 352 como Tres Cientos Cincuenta y Dos, que en símbolos matemáticos equivale a:
3*100 + 5*10 + 2 = 3*102 + 5*101 + 2*100
Esto es:
- Numeramos las posiciones de los dígitos de derecha a izquierda partiendo de 0
- Calculamos el valor posicional del dígito en cada posición: su valor como dígito multiplicado por el valor de la base (10) elevada a la potencia del valor del número de la posición
- El valor total del número es la suma de los valores posicionales de los dígitos
Con las mismas reglas se pueden idear distintos sistemas de numeración eligiendo distintos números de símbolos como base. De hecho, la humanidad en distintas culturas ha usado distintos sistemas como el sexagecimal en base 60 -del cual nos queda herencia en el sistema horario- en base 20, en base 5.
El sistema de numeración Binario de base 2 ha resultado el más conveniente para usar en Computación por la relativa facilidad para distinguir dos configuraciones en diveros medios eléctricos, electrónicos o electromagnéticos.
El sistema binario de numeración utiliza dos símbolos: 0 y 1. Hasta 1 se cuenta igual que en decimal: 0 significa ninguna cantidad, 1 una unidad. El decimal 2, base binaria, se escribe en binario: 10. Note que la base de cualquier sistema de numeración siempre se escribe como 10 en la propia base. Para distinguir cuando pueda haber ambigüedad y tomando como referencia la base 10, podemos usar la siguiente notación con subíndices para la base:
(10)2 = (1*21 + 0*20)10 = (2 + 0)10 = (2)10
donde los subíndices en decimal denotan el valor decimal de la base considerada.
Para calcular el valor decimal de un número en notación binaria -como en cualquier otra notación- aplicacamos la regla del valor posicional. Por ejemplo, calculemos el valor decimal del número binario 10100110.
Teorema Fundamental de la Numeración
Numeremos las posiciones: 1 0
1 0 0 1 1 0
7 6 5 4 3 2 1 0
Sumemos los valores de cada posición:
1*27 + 0*26 +1*25 + 0*24 +0*23 + 1*22 + 1*21 + 0*20
= ((((((1*2 + 0)*2 + 1)*2 + 0)*2 + 0)*2 + 1)*2 + 1)*2 + 0 = 166
Ejercicio: Hallar un algoritmo para efectuar la conversión inversa, de decimal a binario
Ejemplo de suma:
(11011)2 = (27)10 +
+ (00101)2 = ( 5)10
_________ = ______
(100000)2 = (32)10
La representación de números
menores que uno, números fraccionarios, es también análoga
a la decimal. Por ejemplo, el número (0.5)10 decimal
es (0.1)2 binario, pues:
(0.5)10 = 5*10-1
y (0.1)2 = 1*2-1
A la derecha del punto se consideran las potencias negativas sucesivas de la base a partir de -1, es decir, el valor posicional de cada símbolo movido una posición a la derecha del punto equivale a dividir su valor por el valor de la base.
Ejemplo: valor decimal de (101.1011)2
= 1*22 + 0*21 + 1*20
+ 1*2-1 + 0*2-2 + 1*2-3 + 1*2-4
->
<-
= ((1*2 + 0)*2 +1) + (((1/2 +1)/2 + 0)/2
+1)/2
= 5.6875
Se puede normalizar la representación de números <> 0, cualquiera sea la base y el signo, usando dos componentes: una mantisa y un exponente. Con la mantisa se representa el valor absoluto del número multiplicado por una potencia de la base para reducirlo a un rango fijo y con el exponente se ajusta el valor de la potencia de la base para que, multiplicada por la mantisa, reconstruya el valor numérico absoluto original.
Por ejemplo, supongamos que la convención en decimal -como en la notación llamada científica en muchas calculadoras- es que la mantisa sea un valor m tal que: 1 <= m < 10 y queremos representar el número 58736.629. La mantisa sería 5.8736629 y el exponente 4. El número se reconstruye como: 5.8736629 * 104. Si se trata de números menores que 1, el exponente será negativo. La representación de los números: 58736.629, 0.0058736629 y 5.8736629 tiene en los tres casos el mismo valor de mantisa 5.8736629 pero los valores del exponente serán 4, -3 y 0 respectivamente. El efecto del exponente es indicar la posición del punto que separa la parte entera de la parte fracionaria, razón por la cual a este tipo de notación se la llama de punto o coma flotante. Para números negativos, el signo - precede a la mantisa.
Una representación similar a la aquí descrita, binaria de punto flotante, es la que se utiliza en los computadores para representar números con parte fraccionaria llamados en algunos lenguajes impropiamente reales.Sabemos que a fijar el número de cifras significativas con las que se efectúan cálculos, lo que hacemos es trabajar con aproximaciones racionales. Mientras más cifras significativas se usen -manualmente o con computador- mayor será la precisión de los resultados. La ventaja de la representación de punto flotante en calculadoras y computadoras es que permite almacenar un número fijo de dígitos significativos para mayor precisión de las operaciones aritméticas elementales.
En una representación análoga
utilizando el sistema binario de numeración, tanto la mantisa
como el exponente se representan en binario. La convención
del rango de la mantisa m suele ser:
(0.1)2 <= m < 1
Por ejemplo, el número (0.5)10 x 100 en decimal es (0.1)2 x 20 en binario, las bases de los exponentes están escritos ambos en decimal.
El número 5.625 lo podemos escribir
en notación científica como 0.5625 x 101, en decimal
y en binario como (0.101101)2 x (10)2(11)2
es decir, con mantisa (0.101101)2 y exponente (11)2.
(Verifíquelo)