 |
La información mas importante
que se consigue en la tabla 1.2.2 es la función polinómica
estimada de tercer grado, la cual es:
Y(estimada)
= 62.61142857 -9.01142857*X + 0.48142857*X*X -0.0076*X*X*X
en que Y es la resistencia y X
es el porcentaje del algodón.
Se puede maximizar esta función
y para hacer esto se calcula la derivada de Y(estimada ) con respecto X.
Luego se iguala la expresión de la derivada a cero
y se obtiene una ecuación cuadrática cuya solución
produce el valor del X para el cual se obtiene máximo de Y(estimada).
Se podrá
verificar que el máximo de la resistencia se produce para X = 28.23
y el valor del máximo es 20.90
|
Conclusión:
La relación ente la resistencia de la
fibra sintética y el porcentaje del algodón se puede
representar por la siguiente función polinómica estimado
de grado tres:
Y(estimada)
= 62.61142857 -9.01142857*X + 0.48142857*X*X -0.0076*X*X*X
El valor de la resistencia de la fibra sintética
crece a medida que aumenta el valor del porcentaje del algodón,
alcanzando su valor máximo de 20.90 cuando el porcentaje del algodón
asume el valor igual a 28.23
Diseño
Bloques aleatorios:
(2.1): Diseño Bloques aleatorios: (balanceado con efectos fijos)
Fuente de datos: Li, J.C.R. Capítulo
14
Hay 6 tratamientos de Variedades y 5 bloques. Este experimento se
hizo en el campo experimental.
Tabulación de datos: por filas como Variedades y por columnas
como bloques;
La variable repuesta es el rendimiento.
Datos:
32.6 41.0 17.9 23.8 19.6
38.4 39.4 37.1 42.8 21.8
65.1 59.9 41.9 36.1 21.1
54.2 46.4 43.6 35.1 43.4
83.7 37.9 69.3 63.8 50.7
77.1 70.8 57.7 51.1 46.5
Tabla 2.1.1: Análisis de varianza para Diseño B. A.
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 9 6529.2027 725.4670 7.14 0.0001
Error 20 2033.4093 101.6705
Corrected Total 29 8562.6120
R-Square C.V. Root MSE Y Mean
0.762525 22.08317 10.083 45.660
Source DF Type I SS Mean Square F Value Pr > F
VARIEDADES 5 4541.6840 908.3368 8.93 0.0001
BLOQUES 4 1987.5187 496.8797 4.89 0.0065
Comentarios:
El Modelo Lineal
del diseño usado en este experimento es:
Yij
= m + ti
+ bj + eij
; i = 1,...,k ;
j = 1,..,n ; t.=
0 ; b.
= 0 ;
en que,
ti
= el efecto del tratamiento
i - ésimo ;
bj
= el efecto del bloque
j - ésimo ;
eij
= error aleatorio para la observación en el j - ésimo
bloque y el tratamiento i - ésimo. eij
~ NID(0, s2
)
;
para (i
= 1,...,k ; j = 1,..,n ;)
Hipótesis
nula y alternante:
H0: ti
= 0 ;
para todo i = 1,...,k; HA:
ti
¹ 0 ; para
algún i ;
H0:
bj
= 0 ;
para todo j = 1,...,n; HA:
bj
¹ 0 ; para
algún j ;
Nota:
Las hipótesis antes especificadas también se pueden enunciar
en términos de promedios de poblaciones de varidades y bloques respectivamente
en una forma similar tal como se hizo en el ejemplo 1.1 .
El valor del
F calculado para variedades es altamente significativo. Por lo tanto
será necesario usar un método del análisis
posterior para determinar cual es la mejor variedad.
El valor del
F calculado para bloques es altamente significativo y esto indica
que se justificó el uso del diseño bloques aleatorios ya
que una parte de la variabilidad total que se particiona en el análisis
de varianza como bloques es significativa. (Si F para bloques en un diseño
bloques aleatorios usado en el campo experimental no es significativo,
entonces diríamos que los bloques no fueron construidos
y ubicados con una orientación correcta.
La orientación correcta consiste en
ubicar los bloques en forma perpendicular a la dirección en
que varía la fertilidad del suelo. El Contraste de hipótesis
acerca de los bloques aún cuando no es de interés directo
para el Investigador, se considera como un paso importante para confirmación
de criterios usado en el planeamiento del experimento.)
Tabla 2.1.2: Análisis posterior por el Método de Duncan:
General Linear Models Procedure
Duncan's Multiple Range Test for variable: Y
NOTE: This test controls the type I comparisonwise error rate,
not the experimentwise error rate
Alpha= 0.05 df= 20 MSE= 101.6705
Number of Means 2 3 4 5 6
Critical Range 13.30 13.96 14.38 14.68 14.89
Means with the same letter are not significantly different.
Duncan Grouping Mean N VARIEDAD
A 61.080 5 5
A
A 60.640 5 6
B 44.820 5 3
B
B 44.540 5 4
B
C B 35.900 5 2
C
C 26.980 5 1
Comentarios:
El uso del Rango múltiple de Duncan produce
tres conjunto disjuntos de variedades. El grupo con el mejor rendimiento
consta de dos variedades que son las variedades números 5 y 6. Cualquiera
de estas dos variedades se pueden usar y entre ellas no existe diferencia
significativa.
(2.2):
Diseño Bloques aleatorios: (no balanceado con efectos fijos)
Hay 3 tratamientos de Variedades y 5 bloques.
Existe un dato faltante que se encuentra en el primer tratamiento y
primer bloque.
Tabulación de datos: por filas como Tratamientos y por
columnas como bloques:
. 887 897 850 975
857 1189 918 968 909
917 1072 975 930 954
Tabla 2.2.1: Diseño B. A. con un dato faltante
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 6 62501.989 10416.998 1.79 0.2316
Error 7 40713.725 5816.246
Corrected Total 13 103215.714
R-Square C.V. Root MSE Y Mean
0.605547 8.029030 76.264 949.86
Source DF Type I SS Mean Square F Value Pr > F
BLOCK 4 42255.048 10563.762 1.82 0.2303
TRAT 2 20246.942 10123.471 1.74 0.2435
Source DF Type III SS Mean Square F Value Pr > F
BLOCK 4 49805.025 12451.256 2.14 0.1785
TRAT 2 20246.942 10123.471 1.74 0.2435
Comentarios:
Este ejemplo
tiene el propósito de ilustrar el procedimiento a usar y los aspectos
computacionales cuando existe(n) dato(s) faltante(s) en un diseño
B. A. con efectos fijos.
Generalmente un diseño B. A. se planifica
como un diseño balanceado pero al perder uno o más datos
experimentales, el diseño llega a ser un diseño no balanceado.
Pueden surgir muchas complicaciones en el análisis estadístico
y pérdidas de propiedades óptimas del diseño por el
no balanceo, por ejemplo: El error estándar de promedios de tratamientos
ya no es un valor constante sino varia según si se trata del promedio
de un tratamiento que tiene el problema de dato(s) faltante(s) o no. Se
pierde la propiedad de ortogonalidad del diseño ya que no se cumplirá
la propiedad que S.C. Total = S.C. Bloques + S.C. Tratamientos + S.C. Error
experimental. En general se reduce la potencia de la dócima
del estadístico F , lo cual pudiera hacer difícil detectar
las diferencias significativas.
En cuanto al procedimiento computacional a usar,
se hace necesario usar Sumas de cuadrados, cuadrados medios y F del
tipo III (Type III ) en la salida del SAS, para ambas fuentes de variación
que serían bloques y tratamientos. En este ejemplo el valor
de F para bloques es 2,14 y el valor de F para tratamientos es 1,74
Diseño Cuadrado
Latino
(3.1): Cuadrado Latino:
4 Filas: 4 Columnas: 4 Tratamientos(Variedades de Trigo) ;
y = Rendimiento por parcela en Kg. ;
Ejemplo: Steel, R.G.D y Torrie, J.H.: Capitulo 8 ;
DATOS:
C 10.5 D 7.7 B 12.0 A 13.2
B 11.1 A 12.0 C 10.3 D 7.5
D 5.8 C 12.2 A 11.2 B 13.7
A 11.6 B 12.3 D 5.9 C 10.2
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 9 87.680000 9.742222 21.49 0.0007
Error 6 2.720000 0.453333
Corrected Total 15 90.400000
R-Square C.V. Root MSE Y Mean
0.969912 6.443065 0.6733 10.450
Source DF Type I SS Mean Square F Value Pr > F
FILAS 3 1.955000 0.651667 1.44 0.3219
COLUMNAS 3 6.800000 2.266667 5.00 0.0452
TRATAMIENTOS 3 78.925000 26.308333 58.03 0.0001
Comentarios:
Considerando
el nivel de significación
a = 0,05,
observamos que el F calculado para Filas no es significativo
mientras el valor de F calculado para columnas es significativo. Esto podría
indicar que ha habido una falla en
el planeamiento del diseño y/o la construcción
de las columnas. Surgen dudas sobre la justificación del diseño
utilizado, ya que se pudo utilizar el diseño bloques aleatorios
para controlar la variabilidad por columnas.
F para tratamientos es altamente significativo.
Por lo tanto, se debe realizar Análisis del Rango Múltiple
de Duncan para determinar el mejor tratamiento. . Se omite este cómputo
aquí, ya que sería similar como se ha hecho esto en ejemplos
anteriores.
(4):
Experimentos Factoriales
(4.1): Experimento Factorial
2x4 en el Diseño B. A.
(4.1):
Experimento Factorial 2x4 en el Diseño B. A.
* Datos: Li, J C. R., Capitulo 18: Introduction to Statistical Inference
* Factores: Fecha de siembra con 2 niveles: Temprana , Tardía ;
* Factor: Abono con 4 niveles: Abono estándar, Aéreo, Na, y, K ;
* Número de bloques = 4 ;
* Variable respuesta: rendimiento por parcela de soya ;
* Tabulación de datos:
* Bloques ;
* Fecha de siembra Abono 1 2 3 4 ;
* Temprana Abono estándar - - - - ;
* Temprana Aéreo - - - - ;
* Temprana Na - - - - ;
* Temprana K - - - - ;
* .... Después siguen 4 lineas siguientes para fecha de siembra tardía ....;
Datos:
28.6 36.8 32.7 32.6
29.1 29.2 30.6 29.1
28.4 27.4 26.0 29.3
29.2 28.2 27.7 32.0
30.3 32.3 31.6 30.9
32.7 30.8 31.0 33.8
30.3 32.7 33.0 33.9
32.7 31.7 31.8 29.4
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 10 94.100000 9.410000 2.97 0.0169
Error 21 66.438750 3.163750
Corrected Total 31 160.538750
R-Square C.V. Root MSE Y Mean
0.586151 5.773807 1.7787 30.806
Source DF Type I SS Mean Square F Value Pr > F
BLOQUE 3 7.306250 2.435417 0.77 0.5238
FECHA 1 32.000000 32.000000 10.11 0.0045
ABONO 3 16.401250 5.467083 1.73 0.1919
FECHA*ABONO 3 38.392500 12.797500 4.05 0.0204
Comentarios:
Usaremos el nivel de significación igual
a 0,05 . Observamos que el valor de F para bloques no es significativo.
Esto indica que hubo una falla en el planeamiento del experimento y/o en
la construcción o orientación de los bloques en el campo
experimental.

La interacción Fecha x Abono es significativa
y en consecuencia no se puede realizar el análisis posterior
entre los promedios de niveles de ninguno de los dos factores. El Análisis
gráfico de esta interacción revela que las líneas
de promedios correspondientes a las fechas de siembra muestran una intersección
indicando que existe una interacción por el cambio en la dirección
de la respuesta. Ya que el factor Abono no es significativo, no necesitamos
hacer ningún análisis posterior entre los promedios de 4
niveles del factor abono. La interacción Fecha
x Abono significativa, implica que la que será
la mejor fecha dependerá del nivel del factor Abono con que esta
se combina. Pero si se puede aplicar cualquier método
del análisis posterior, (por ejemplo Duncan) sobre los 8
promedios de tratamientos formados por todas las combinaciones posibles
entre los 2 niveles del factor Fecha y los 4 niveles del Factor abono.
Tomando en cuenta la información que se
presenta en el cuadro más arriba, podemos hacer diferentes tipos
de comparaciones:
Comparación entre promedios de diferentes
tipos de Abono para la siembra Temprana.
Comparación entre promedios de diferentes
tipos de Abono para la siembra Tardía.
Comparación entre promedios de los dos
tipos de fechas de siembra separadamente para cada tipo de abono.
(No se requiere a volver a hacer otro cómputo
del método de Duncan, sino usar los resultados del Análisis
de Duncan ya disponible)
El tratamiento que tiene el rendimiento más
alto es cuando se combina el Abono estándar
con una siembra temprana.
Diseños
de Parcelas Divididas:
Los datos utilizados en este ejemplo proviene
del libro de Steel, R.G.D. y Torrie, J.H. 4 lotes de semillas de
avena fueron usados como tratamientos principales. Hay 4 sub tratamientos
que consisten en un testigo mas tres productos químicos que sirven
para controlar una enfermedad de plantas. Se usaron 4 bloques.
Este diseño asigna la máxima precisión
de estimación al factor productos químicos (Sub Tratamientos)
y la mínima precisión a al factor Lotes de semillas(Tratamiento
principal).
Tabulación de datos:
Los datos se muestran en el programa de SAS.
Las primeras 4 filas de datos corresponden a los datos de los bloques 1
- 4, para el primer nivel del Tratamiento principal. Dentro de cada fila
hay 4 datos correspondientes a los 4 niveles de sub tratamientos.
Las próximas 4 filas de datos corresponden
a los datos de los bloques 1 - 4, para el segundo nivel del Tratamiento
principal. Dentro de cada fila hay 4 datos correspondientes a los 4 niveles
de sub tratamientos.
etc. y así sucesivamente hasta la tabulación
de las últimas 4 filas correspondientes al cuarto y último
nivel del Tratamiento principal.
Programa fuente SAS:
data pdivid ;
do tratprin = 1 to 4;
do bloques = 1 to 4;
do subtrat = 1 to 4;
input Y @;
output;
end;
input;
end;
end;
cards;
42.9 53.8
49.5 44.4
41.6 58.5
53.8 41.8
28.9 43.9
40.7 28.3
30.8 46.3
39.4 34.7
53.3 57.6
59.8 64.1
69.6 69.6
65.8 57.4
45.4 42.4
41.4 44.1
35.1 51.9
45.4 51.6
62.3 63.4
64.5 63.6
58.5 50.4
46.1 56.1
44.6 45.0
62.6 52.7
50.3 46.7
50.3 51.8
75.4 70.3
68.8 71.6
65.6 67.3
65.3 69.4
54.0 57.6
45.6 56.6
52.7 58.5
51.0 47.4
;
proc print; run;
proc GLM;
class Bloques Tratprin Subtrat;
model Y = Bloques Tratprin Bloques*Tratprin
Subtrat Tratprin*Subtrat /ss1 ;
test h= Bloques Tratprin e=Tratprin*Bloques;
means Tratprin subtrat Tratprin*subtrat;
title 'Diseño Parcela Dividida';
run;
Salida SAS:
Nota:
La salida SAS, tal como imprime el computador
no se puede usar, sino será necesario reordenar la información
obtenida en una tabla de Andeva definitiva.
Esta tabla que se obtenga, se llamará como tabla de andeva del diseño
de parcelas divididas, sin usar el calificativo "definitiva". Se usa este
calificativo "definitiva" simplemente para indicar que hay un trabajo que
hacer y una vez que este trabajo esta hecho, se obtendrá la tabla
de andeva, la que se va a usar. Esta tabla se muestra después
de la salida SAS, la cual lleva algunas indicaciones en color rojo para
preparar la tabla de Andeva definitiva:
Diseño Parcela Dividida
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 27 7066.1919 261.7108 12.89 0.0001
Error 36 731.2025 20.3112 Nombrarla como Error(b)
Corrected Total 63 7797.3944
R-Square C.V. Root MSE Y Mean
0.906225 8.534077 4.5068 52.809
Source DF Type I SS Mean Square F Value Pr > F
BLOQUES 3 2842.8731 947.6244 46.66 0.0001 No usar esta Fila.
TRATPRIN 3 2848.0219 949.3406 46.74 0.0001 No usar esta Fila.
BLOQUES*TRATPRIN 9 618.2944 68.6994 3.38 0.0042 Nombrarla como Error(a)
SUBTRAT 3 170.5369 56.8456 2.80 0.0539
TRATPRIN*SUBTRAT 9 586.4656 65.1628 3.21 0.0059
Tests of Hypotheses using the Type I MS for
BLOQUES*TRATPRIN as an error term
Source DF Type I SS Mean Square F Value Pr > F
BLOQUES 3 2842.8731 947.6244 13.79 0.0010 Usar esta Fila.
TRATPRIN 3 2848.0219 949.3406 13.82 0.0010 Usar esta Fila.
A
continuación se muestra la Tabla de Andeva definitiva.
Análisis de Varianza
Fuentes de Variación G.L. S.C. C.M. F Pr > F
BLOQUES 3 2842.8731 947.6244 13.79 0.0010
TRATPRIN 3 2848.0219 949.3406 13.82 0.0010
Error(a) 9 618.2944 68.6994
SUBTRAT 3 170.5369 56.8456 2.80 0.0539
TRATPRIN*SUBTRAT 9 586.4656 65.1628 3.21 0.0059
Error(b) 36 731.2025 20.3112
Corrected Total 63 7797.3944
Comentarios:
Consideraremos
el nivel de significación a
= 0,05.
F para bloques es significativo y esto indica
que hubo justificación en usar bloques en el diseño para
controlar la variabilidad.
Tratprin es la abreviatura para Tratamientos
principales y tiene el valor de F significativo, lo cual implica que hay
diferencias significativas entre los promedios poblacionales de los 4 lotes
de semillas de avena.
La fuente de variación Sub tratamientos
no tiene el valor de F significativo y esto señala que no existen
diferencias significativas entre los promedios poblacionales de los 4 productos
químicos.
La interacción tratamientos principal*subtratamientos
es significativa lo cual indica que el mejor lote de semilla de avena
podría ser diferente para los diferentes productos químicos
usados. También observamos que debido a la presencia de la interacción
significativa no podemos aplicar el método del análisis posterior
a los promedios de los 4 lotes de semillas de avena sino que los mismos
deben ser comparados separadamente por cada uno de 4 productos químicos
y así también podemos comparar las 16 combinaciones de tratamientos.
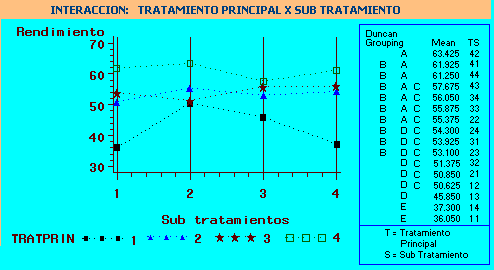
Análisis Gráfico:
En la gráfica de la interacción
Tratamiento Principal x Sub tratamiento, se observa la presencia de una
interacción por el cambio en la dirección de la respuesta,
ya que las líneas, correspondientes a los tratamientos principales,
muestran puntos de intersección.
La línea de promedios correspondiente
al Tratamiento principal número 4, siempre se encuentra arriba de
las otras tres líneas restantes. Por lo tanto, el mejor tratamiento
principal, debería ser el cuarto, sujeto a confirmación del
resultado del Análisis de Duncan
Análisis de Duncan:
Ya que la interacción Tratamiento Principal
x Sub Tratamiento es significativa, no podemos realizar análisis
posterior sobre los promedios de Tratamientos principales y asimismo
tampoco sobre los promedios de Sub Tratamientos (además este último
es no significativo). Se puede hacer la comparación entre los 16
tratamientos combinaciones por el Análisis de Duncan y el resultado
de este procedimiento podrá ser usado para responder preguntas inicialmente
planteadas en el objetivo del experimento.
Para realizar el cómputo del método
de Duncan, es necesario obtener un estimación del error experimental,
la cual se puede hallar por el promedio ponderado de los cuadrados medios
de los dos errores (a) y (b) en el diseño. En este ejemplo, esta
estimación mancomunada tendrá 45 g.l.
El Análisis de Duncan revela que el
mejor tratamiento es la combinación 42. También se ha formado
otro grupo que contiene las combinaciones de tratamientos: 14 y 11, que
tiene los promedios más bajos para la variable respuesta rendimiento.
Utilizando los resultados del del Análisis
de Duncan, también se puede determinar: (No
se requiere a volver a hacer otro cómputo del método de Duncan,
sino usar los resultados del Análisis de Duncan ya disponible.)
(a): el mejor subtratamiento para cada
uno de los tratamientos principales separadamente.
(b): el mejor Tratamiento Principal
para cada uno de los Subtratamientos separadamente.
|
(6):
Diseño de Parcelas Sub Divididas
Los datos utilizados en este ejemplo proviene
del libro de Montgomery, D. Se trata de una investigación
médica para estudiar el tiempo de absorción de un cierto
tipo de cápsula antibiótica. En esta investigación
se utilizaron 3 técnicos como Tratamientos principales, 3 dosis
como Sub Tratamientos y 4 niveles de grosor de la pared de cápsula
como Sub Sub Tratamientos. El experimento se hizo en 4 bloques.
Este diseño asigna la máxima precisión
de estimación al factor grosor (Sub Sub Tratamientos) , la mediana
precisión al factor dosis (Sub Tratamientos) y la mínima
precisión al factor técnico (Tratamiento principal).
Tabulación de datos:
El esquema de la tabulación de datos se presenta a continuación.
Los datos se muestran en el programa de SAS.
Técnico
-----------------------------------------------------
1
2
3
-----------------------------------------------------
Bloques Dosis
1 2 3 1
2 3 1 2
3
-----------------------------------------------------
Grosor - - -
- - - -
- -
1 - -
- - -
- - - -
1
2 - -
- - -
- - - -
3 - -
- - -
- - - -
4 - -
- - -
- - - -
- indica un dato. Cada
fila tiene 9 datos. Este esquema se repite para los 3 bloques restantes.
Programa fuente SAS:
title Parcelas sub divididas;
data psubdiv ;
do Bloques = 1 to 4;
do Grosor = 1 to 4;
do Tecnico = 1 to 3;
do dosis = 1 to 3 ;
input y @@;
output;
end;
end;
input;
end;
end;
cards;
95 71 108 96 70 108 95 70 100
104 82 115 99 84 100 102 81 106
101 85 117 95 83 105 105 84 113
108 85 116 97 85 109 107 87 115
95 78 110 100 72 104 92 69 101
106 84 109 101 79 102 100 76 104
103 86 116 99 80 108 101 80 109
109 84 110 112 86 109 108 86 113
96 70 107 94 66 100 90 73 98
105 81 106 100 84 101 97 75 100
106 88 112 104 87 109 100 82 104
113 90 117 121 90 117 110 91 112
90 68 109 98 68 106 98 72 101
100 84 112 102 81 103 102 78 105
102 85 115 100 85 110 105 80 110
114 88 118 118 85 116 110 95 120
;
proc print; run;
PROC GLM;
class Bloques Tecnico Dosis Grosor ;
model y = bloques tecnico bloques*tecnico dosis tecnico*dosis dosis*bloques(tecnico)
grosor tecnico*grosor dosis*grosor tecnico*dosis*grosor/ss1 ;
test h=bloques tecnico e=bloques*tecnico;
test h=dosis tecnico*dosis e=dosis*bloques(tecnico);
Run;
Salida SAS:
Parcelas subdivididas
General Linear Models Procedure
Dependent Variable: Y
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 62 25921.472 418.088 46.83 0.0001
Error 81 723.188 8.928 Nombrar esta F.V. como Error(c)
Corrected Total 143 26644.660
R-Square C.V. Root MSE Y Mean
0.972858 3.074926 2.9880 97.174
Source DF Type I SS Mean Square F Value Pr > F
BLOQUES 3 48.410 16.137 1.81 0.1524 No usar esta Fila.
TECNICO 2 248.347 124.174 13.91 0.0001 No usar esta Fila.
BLOQUES*TECNICO 6 161.153 26.859 3.01 0.0105 Nombrarla como Error(a)
DOSIS 2 20570.056 10285.028 1151.97 0.0001 No usar esta Fila.
TECNICO*DOSIS 4 125.944 31.486 3.53 0.0105 No usar esta Fila.
BLOQUE*DOSIS(TECNIC) 18 226.000 12.556 1.41 0.1514 Nombrarla como Error(b)
GROSOR 3 3806.910 1268.970 142.13 0.0001
TECNICO*GROSOR 6 126.486 21.081 2.36 0.0375
DOSIS*GROSOR 6 402.278 67.046 7.51 0.0001
TECNICO*DOSIS*GROSOR 12 205.889 17.157 1.92 0.0435
Tests of Hypotheses using the Type I MS for
BLOQUES*TECNICO as an error term
Source DF Type I SS Mean Square F Value Pr > F
BLOQUES 3 48.40972 16.13657 0.60 0.6378
TECNICO 2 248.34722 124.17361 4.62 0.0609
Tests of Hypotheses using the Type I MS for
BLOQUE*DOSIS(TECNIC) as an error term
Source DF Type I SS Mean Square F Value Pr > F
DOSIS 2 20570.056 10285.028 819.16 0.0001
TECNICO*DOSIS 4 125.944 31.486 2.51 0.0784
A continuación se muestra la Tabla de Andeva definitiva.
Análisis de Varianza
Fuentes de Variación G.L. S.C. C.M. F Pr > F
BLOQUES 3 48.40972 16.13657 0.60 0.6378
TECNICO 2 248.34722 124.17361 4.62 0.0609
Error(a) 6 161.153 26.859
DOSIS 2 20570.056 10285.028 819.16 0.0001
TECNICO*DOSIS 4 125.944 31.486 2.51 0.0784
Error(b) 18 226.000 12.556
GROSOR 3 3806.910 1268.970 142.13 0.0001
TECNICO*GROSOR 6 126.486 21.081 2.36 0.0375
DOSIS*GROSOR 6 402.278 67.046 7.51 0.0001
TECNICO*DOSIS*GROSOR 12 205.889 17.157 1.92 0.0435
Error(c) 81 723.188 8.928
Corrected Total 143 26644.660
Comentarios:
El valor de F para Técnico no es significativo.
Esto indica que los tres Técnicos han tenido éxito en conducir
el experimento de una manera uniforme. Puesto que F para dosis es significativo,
podemos concluir que existen diferencias significativas entre las potencias
de las 3 dosis que se han probado en este experimento. La interacción
Técnico*Dosis al no ser significativa, asegura que las 3 dosis entre
ellas mantienen las mismas diferencias relativas del tiempo de absorción
, no importa cual es el Técnico quién lo prepara. Esta información
es importante ya que esto asegura la uniformidad en la calidad del producto
elaborado.
Grosor es significativo, lo cual implica que
la potencia del antibiótico depende del grosor de la pared de cápsula.
La interacción DOSIS*GROSOR es significativa. Esto indica
que el factor dosis y el factor grosor de la cápsula no son
independientes. La interacción TECNICO*GROSOR es significativa indicando
que el nivel del factor grosor que tenga el mejor tiempo de absorción
depende del técnico quién ha elaborado el antibiótico.
La interacción triple Tecnico*Dosis* Grosor, por ser una interacción
de tres factores puede ser causada de una manera compleja por la significación
de cualesquiera de las siguientes interacciones: Técnico por
Dosis*Grosor, o Dosis por Técnico*Grosor o por Grosor por
Técnico*Dosis.
A continuación se presenta la información
necesaria para hacer el Análisis gráfico de las 3 interacciones
dobles:



